Сводка и группировка, средние величины, показатели вариации. Индексы

Контрольная работа по теории статистики.

Вариант № 4.

Тема 1. Сводка и группировка, средние величины, показатели вариации.

Задача 1.

Рабочие фирмы по производству пластиковых окон характеризуются следующими показателями:

1.  Используя комбинацию признаков, проведите группировку рабочих по стажу работы, определив оптимальное число групп самостоятельно;

2.  Построить гистограмму, полигон распределения работников по стажу работы, а также кумуляту;

3.  Определите структурные средние стажа работы представленного ряда;

4.   Выполните аналитическую группировку для выявления связи между стажем работы и средней выработкой каждой группы.

Решение.

1.  Проведем группировку рабочих по стажу работы, распределив объекты совокупности по пяти группам.

Для построения ряда распределения с пятью равными интервалами необходимо вычислить длину интервала I:

, где X_max – максимальное значение признака,

                               X_min – минимальное значение признака,

                                     n – число интервалов.

X_max = 26, X_min = 0, n = 5, отсюда I =  = 5,2

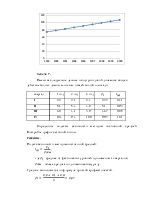
Следовательно, ряд распределения работников по стажу работы  примет вид:

Частоты интервалов обозначают количество работников в каждой группе.

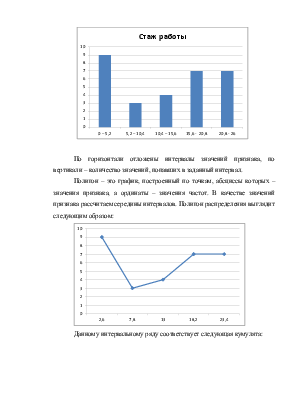
2.  Графической иллюстрацией полученного распределения признака по выбранным интервалам может служить следующая гистограмма:

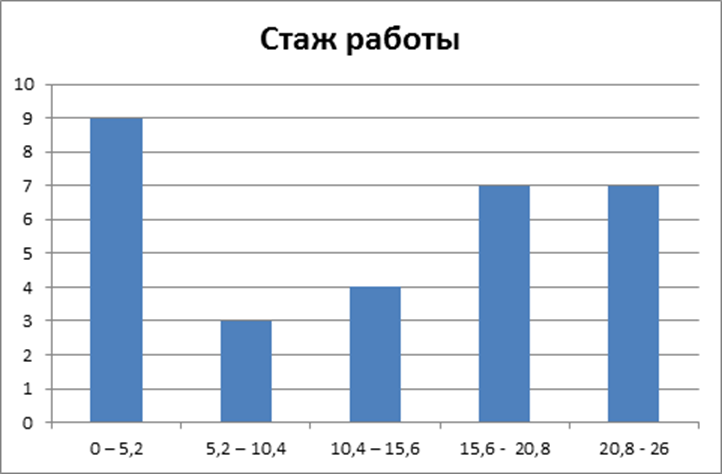
По горизонтали отложены интервалы значений признака, по вертикали – количество значений, попавших в заданный интервал.

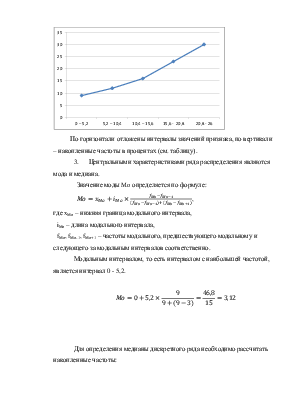
Полигон – это график, построенный по точкам, абсциссы которых – значения признака, а ординаты – значения частот. В качестве значений признака рассчитаем середины интервалов. Полигон распределения выглядит следующим образом:

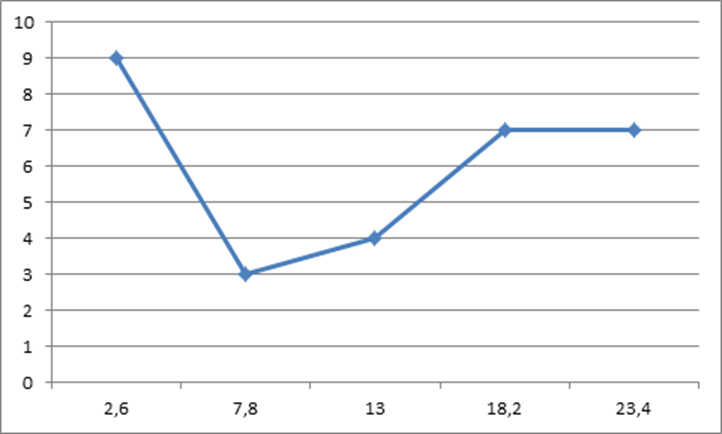
Данному интервальному ряду соответствует следующая кумулята:

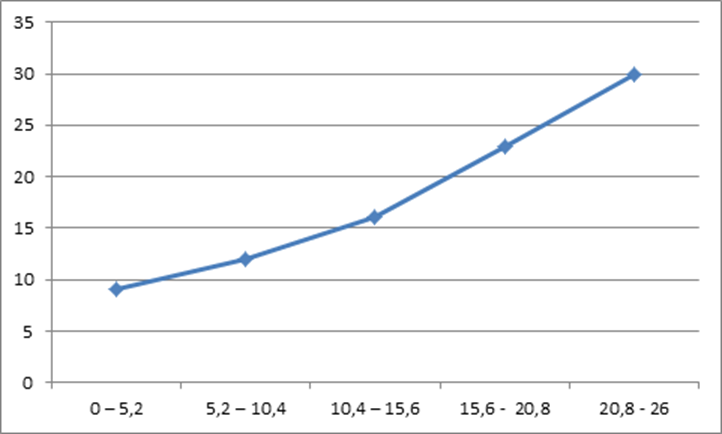
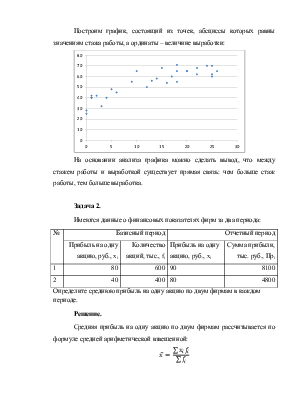
По горизонтали отложены интервалы значений признака, по вертикали – накопленные частоты в процентах (см. таблицу).

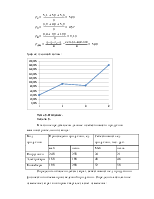
3.   Центральными характеристиками ряда распределения являются мода и медиана.

Значение моды Mo определяется по формуле:

,

где x_Mo – нижняя граница модального интервала,

  i_Mo – длина модального интервала,

  f_Mo, f_Mo-1, f_Mo+1 – частоты модального, предшествующего модальному и следующего за модальным интервалов соответственно.

Модальным интервалом, то есть интервалом с наибольшей частотой, является интервал 0 - 5,2.

Для определения медианы дискретного ряда необходимо рассчитать накопленные частоты:

Из данных таблицы видно, что медианным интервалом является интервал 10,4 – 15,6. 

Медиана Me для интервального ряда определяется по формуле:

,

где x_Me – нижняя граница медианного интервала,

       i_Me – длина медианного интервала,

       Σf – сумма частот интервала,

       cumf_Me-1 – накопленная частота в интервале, предшествующем медианному,

      f _Me – частота медианного интервала.

4.  Проведем аналитическую группировку ряда для выявления связи между стажем работы и выработкой.

Корреляционная решетка – это аналитическая группировкаединиц совокупности по двум признакам, между которыми оценивается связь. Такие группировки необходимо построить для каждого факторного признака с результативным признаком. По расположению и концентрации единиц на поле корреляционной решетки можно сделать предположение о наличии и направлении связи, а также предварительную оценку тесноты связи.