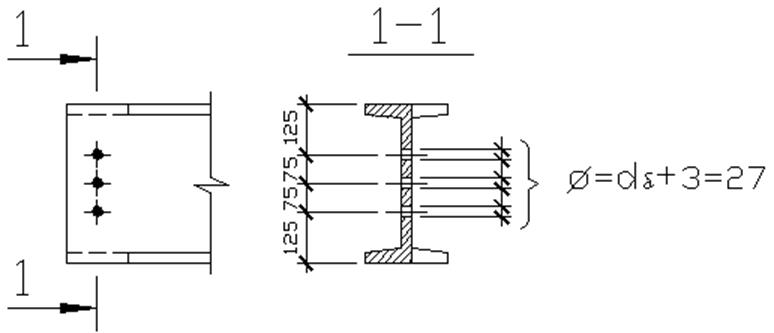
Рис. 12
а б
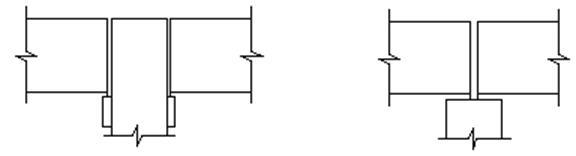
в
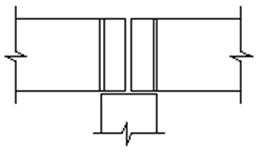
Рис. 13
ПРОВЕРКА УСТОЙЧИВОСТИ БАЛКИ
Общая устойчивость балки проверяется по формуле (1,п.4.17)
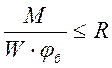
Однако в нашем случае она заведомо обеспечена, так как металлический настил непрерывно уложен на сжатый пояс балки и скреплен с ним сваркой. Аналитическую проверку устойчивости балки в этом случае делать нет необходимости (1, п.4.17,а). Если бы сопряжение балки было этажным, то проверку устойчивости не надо было бы выполнять в соответствии с (1, п.4.17,б).
ПРОВЕРКА МЕСТНОЙ УСТОЙЧИВОСТИ ЭЛЕМЕНТОВ БАЛКИ
Местная устойчивость основных элементов балки – сжатых поясов и стенки – обеспечивается и проверяется по-разному. В поясах достаточно выдержать предельное соотношение
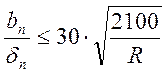 , а
оно учитывается при компоновке поясов, и местная устойчивость их, как сжатых
листов будет обеспечена. В стенках определить просто отношение
, а
оно учитывается при компоновке поясов, и местная устойчивость их, как сжатых
листов будет обеспечена. В стенках определить просто отношение 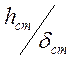 недостаточно, и проверка местной
устойчивости здесь производиться с учетом всех компонентов напряженного
состояния
недостаточно, и проверка местной
устойчивости здесь производиться с учетом всех компонентов напряженного
состояния ![]() (1, п.6.2). Целесообразно проверять
наиболее напряженные отсеки. В нашем случае это отсек ближний к середине
пролета и опорный, совпадающий к тому же с местом изменения сечения. Соответствующие
расчетные отсеки показаны штриховкой на рис. 15. Их срединные сечения имеют
привязки
(1, п.6.2). Целесообразно проверять
наиболее напряженные отсеки. В нашем случае это отсек ближний к середине
пролета и опорный, совпадающий к тому же с местом изменения сечения. Соответствующие
расчетные отсеки показаны штриховкой на рис. 15. Их срединные сечения имеют
привязки ![]() , найденные при теоретической длине пролета
(12 м), без учета фактического укорочения балки на ширину сечения колонны.
, найденные при теоретической длине пролета
(12 м), без учета фактического укорочения балки на ширину сечения колонны.
Проверка
местной устойчивости производится по формуле, учитывающей, что ![]()
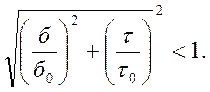
а б
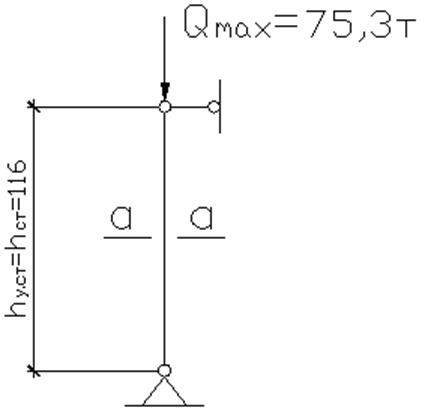
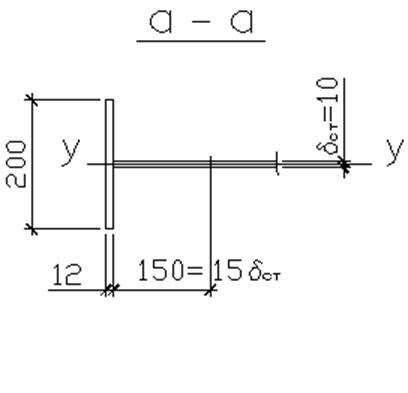
Рис. 14
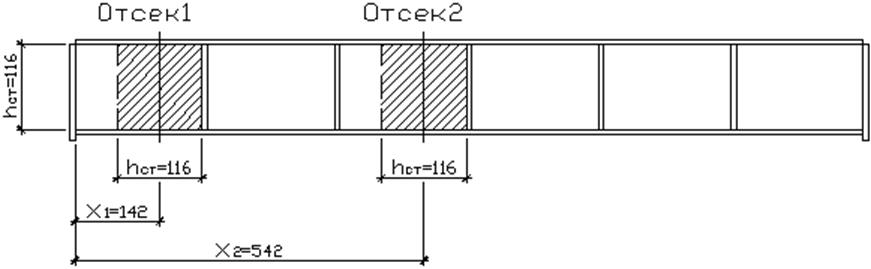
Рис. 15
Найдем критические напряжения, одинаковые для обоих отсеков, имеющих равные размеры.
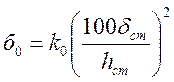 .
.
Для
определения ![]() вычислим
вычислим 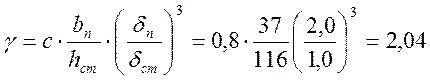 , имея
c=0,8 по табл. 27 (1), а все размеры по рис. 9. По
табл.26 (1) находим
, имея
c=0,8 по табл. 27 (1), а все размеры по рис. 9. По
табл.26 (1) находим ![]() =7,0 при
=7,0 при ![]() ,
тогда
,
тогда
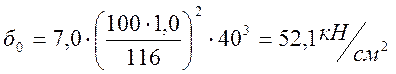 ;
; 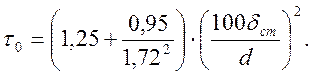 Так как в нашем случае
Так как в нашем случае
d=![]()
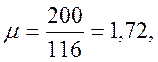 то
то 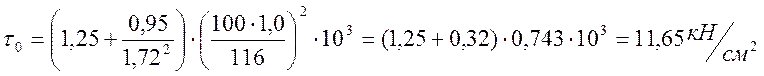 .
.
Вполне очевидно, ![]() , а фактические напряжения
, а фактические напряжения ![]() крайних волокон стенки как в сечении
крайних волокон стенки как в сечении ![]() , так и в сечении
, так и в сечении ![]() меньше
меньше
![]() . Следовательно
. Следовательно 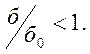 Напряжения
в сечении
Напряжения
в сечении ![]() и составляют
и составляют 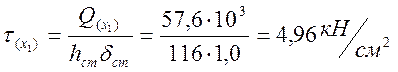 , где
, где
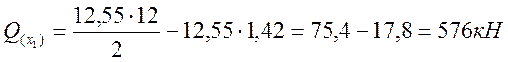 .
.
Так как ![]() то и
то и ![]() следовательно
следовательно
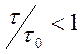 , и проверку по общей формуле делать не
нужно. Можно сделать вывод, что местная устойчивость стенки по всем отсекам
обеспечена.
, и проверку по общей формуле делать не
нужно. Можно сделать вывод, что местная устойчивость стенки по всем отсекам
обеспечена.
Вопрос о
проверке местной устойчивости для балки по рис.15, в клетке по рис.2,а, причем
несколько условно. Как и при размещении ребер жесткости, принято, что ![]() от некоторой распределенной нагрузки
от некоторой распределенной нагрузки ![]() .
.
Содержание этой проверки изменится, если балка по рис.15 будет использована в клетке по рис.2,а при той же распределенной нагрузке и этажном сопряжении. Здесь на главную балку будут опираться балки настила (вспомогательные) с двух сторон, действуя на нее усилием (рис.16,а)
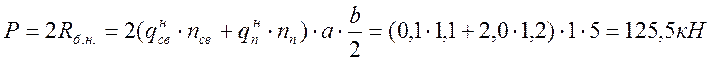 .
.
Так как
высота балки и ее сечение прежние, то, в принципе, можно сохранить принятую
расстановку ребер жесткости с шагом 2м. Но шаг балок настила меньше 1м.
Следовательно ![]() и его необходимо найти,
во-первых, с целью проверки местной прочности стенки (одновременно решив вопрос
о целесообразности постановки дополнительных ребер жесткости), во-вторых, с
целью сравнения их с критическими местными напряжениями, т.к. при
и его необходимо найти,
во-первых, с целью проверки местной прочности стенки (одновременно решив вопрос
о целесообразности постановки дополнительных ребер жесткости), во-вторых, с
целью сравнения их с критическими местными напряжениями, т.к. при ![]() проверка местной устойчивости
производиться по формуле (1, п.6.5)
проверка местной устойчивости
производиться по формуле (1, п.6.5)
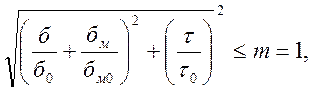 где m-коэффициент условия работы конструкции.
где m-коэффициент условия работы конструкции.
Согласно (1,п.4.13) для обеспечения местной прочности должно быть выполнено условие
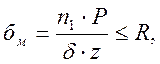 где
где ![]() =1 для всех балок, кроме подкрановых;
=1 для всех балок, кроме подкрановых; ![]() =1 см-толщина стенки; z-условная
длина распределения сосредоточенного давления.
=1 см-толщина стенки; z-условная
длина распределения сосредоточенного давления.
В нашем случае примем сечение
вспомогательных балок из І 16. Тогда в соответствии с рис.16, б будем иметь ![]()
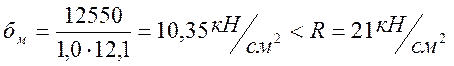
Следовательно местная прочность стенки составной балки обеспечена, в дополнительных ребрах нет необходимости.
Критические
местные напряжения определим по (1,п.6.5), так как отношение 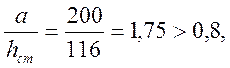 то необходимо оценить отношение
то необходимо оценить отношение 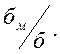
а
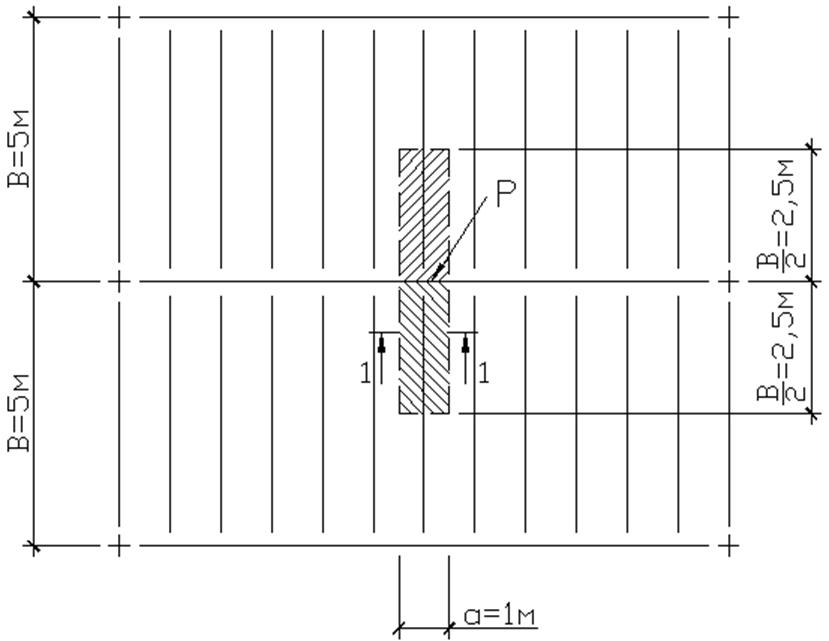
б
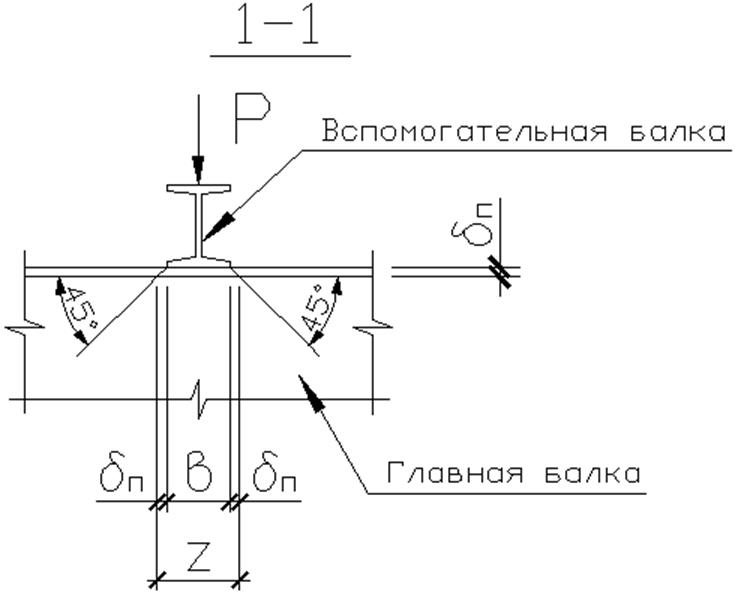
Рис. 16
Для первого
отсека в уменьшенном сечении с ![]() имеем
имеем
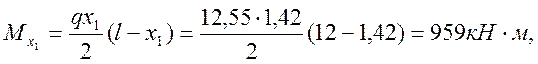 напряжение в верхних волокнах стенки
напряжение в верхних волокнах стенки 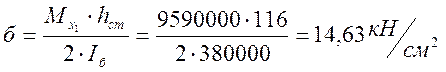 , а отношение
, а отношение 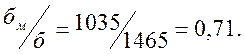
Для второго
отсека в неизмененном сечении с ![]() имеем
имеем
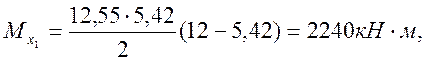
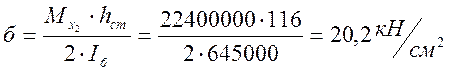
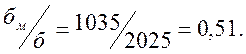
Так как в первом отсеке 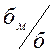 больше предельных значений, указанных в
(1, 29) при
больше предельных значений, указанных в
(1, 29) при 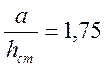 и
и ![]() (см.
выше), то в нем критические местные напряжения определяются по формуле
(см.
выше), то в нем критические местные напряжения определяются по формуле 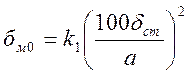 , где
, где ![]() по
(1,28) и составят
по
(1,28) и составят 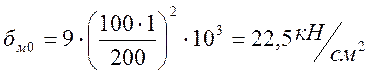 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.