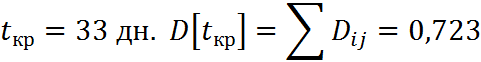
Строительство и архитектура \ Организация строительного производства

Определение продолжительности критического пути секторным способом и табличным способом, страница 2

Среднеквадратичное отклонение: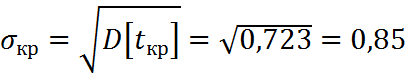

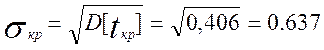
Вычисляем вероятность выполнения работ за 30 дней:

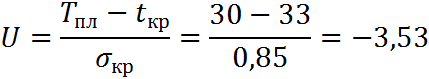
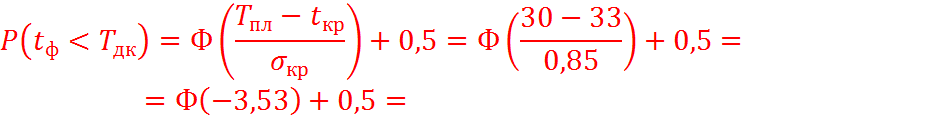
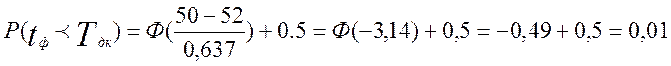
Ф(u) – функция Лапласа.

Вероятность выполнения работ за 36 дней:

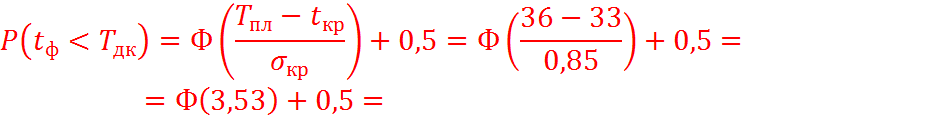
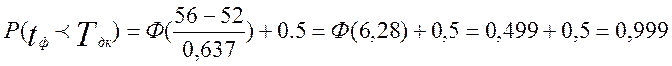
Определим время, за которое комплекс работ будет выполнен с вероятностью не меньшей P=0,7:

Ф(u)=Р – 0,5 = 0,7 – 0,5 = 0,2                         u = 0,53

Тогда

Тпл = tкр – кр*u = 52+0,637*0,53=52,3 д.

Для P=0,36:

Ф(u)=0,36- 0,5 = -0,14                                      u = -0,36

Тпл = 52+0,637*(-0,36) = 51,8 д.

Задача № 3.

Рассмотрим матрицу выполнения работ на трех частных потоках и четырех захватках. Вычислим оптимальные очередности освоения захваток несколькими потоками. Применим алгоритм направленного перебора.

А

В

С

1

2

6

4

2

2

4

1

3

7

3

2

4

1

3

3

           Т=2 +9+10=21

Рассмотрим фиктивные матрицы:

А

В

С

А

В

С

А

В

С

ˇ

А

В

С

1

2

6

4

2

2

4

1

3

7

3

2

4

1

3

3

1

3

3

3

1

3

3

3

1

3

3

3

2

6

6

4

7

3

3

2

2

6

6

4

2

6

6

4

7

3

3

2

2

4

4

1

7

3

3

2

2

4

4

1

2

4

4

1

     Т1= 2 + 7 + 10=19            Т2= 2 + 9 + 10=21        Т3= 7  +  7 + 10=24        Т4= 1 +  7 + 10=18

ˇ

А

В

С

А

В

С

А

В

С

4

1

3

3

4

1

3

3

4

1

3

3

1

2

6

4

2

2

4

1

3

7

3

2

7

3

3

2

2

6

6

4

2

6

6

4

2

4

4

1

7

3

3

2

2

4

4

1

    Т41= 1 + 7 + 10=18           Т42= 1 + 9 + 10=20       Т43= 5  +  7 + 10=22        

Переходим к реальным матрицам:

А

В

С

ˇ

А

В

С

4

1

3

3

4

1

3

3

1

2

6

4

1

2

6

4

2

2

4

1

3

7

3

2

3

7

3

2

2

2

4

1

Т4123= 1 + 8 + 10=19       Т4132= 1 + 7 + 10=18       

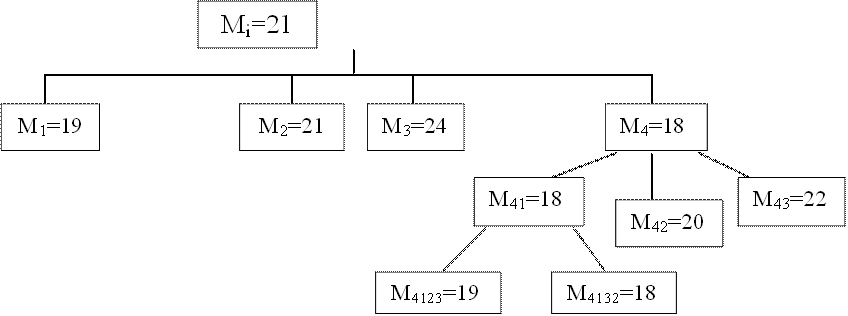Мi=21,М1=19 ,М2=21 ,М3=24 ,М4=18 ,М41=18 ,М42=20 ,М43=22 ,М4123=19 ,М4132=18
 


Таким образом, в данном случае выявлена в качестве оптимальной очередность освоения фронтов 4132, обеспечивающее минимальную продолжительность потока, равную 18 единицам времени, вместо 21.

В нижней строке фиктивных (условных) матриц показаны суммы условных периодов развертывания видов работ и продолжительности последнего вида, а в нижней строке реальных (конечных) матриц показаны суммы реальных периодов развертывания видов работ и продолжительность последнего вида, то есть Т.


Задача № 4.

Рассмотрим матрицу выполнения работ на двух частных потоках и четырех захватках. Вычислим оптимальные очередности освоения захваток несколькими потоками.

А

В

1

4

7

2

6

2

3

2

5

4

3

8

           Т=4 +22=26

А

В

3

2

5

4

3

8

1

4

7

2

6

2

           Т=2 +22=24

Таким образом, в данном случае выявлена в качестве оптимальной очередность освоения фронтов 3412, обеспечивающее минимальную продолжительность потока, равную 24 единицам времени, вместо 26.

Скачать файл