Определение продолжительности критического пути секторным способом и табличным способом

Задача № 1.

Определить продолжительность критического пути t_кр, представленного на рисунке 1 секторным способом.

Представленная на рисунке модель одноцелевая. Представляет из себя ориентированный сетевой график, включающий в себя 8 событий.

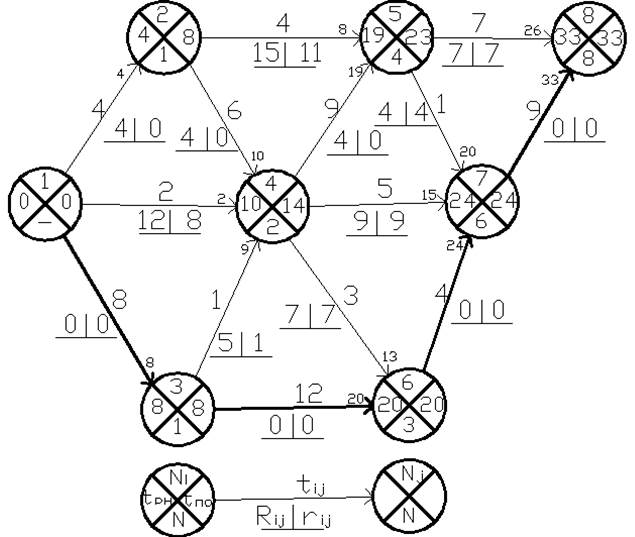
Рисунок 1 – Ориентированный сетевой график

N_i – номер исходного события;

N_j – номер завершающего события;

N – номер предшествующего события, через который проходит максимальный путь;

t_ij – продолжительность работы;

t^пн – позднее начало;

t^рн – ранее начало (max); 

t^ро – ранее окончание; 

t^по – позднее окончание (min);

R_ij – полный резерв времени;

r_ij – частный резерв времени (ранее начало последующей работы минус ранее окончание данной работы);

Таким образом, решая задачу секторным способом, получаем продолжительность критического пути t_кр= 33 дня.

Критический путь проходит через следующие события:1 – 3 – 6– 7 – 8.

Задача № 2.

Определить продолжительность критического пути t_кр, представленного на рисунке 2 табличным способом.

Исходные данные:

а_ij – оптимистическая оценка работы;

b_ij – пессимистическая оценка работы.

Определить:

1) Вероятность выполнения комплекса работ за

а) Т_пл=30 дн.

б) Т_пл=36 дн.

2) Время, за которое комплекс работ будет выполнен с вероятностью Р=0,70 и Р=0,36.

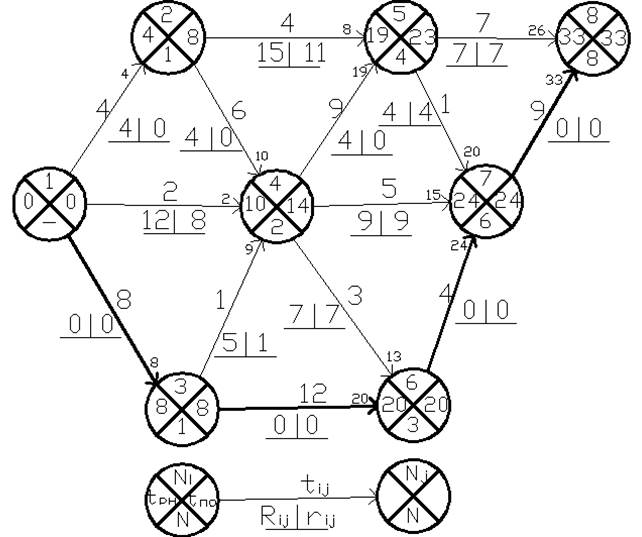
Рисунок 2 – Ориентированный сетевой график

Математическое ожидание t_ij вычисляется по формуле:

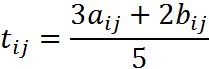
Дисперсия:

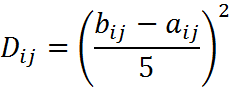
Таблица 1

Исходные параметры			Расчетные параметры
(i , j)	аij	bij	tij	Dij
1-2	3,64	4,36	4	0,021
1-3	7,27	8,73	8	0,085
1-4	1,82	2,18	2	0,005
2-4	5,45	6,55	6	0,048
2-5	3,64	4,36	4	0,021
3-4	0,91	1,09	1	0,001
3-6	10,9	13,1	12	0,194
4-5	8,18	9,82	9	0,108
4-6	2,73	3,27	3	0,012
4-7	4,55	5,45	5	0,032
5-7	0,91	1,09	1	0,001
5-8	6,36	7,64	7	0,066
6-7	3,64	4,36	4	0,021
7-8	8,18	9,82	9	0,108

Таблица 2

Шифр работ, i-j	Продолжи-тельность	Ранние сроки		Поздние сроки		Резервы времени		Работы, лежащие на критическом пути
1	2	3	4	5	6	7	8	9
1-2	4	0	4	4	8	4	0
1-3	8	0	8	0	8	0	0	на критическом пути
1-4	2	0	2	12	14	12	8
2-4	6	4	10	8	14	4	0
2-5	4	4	8	19	23	15	11
3-4	1	8	9	13	14	5	1
3-6	12	8	20	8	20	0	0	на критическом пути
4-5	9	10	19	14	23	4	0
4-6	3	10	13	17	20	7	7
4-7	5	10	15	19	24	9	9
5-7	1	19	20	23	24	4	4
5-8	7	19	26	26	33	7	7
6-7	4	20	24	20	24	0	0	на критическом пути
7-8	9	24	33	24	33	0	0	на критическом пути

Таким образом, решая задачу табличным способом, получаем продолжительность критического пути t_кр= 33 дня.

Критический путь проходит через следующие события:

1 – 3 – 6 – 7 – 8.

Продолжительность критического пути вычисляем по средним оценкам продолжительности работ:tкр=33 дня (см. табл. 2), по оптимистическим оценкам t_кр=30,03 дн., по пессимистическим t_кр=35,97 дн.

Таким образом, комплекс работ может быть выполнен с определенной вероятностью в любой срок интервала [30,03 – 35,97].

Так как 4 работы лежат на критическом пути, то его длина подчиняется нормальному закону распределения.

Параметры критического пути: