Исследуйте зависимость между стоимостью продукции (результативный признак) и стоимостью основных производственных фондов (факторный признак). На основании исходных данных:
1. постойте поле корреляции; составьте корреляционную таблицу; нанесите эмпирическую линию регрессии на поле корреляции и сделайте предположение о возможной форме связи.
2. В целях синтезирования моделей зависимости задайте вид и вычислите параметры уравнения связи, нанесите полученную линию регрессии на график;
3. Сделайте выводы по п.2;
4. Используя полученную модель, сделайте прогноз стоимости продукции для предприятия со стоимостью основных фондов 14 млрд. руб.
Решение.
1. Поле корреляции имеет вид:
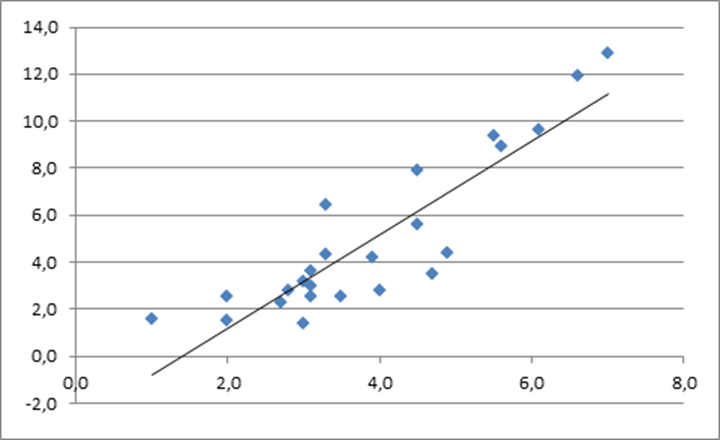
По оси абсцисс расположены значения стоимости ОПФ, по оси ординат – стоимость выпуска продукции. Предположительно связь результативного и факторного признака линейная, что отражено линией тренда на точечной диаграмме.
Построим ряд распределения предприятий по объему выпуска, разделив исходный ряд на шесть интервалов. Для этого необходимо вычислить длину интервала I:
![]() , где xmax –
максимальное значение признака,
, где xmax –
максимальное значение признака,
xmin – минимальное значение признака,
n – число интервалов.
xmax
= 12,9, xmin = 1,4, n = 6, отсюда I
= ![]() = 1,92
= 1,92
Следовательно, ряд распределения предприятий по объему выпуска примет следующий вид:
|
Интервал |
Частота |
|
1,6 – 3,5 |
12 |
|
3,5 – 5,4 |
4 |
|
5,4 – 7,4 |
2 |
|
7,4 – 9,3 |
2 |
|
9,3 – 11,2 |
2 |
|
11,2 – 13,1 |
2 |
Частоты интервалов соответствуют количеству предприятий в каждой группе.
I группа.
|
№ предприятия |
y |
x |
|
1 |
2,5 |
3,5 |
|
2 |
2,8 |
4,0 |
|
3 |
1,6 |
1,0 |
|
7 |
2,8 |
2,8 |
|
10 |
2,5 |
2,0 |
|
11 |
3,5 |
4,7 |
|
12 |
2,3 |
2,7 |
|
13 |
3,2 |
3,0 |
|
15 |
1,5 |
2,0 |
|
19 |
1,4 |
3,0 |
|
20 |
3,0 |
3,1 |
|
21 |
2,5 |
3,1 |
|
ср. знач. |
2,47 |
2,91 |
II группа.
|
№ предприятия |
y |
x |
|
6 |
4,4 |
4,9 |
|
16 |
4,2 |
3,9 |
|
18 |
4,3 |
3,3 |
|
23 |
3,6 |
3,1 |
|
ср. знач. |
4,1 |
3,8 |
III группа.
|
№ предприятия |
y |
x |
|
5 |
5,6 |
4,5 |
|
17 |
6,4 |
3,3 |
|
ср. знач. |
6 |
3,9 |
IV группа.
|
№ предприятия |
y |
x |
|
22 |
7,9 |
4,5 |
|
24 |
8,9 |
5,6 |
|
ср. знач. |
8,4 |
5,1 |
V группа.
|
№ предприятия |
y |
x |
|
8 |
9,4 |
5,5 |
|
14 |
9,6 |
6,1 |
|
ср. знач. |
9,5 |
5,8 |
VI группа.
|
№ предприятия |
y |
x |
|
4 |
12,9 |
7,0 |
|
9 |
11,9 |
6,6 |
|
ср. знач. |
12,4 |
6,8 |
Вывод: проанализировав средние значения объема выпуска и стоимости основных производственных фондов по группам, можно сказать, что при увеличении стоимости ОПФ наблюдается увеличение объема выпуска. Это свидетельствует о наличии связи между факторным и результативным признаком.
2. Вычислим параметры уравнения связи результативного и факторного признака, добавим линию тренда на график. Характеристикой качества уравнения является коэффициент детерминации R2.
Интервал
значений: ![]() Чем ближе
Чем ближе ![]() к 1, тем лучше качество
построенного уравнения регрессии.
к 1, тем лучше качество
построенного уравнения регрессии.
a) Линейный тренд
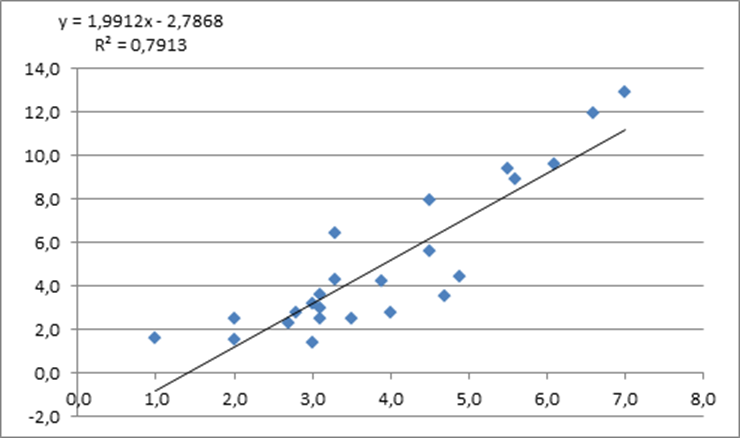
b) Логарифмический тренд
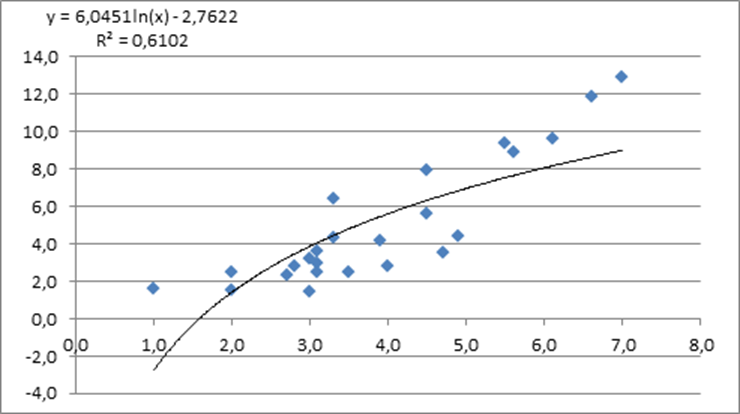
c) Полиномиальный тренд, степень полинома 2.
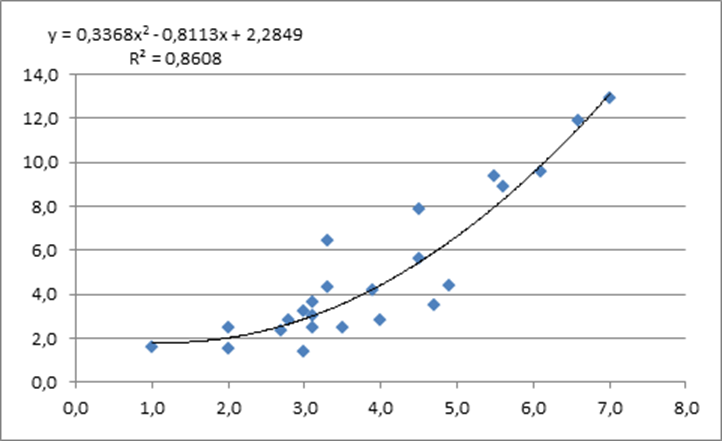
Экспоненциальный тренд
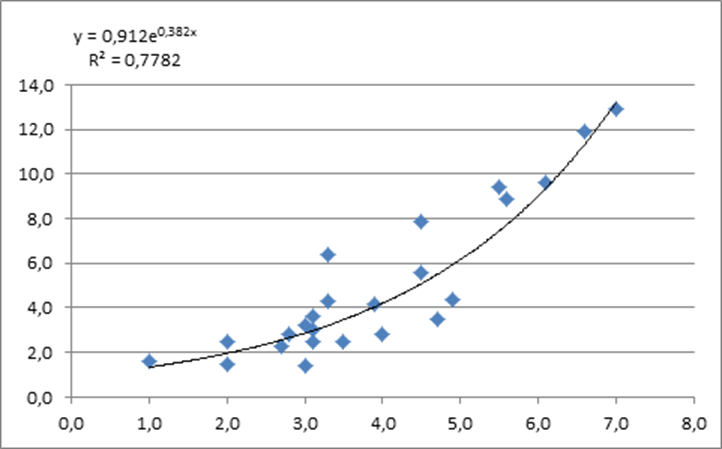
Вывод: в результате изучения данных получаем, что зависимость объема выпуска продукции от стоимости ОПФ можно записать с помощью полиномиального тренда второй степени. Этот вывод основан на анализе значений коэффициентов детерминации полученных уравнений (R2 полиномиального тренда наибольший, равен 0,86).
3. Прогноз стоимости продукции предприятия для предприятия со стоимостью ОПФ 14 млрд.руб.:
![]()
![]()
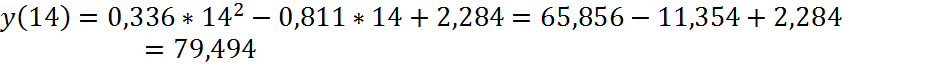
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.