Составление математического описания гомогенных реакторов идеального смешения и идеального вытеснения с заданным механизмом сложной химической реакции, страница 2

Типовые модели гидродинамики построены на основе тех или иных допущений относительно характера движения элементов потока в аппарате и представляют собой некоторую идеализацию реального процесса. Модель идеального вытеснения предполагает, что все элементы потока движутся с одинаковой скоростью и имеют одинаковое время пребывания.  МО движения такого потока, полученное из материального баланса по индикатору для элементарного участка аппарата длиной dx  имеет следующий вид.

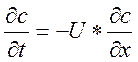                                                            (5)

Где с – концентрация индикатора, t– текущее время, x – координата по длине реактора,U– линейная скорость потока.

Модель идеального смешения предполагает, что поток, поступающий в аппарат, мгновенно перемешивается, вследствие чего концентрация индикатора во всём объёме аппарата одинакова и равна концентрации на выходе. МО движения такого потока, полученное из материального баланса по индикатору для аппарата в целом имеет следующий вид.

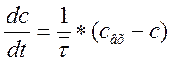                                                         (6)

Где  - среднее время пребывания потока в аппарате, определяемое как отношение объёма аппарата к объёмной скорости потока; с_вх – концентрация индикатора на входе в аппарат.

Следует отметить, что модели гидродинамики (5) и (6) являются динамическими, т.к. описывают нестационарный процесс изменения концентрации индикатора при нанесении возмущения.

1.3. Математическое описание гомогенного реактора.

МО реактора в целом строится на основе агрегирования (синтеза) МО подсистем.  Для разработки МО реактора идеального вытеснения (РИВ) необходимо на основе модели гидродинамики (5) составить материальный баланс по всем компонентам, участвующим в химической реакции с учётом кинетических закономерностей (3).

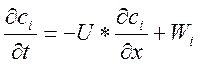     i= 1,2..n                                           (7)

В стационарных условиях работы реактора 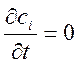. С учётом того, что dx/U = τ (τ- текущее время пребывания в реакторе), систему уравнений (7) можно представить в виде:

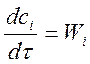                      i= 1,2..n(8)

Если заменить правые части системы выражением (3), то МО РИВ в стационарных условиях в матричной форме примет вид

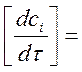[]            i= 1,2..n                                      (9)

Начальными условиями для решения системы (9) будут концентрации всех компонентов на входе в реактор (С_вхi):

τ = 0        С_i=С_вхii= 1,2..n              (10) 

Если принять, что в РИВ протекает реакция, рассмотренная в примере, то МО РИВ:

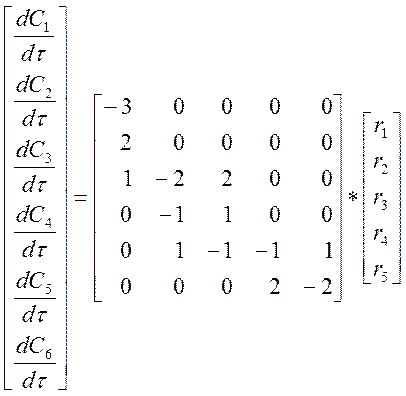                             (11)

С граничными условиями (10).

          Результатом решения системы уравнений МО РИВ являются профили концентраций по времени пребывания (по длине реактора).

Для разработки МО реактора идеального смешения (РИС) необходимо также составить материальный баланс по всем компонентам, участвующим в химической реакции с учётом кинетических закономерностей (3), но на основе модели гидродинамики (6)

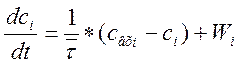             i= 1,2..n                           (12)

Если заменить  в правой части системы (12) выражением (3), то МО РИС в нестационарных условиях в матричной форме примет вид

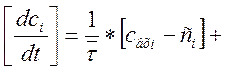[]            i= 1,2..n                       (13)

Начальными условиями для решения системы (13) будут концентрации всех компонентов  в реакторе в начальный момент времени (С_0i):

τ = 0        С_i=С_0ii= 1,2..n                                        (14) 

В частном случае, если моделируется процесс пуска реактора,  С_0i=0.

Если принять, что в РИС протекает реакция, рассмотренная в примере, то МО РИС:

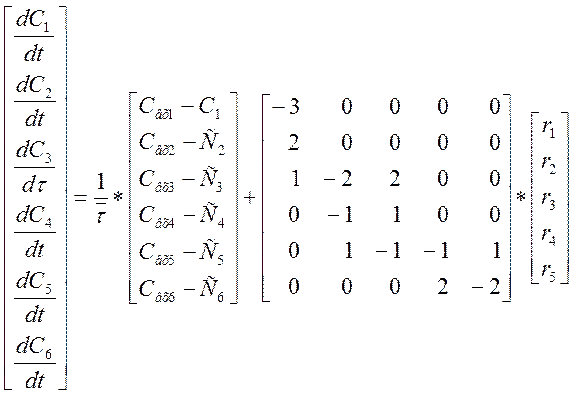                        (15)

с начальными условиями   (14).

Решением МО РИС является изменение концентраций компонентов в реакторе с течением времени. Моделирование процесса пуска реактора позволяет определить время выхода реактора на стационарный режим (время переходного процесса) и концентрации на выходе из реактора в стационарном режиме.

2. Реализация математического описания в Simulink.

          Решение  поставленной задачи в Simulink осуществляется в соответствии с технологией, рассмотренной в предыдущих лабораторных работах. За основу может быть принята  S-модель решения системы обыкновенных дифференциальных уравнений из Лабораторной работы №1. Элементы вектора  можно вычислить с помощью блоков Fcn (например, для решения систем (11) и (15) таких блоков будет 5), а объединить их в вектор - с помощью мультиплексора. 

          После настройки параметров блоков и запуска модели на выполнение, следует получить результаты в графическом виде и в виде таблицы. Для определения времени завершения переходного процесса в РИС следует увеличивать модельное время до достижения условия постоянства концентраций во времени. По результатам моделирования, сравнивая концентрации продукта реакции на выходе из РИВ и РИС в стационарных условиях, можно выбрать эффективный реактор для проведения рассматриваемой реакции.

          Исходные данные для моделирования: механизм химической реакции, константы скорости стадий и концентрации на входе в реактор – в индивидуальном задании. Время пребывания в реакторах РИВ и РИС  принять равным 10 мин.