Составление математического описания гомогенных реакторов идеального смешения и идеального вытеснения с заданным механизмом сложной химической реакции

Лабораторная работа  №3

Цель работы: На основе принципов системного анализа составить математическое описание гомогенных реакторов идеального смешения и идеального вытеснения с заданным механизмом сложной химической реакции, выполнить программную реализацию в виде S – моделей и по результатам моделирования рекомендовать наиболее эффективный реактор.

1. Системный анализ гомогенного химического реактора.

Цель СА в данном случае - разработка математической модели реактора. Реактор осуществляет преобразование исходных реагентов на входе в продукты химической реакции на выходе.  В гомогенном реакторе все компоненты находятся в одной фазе (жидкость, газ). Реактор можно представить как систему, элементами которой являются отдельные физико-химические процессы, т.е. как физико-химическую систему (ФХС). Системный анализ, как метод исследования сложных систем, предполагает последовательный переход от общего к частному, исследование частного и объединение в целое. Т.о. СА представляет собой сочетание двух процедур: декомпозиции и агрегирования.  Выполним декомпозицию (анализ) ФХС:

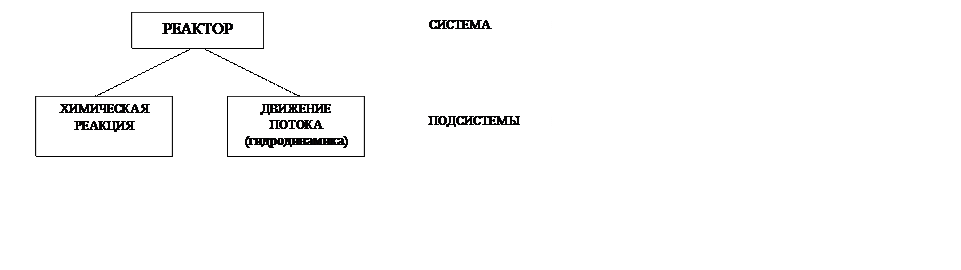
Каждую из подсистем рассмотрим как систему более низкого уровня по отношению к системе «РЕАКТОР».

1.1. Математическое описание подсистемы «химическая реакция»

Подсистему «химическая реакция» можно рассмотреть как систему, в которой происходят взаимодействия между компонентами на уровне молекул. Элементы системы – компоненты, участвующие в реакции, а связь между компонентами определяется маршрутом химической реакции. Присутствуют все признаки системы (покажите самостоятельно!).  Количественной характеристикой элементов системы  или параметрами системы являются концентрации компонентов, а параметрами, характеризующими связи – константы скорости реакций. Изменение концентраций реагентов в ходе реакции определяется кинетикой химической реакции.  Если механизм химической реакции известен, то математическое описание (МО) кинетики можно представить в матричной форме. Процедура составления МО в матричной форме достаточно хорошо формализована и состоит в следующем.

1. Составляются уравнения скоростей  отдельных стадий химической реакции:

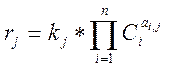                                  j = 1,..m                                                        (1)

где       r_j – скорость j –ой стадии (число стадий m),  k_j - константа скорости j –ой     стадии, C_i – концентрация i –го исходного реагента,  – стехиометрический коэффициент i –го компонента в j –ой стадии, n– число реагентов.

2. Составляются уравнения скоростей реакций по компонентам:

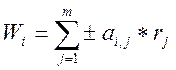                                               i=1,..n(2)

где  W_i – скорость реакции по i-му компоненту.

Систему (2) с учётом (1) можно представить в матричной форме:

                                     [W_i] = []                                                                  (3)

где  [W_i]- вектор из n элементов, - вектор из m элементов, [] – матрица стехиометрических коэффициентов размерностью nm. Элемент матрицы, стоящий на пересечении i – ой строки и j – го столбца – это стехиометрический коэффициент  i – го компонента в j – ой стадии взятый со знаком «-» для исходных реагентов и со знаком «+» для продуктов реакции.

Пример.  Задан механизм сложной химической реакции

Число реагентов n = 6, число стадий m = 5 (по числу констант).

Скорости стадий в соответствии с (1): 

                                             

                                                       

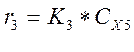
Скорости реакций по компонентам в соответствии с (3):

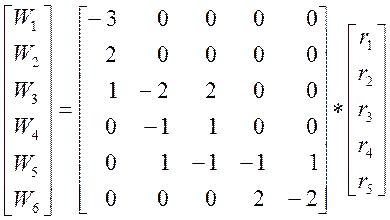                                                                       (4)

Система (4) представляет собой математическое описание кинетики химической реакции заданного механизма.

1.2. Математическое описание подсистемы «движение потока».

Подсистему «движение потока» или «гидродинамика»можно рассмотреть как систему, в которой происходит движение частиц потока жидкости или газа, причем частицы имеют различную скорость и  траекторию  движения, изменяющиеся случайным образом.   Частицы потока – это элементы системы. Здесь также присутствуют все признаки системы (покажите самостоятельно!).  Разработка математического описания этой системы встречает на своем пути определённые трудности. Невозможно  описать движение каждой частицы потока, при условии, что таких частиц бесконечное множество и траектория их движения может изменяться случайным образом, поэтому в теории математического моделирования гидродинамики используется  следующий подход.

Каждой частице потока ставится в соответствие время её пребывания в аппарате. Величина времени пребывания рассматривается как случайная, а доля частиц с заданным временем пребывания в общей массе частиц представляет собой вероятность случайной величины.  Для получения эмпирической плотности распределения или эмпирической функции распределения времени пребывания проводят специальный эксперимент. В поток на входе в аппарат вводят некоторый индикатор в виде импульсного или ступенчатого возмущения, т.е. помечают поступающие в аппарат частицы потока, а на выходе из аппарата снимают кривую отклика в виде зависимости концентрации индикатора от времени, т.е. фиксируют выходящие из аппарата частицы. Кстати, S-модель подобного эксперимента, проведённого на ёмкости с мешалкой, рассматривалась в последней задаче лаб. раб.№1. Преобразованная определённым образом кривая отклика на импульсное возмущение представляет собой эмпирическую плотность распределения, а кривая отклика на ступенчатое возмущение – эмпирическую функцию распределения элементов потока по времени пребывания в аппарате. По виду функции или плотности распределения выбирают одну из типовых моделей гидродинамики и при необходимости определяют её параметры.