Ŷ = 25,54 - 7248,22 * X
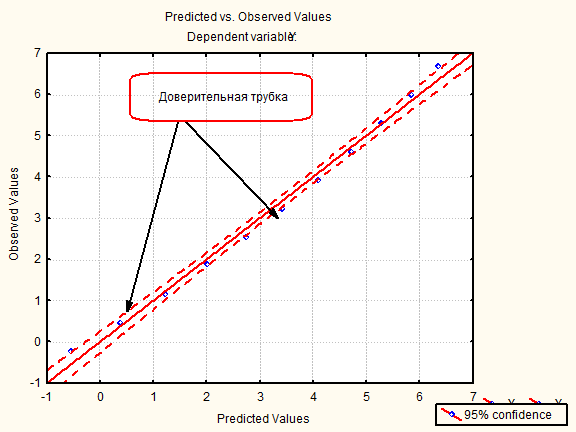
Насколько точно описывает полученная зависимость результаты эксперимента можно судить по величине коэффициента корреляции (R) и коэффициента детерминации (R?) - их значения достаточно близки к 1. Визуально судить о точности можно по графику соответствия наблюдаемых (Observed) Y и рассчитанных по регрессии (Predicted) Ŷ значений отклика. Для вывода графика необходимо щелкнуть по кнопке Multiple Regression… на панели анализа окна пакета, перейти на вкладку Residuals/assumptions/prediction и щелкнуть по клавише Perform residual analysis (Анализ остатков). В окне анализа остатков Residual Analysis выбрать вкладку Scatterplots и щелкнуть по клавише Predicted vs. Observed. Если все точки находятся внутри доверительной трубки, найденная регрессия достаточно точно отражает экспериментальные данные (с вероятностью 95%). Если точка лежит точно на прямой, это означает, что при одном и том же значении фактора экспериментальное значение отклика совпадает с расчётным.
Теперь можно перейти к параметрам уравнения Аррениуса:
К0 = e25,54 = 1,24*1011,
E= 7248,22 * 8,31 = 60232,7082
Для расчета К0 иEпо вашим данным следует в таблицу данных добавить две переменных К0 и Е, ввести для них расчетные формулы (2.5) и (2.6) с найденными коэффициентами и выполнить расчёт по этим формулам.
Уравнение Аррениуса с найденными параметрами для рассматриваемого примера запишем в виде
K = 1,24*1011 * e-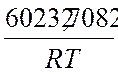
Математический анонс.
При обработке экспериментальных данных довольно часто предполагается нелинейная зависимость между откликом Y и несколькими (или одним) факторами X1, X2,…Xn, причём вид функциональной зависимостиY(X1, X2,…Xn) может быть известен и по экспериментальным данным требуется оценить неизвестные параметры зависимости.
Например, в рассмотренной выше задаче известно, что зависимость константы скорости реакции от температуры имеет вид экспоненты (2.3) и по экспериментальным данным требуется оценить К0 и E.
Для решения этой задачи используются численные методы оптимизации, относящиеся к классу методов нелинейного программирования: квазиньютоновский метод, симплекс, метод Розенброка, Хука-Дживса, могут использоваться и комбинации этих методов. В качестве минимизируемой функции наиболее часто используется, как и в линейной регрессии, сумма квадратов остатков.
Поиск нелинейной зависимости в модуле.
Решим ту же задачу, что решали в модулеЛинейная множественная регрессия: найдем оценки параметров К0 и Eв уравнении Аррениуса (2.3), но в этом случае не будем приводить зависимость к линейному виду. Данные возьмём из файла Arr№группы_№компьютера. Откликом в этой задаче является константа скорости реакции К, фактором – температура tв 0С.
1. Вызов стартовой панели модуля и задание вида нелинейной функции. Прежде всего, в окнеSTATISTICA должна быть открыта таблица с обрабатываемыми данными. Если таблицы нет или открыта не та таблица, следует открыть соответствующий файл данных (см. html - документ Операции с таблицами).
· Для вызова стартовой панели модуля в меню команд щелкнуть Statistics, выбрать AdvancedLinear/NonlinearModelsи в подменю щелкнуть NonlinearEstimation.
· В окне стартовой панели модуля выбрать User-specifiedregression, customlossfunction(регрессия, специфицированная пользователем и выбор минимизируемой функции для поиска оценок параметров) и щёлкнуть ОК.В открывшемся окне щелкнуть кнопку Functiontobeestimated & lossfunction, в полеEstimatedfunction(оцениваемая функция) следует ввести функцию, в нашей задаче следует ввести
K=KR0*exp(-ER/(8.31*(t+273)))
Введены новые обозначения оцениваемых параметров KR0 и ER, т.к. K0 и E в таблице уже существуют.
2. Выбор минимизируемой функции и численного метода поиска оценок параметров.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.