




Определение. Несобственный интеграл называется условно-сходящимся, если он сходится, но не является абсолютно-сходящимся.
Пример. 1. 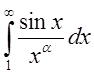 .
.
При
![]() интеграл сходится абсолютно, т.к.
интеграл сходится абсолютно, т.к. 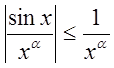 , а
, а 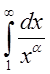 сходится.
сходится.
При
![]() абсолютной сходимости нет:
абсолютной сходимости нет:
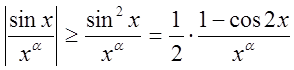
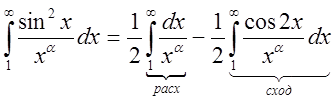 , где
, где 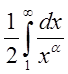 расходится.
расходится.
2.
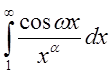 .
.
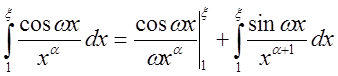 , где
, где 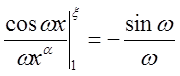 при
при ![]() , и
, и 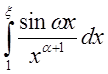 имеет
конечный предел, т.е. он сходится.
имеет
конечный предел, т.е. он сходится. ![]()
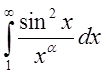 расходится
+ сходится
расходится
+ сходится ![]() расходится
расходится ![]()
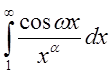 расходится при
расходится при ![]() .
.
Однако,
этот интеграл является условно-сходящимся, т.к. 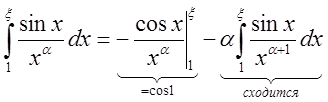 .
.
Функции нескольких переменных.
Определение. ![]() - пространство точек
- пространство точек ![]() с расстоянием
с расстоянием ![]() .
.
Свойства расстояния:
1.
![]()
2.
![]()
3.
![]()
Определение. ![]() .
.
Определение. Шар радиуса ![]() с
центром в точке
с
центром в точке ![]() :
: ![]()
Определение. Точка ![]() называется внутренней
точкой множества
называется внутренней
точкой множества ![]() , если
, если ![]() .
.
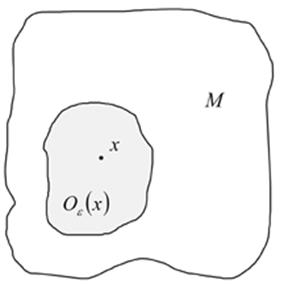
Определение.
Точка ![]() называется внешней для множества
называется внешней для множества ![]() , если
, если ![]()
![]() (т.е.
(т.е. ![]() не
пересекается с множеством
не
пересекается с множеством ![]() ).
).
Определение.
Точка ![]() называется граничной точкой множества
называется граничной точкой множества ![]() , если она не является ни внутренней, ни
внешней, т.е.
, если она не является ни внутренней, ни
внешней, т.е. ![]() включает точки, как
принадлежащие, так и не принадлежащие
включает точки, как
принадлежащие, так и не принадлежащие ![]() .
.
Примеры.
1.
![]() .
.
![]()
Тогда
внутренние точки: ![]() .
.
Внешние:
![]() и
и ![]() .
.
Граничные:
![]() и
и ![]() .
.
2.
На ![]() :
: ![]() .
.
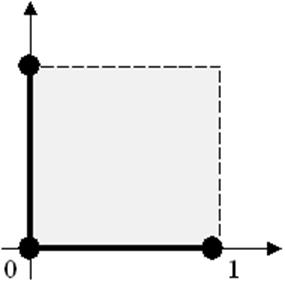
Внутренние
точки: ![]() .
.
Внешние
точки: точки, для которых либо ![]() либо
либо ![]() .
.
3.
![]() .
.
Внутренних
и внешних точек нет ![]() все точки граничные.
все точки граничные.
4.
![]() в
в ![]() .
.
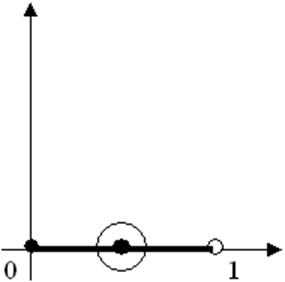
Внутренних точек нет, т.к. любая окрестность не включается в полуинтервал.
Внешние
и граничные точки: все точки, не принадлежащие ![]() .
.
Определение.
Множество ![]() называется открытым, если все его точки
являются внутренними (точки границы не входят в множество).
называется открытым, если все его точки
являются внутренними (точки границы не входят в множество).
Определение.
Множество ![]() называется замкнутым, если все граничные
точки принадлежат
называется замкнутым, если все граничные
точки принадлежат ![]() .
.
Примеры.
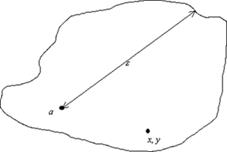 1.
1.
![]() - открытое множество.
- открытое множество.
Пусть
![]() . Тогда
. Тогда ![]() если
если ![]() .
.
В
самом деле, если ![]() , то
, то ![]() .
.
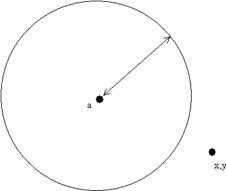
2.
![]() является замкнутым.
является замкнутым.
Если
![]() . Тогда
. Тогда ![]() - не
граничная точка, а внешняя:
- не
граничная точка, а внешняя: ![]()
![]() .
.
![]() . Действительно, если
. Действительно, если ![]() , то
, то ![]() -
является замкнутым.
-
является замкнутым.
Определение.
Множество ![]() называется ограниченным, если оно целиком
лежит в некотором шаре
называется ограниченным, если оно целиком
лежит в некотором шаре ![]() .
.
Например,
любой прямоугольник в ![]() ограничен, т.к. его можно
включить в шар с центром в начале координат.
ограничен, т.к. его можно
включить в шар с центром в начале координат.
Ограниченность
множества М означает, что ![]()
![]() (
(![]() ).
).
Полуплоскость
в ![]() - не ограниченное множество.
- не ограниченное множество.
Рассмотрим
отображение (правило, сопоставляющее любой точке из М её точку из ![]() ).
).
![]()
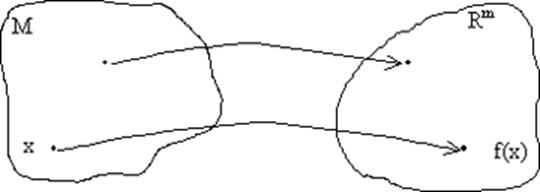
Определение.
Отображение называется непрерывным в точке ![]() , если
точка
, если
точка ![]() является внутренней для
является внутренней для ![]() и
и ![]()
![]()
![]()
![]() .
.
Определение.
Кроме того, ![]() называется пределом отображения
называется пределом отображения ![]() , если
, если ![]()
![]()
![]()
![]() .
.
Определение.
Таким образом, отображение называется непрерывным в точке ![]() , если
, если ![]() .
.
Теорема. О непрерывности сложного отображения.
Пусть
![]() непрерывно в точке
непрерывно в точке ![]() и
и
![]() непрерывна в точке
непрерывна в точке ![]() .
Тогда сложное отображение, определённое в
.
Тогда сложное отображение, определённое в ![]() ,
непрерывно в точке
,
непрерывно в точке ![]() .
.
Доказательство условно совпадает с доказательством теоремы о непрерывности сложной функции.
Определение.
Отображение ![]() называется функцией нескольких переменных.
называется функцией нескольких переменных.
Например,
![]()
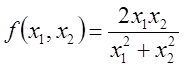
![]()
Если
функция задана в ![]() или
или ![]() , то
вместо
, то
вместо ![]() или
или ![]() , пишут
чаще
, пишут
чаще ![]() или
или ![]() .
.
Определение.
Будет писать, что 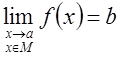 , если
, если ![]()
![]()
![]() . Такой предел
называется пределом по множеству
. Такой предел
называется пределом по множеству ![]() .
.
Пример. ![]()
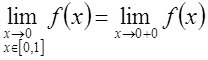 ,
, 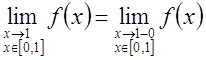
Пример.
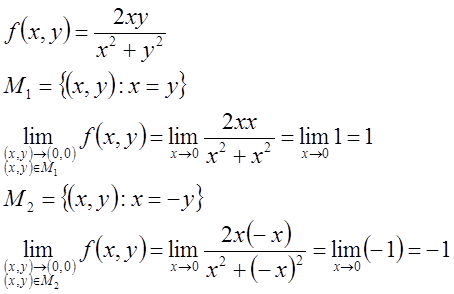
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.