Центральное растяжение и сжатие статически определимого прямого ступенчатого стержня. Статически неопределимые стержневые системы. Геометрические характеристики плоских сечений

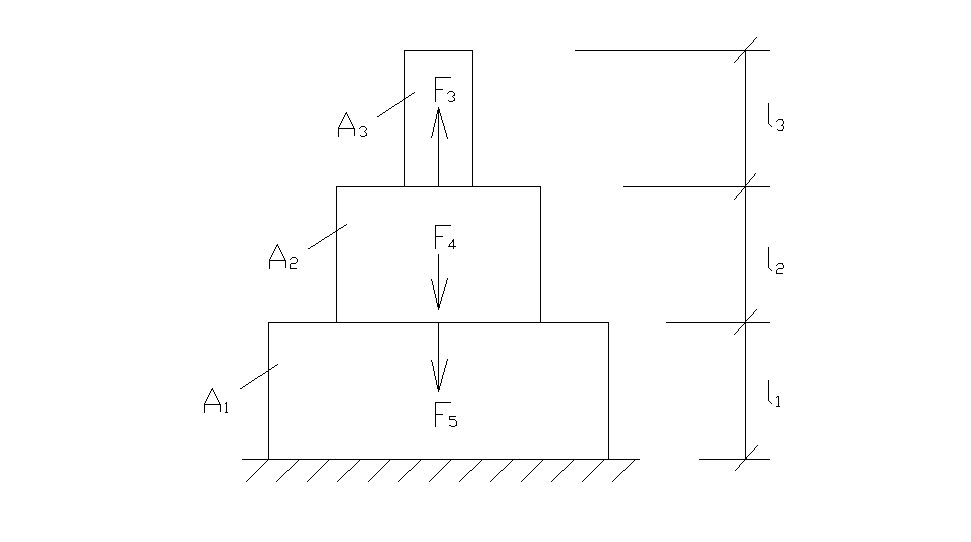
Задача 1.1.  Центральное растяжение и сжатие статически определимого прямого ступенчатого стержня

Ступенчатый стержень находится под действием продольных расчетных сил F_i, приложенных по концам или в центре соответствующего участка стержня. Материал стержня – сталь с допускаемым напряжением σ_адм = 160 МПа.

Требуется:

1.  Построить эпюры продольных сил, напряжений и перемещений;

2.  Оценить прочность стержня.

l₁ = 54 см                  А₁ = 4 см²                    F₃ = 140 кН                                                              

l₂ = 68 см                  А₂ = 8 см²                    F₄ = 100 кН                                                                                        

l₃ =  48 см                 А₃ = 12 см²                  F₅ = 80 кН                                                                                       

Решение

1.    Определим продольные усилия на участках:

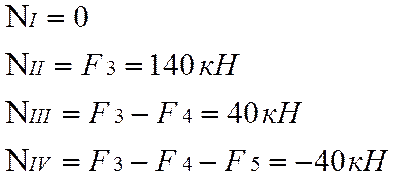
По полученным значениям построим эпюру внутренних продольных усилий N.

2.  Определим нормальные напряжения по участкам:

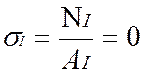
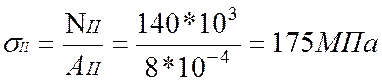
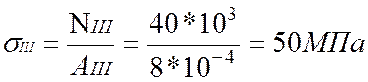
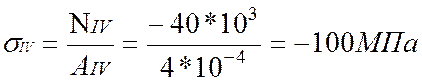
По полученным значениям построим эпюру нормальных напряжений σ.

3.  Определим перемещения характерных сечений бруса:

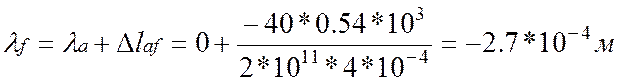
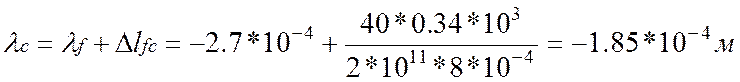
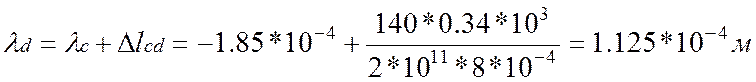
По полученным значениям построим эпюру перемещения λ.

4.  Оценим прочность стержня.

σ _max=175 МПа  >  σ_адм=160 МПа

Условия прочности не выполняются.

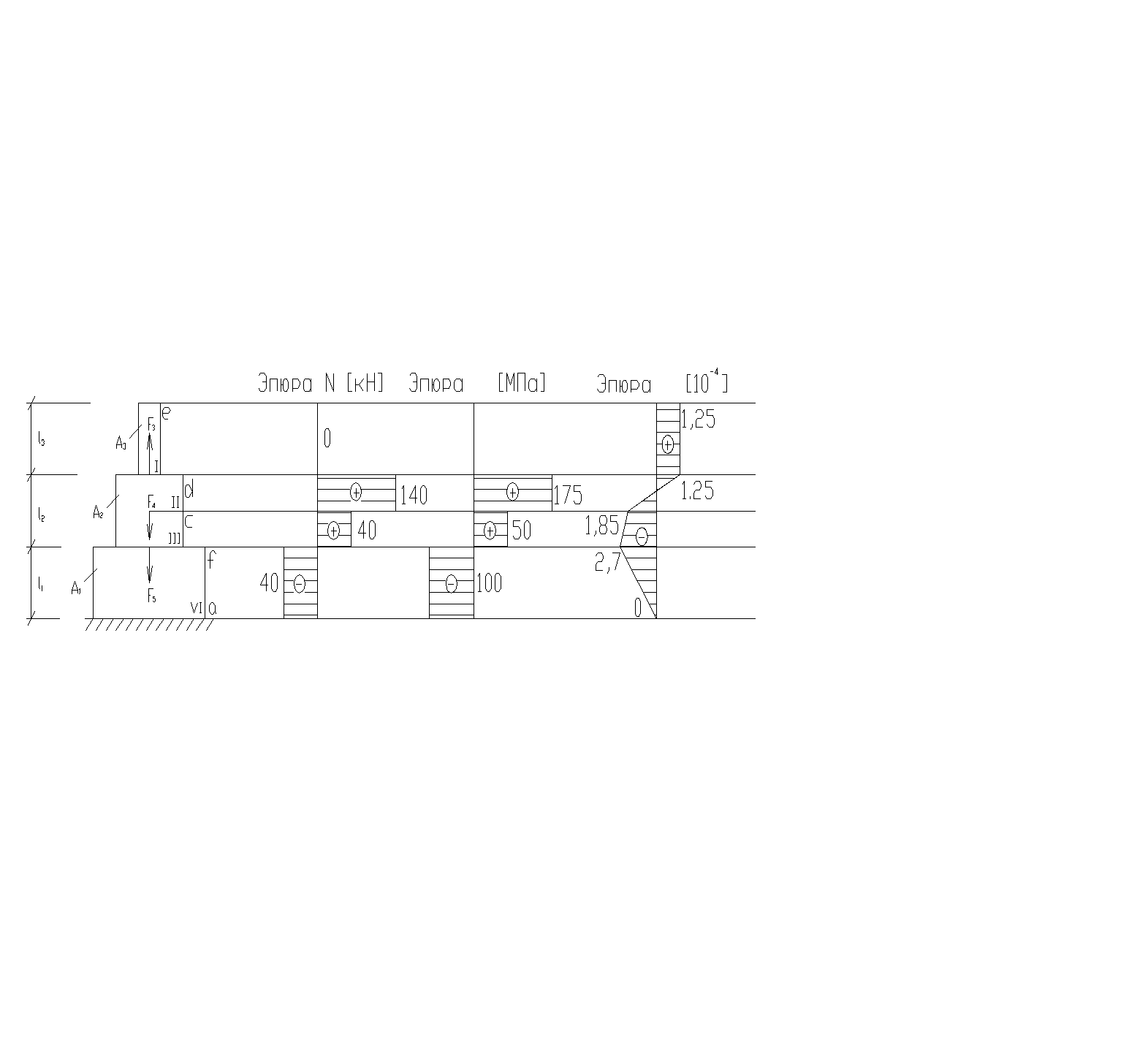
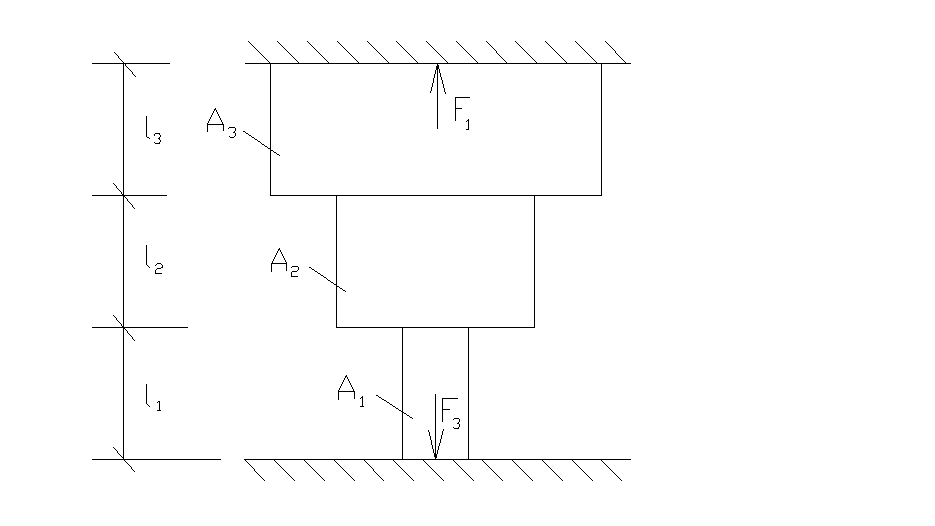
          Задача 1.2.  Центральное растяжение и сжатие статически неопределимого прямого ступенчатого стержня

Ступенчатый стержень нагружен продольными расчетными силами F_i. Материал стержня – сталь с допускаемым напряжением σ_адм = 160 МПа. Внешние силы придожены к участкам

Требуется:

1.  Построить эпюры продольных сил, напряжений и перемещений;

2.  Оценить прочность стержня.

l₁ = 54 см                  А₁ = 4 см²                    F₃ = 140 кН                                                              

l₂ = 68 см                  А₂ = 8 см²                    F₄ = 100 кН                                                                                        

l₃ =  48 см                 А₃ = 12 см²                  F₅ = 80 кН                                                                                      

Решение

1. 

 

;  

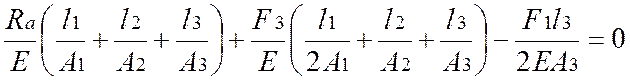
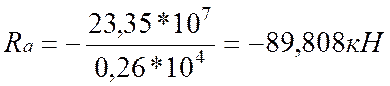
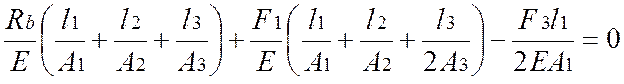
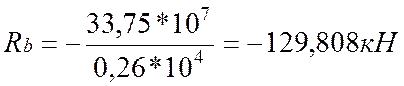
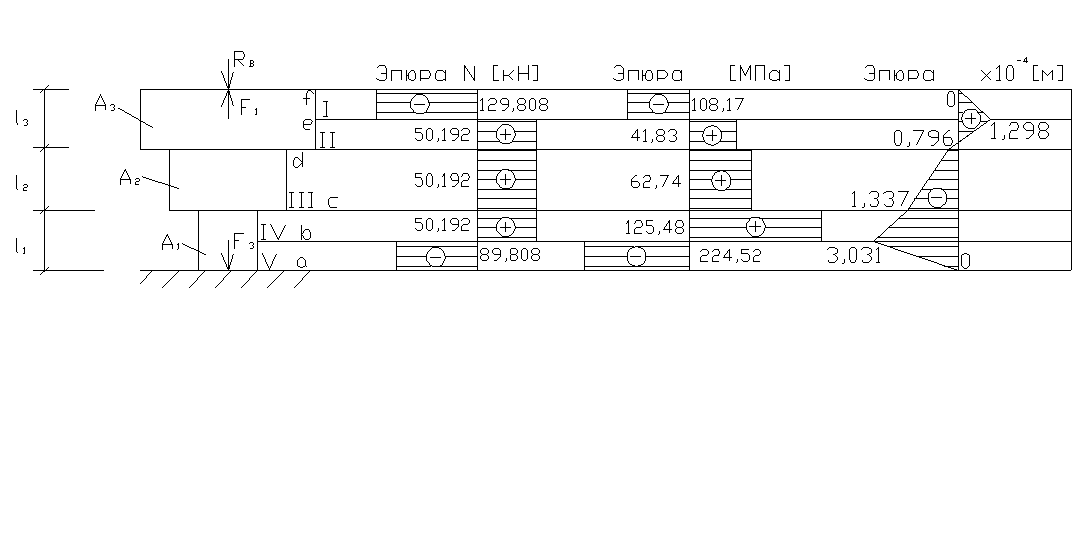
2.  Определим продольные усилия на участках:

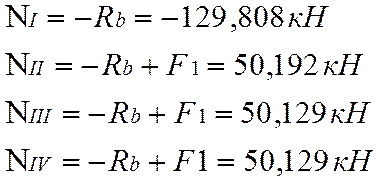
По полученным значениям построим эпюру внутренних продольных усилий N.

3. 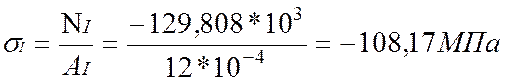 Определим нормальные напряжения по участкам:

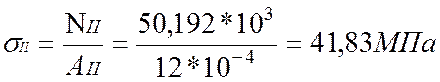
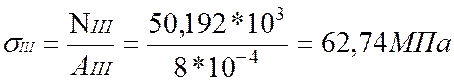
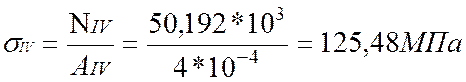
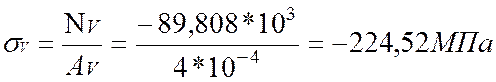
По полученным значениям построим эпюру нормальных напряжений σ.

4.  Определим перемещения характерных сечений бруса:

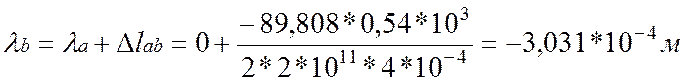
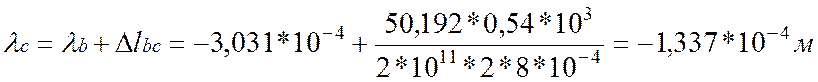
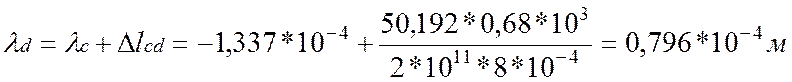
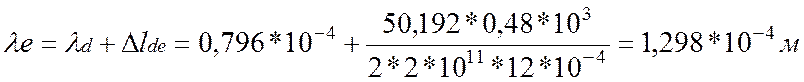
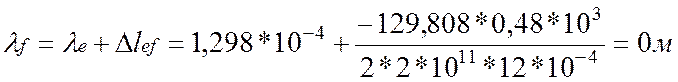
По полученным значениям построим эпюру перемещения λ.

3.  Оценим прочность стержня.

σ_max=224,52МПа  >  σ_адм=160 МПа

Условия прочности не выполняются.

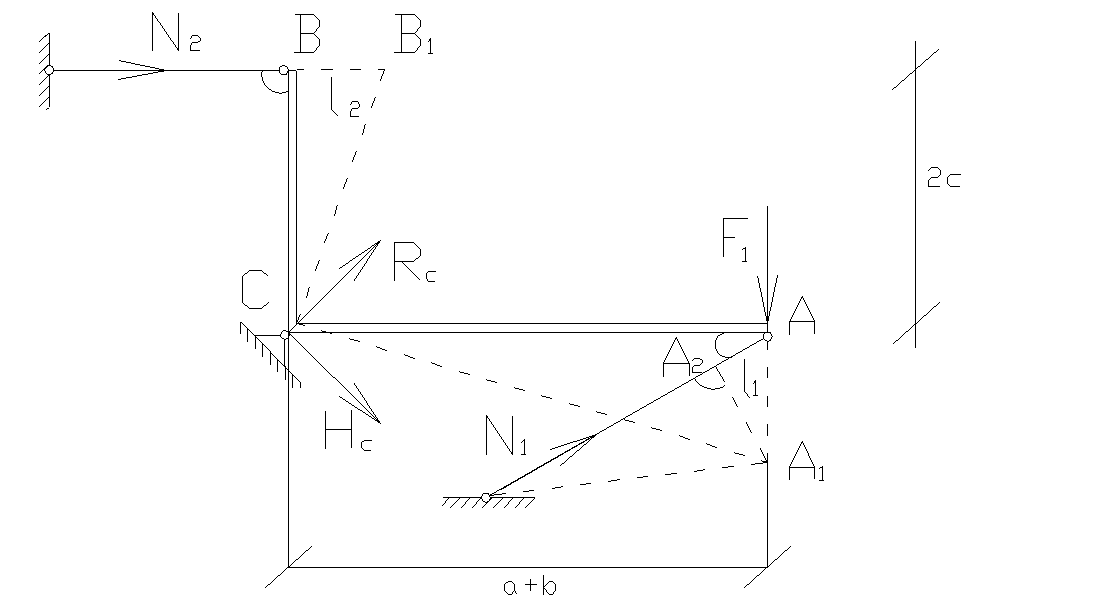
Задача 1.3.  Статически неопределимые стержневые системы.

На систему, состоящую из элемента большой жесткости и двух стальных стержней, действует расчетная нагрузка. Допускаемое напряжение стали σ_adm = 160 МПа.

Требуется:

1.  Определить напряжения в стержнях при заданных значениях нагрузки и площадях сечений стержней;

2.  Определить допускаемую нагрузку на систему.

l₁ = 1,4 м                  А₁ = 6 см²                    α₁ = 30^о                          а = 5 м

l₂ = 1,2 м                  А₂ = 7 см²                    α₂ = 90^о                          b = 2 м

F₁ = 25 кН                                                                                     c = 1,6 м       

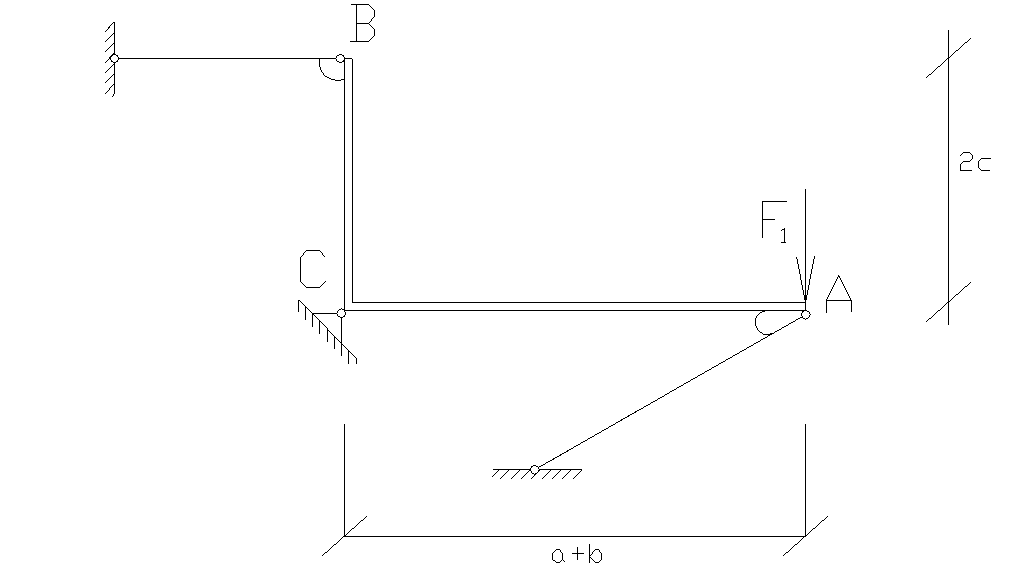
Решение

1.  Статическая сторона. Запишем для данной системы уравнения статики.

 

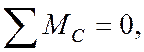
-3,2N₂  – 175 – 3,5N₁=0

2.  Геометрическая сторона. Рассмотрим систему в деформированном состоянии.

          

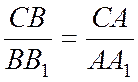
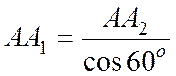
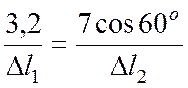
3.  Физическая сторона. Используя закон Гука, выразим удлинение ∆₁ и ∆₂ через неизвестные усилия N₁ и N₂ :

                      

-

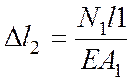
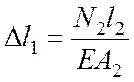
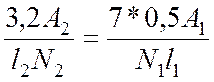
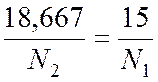
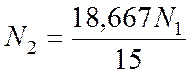
4.  Определим нормальное напряжение:

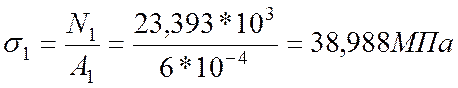
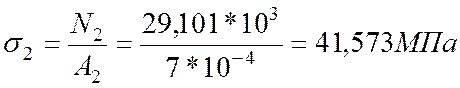
5.  Определим значение допускаемой силы :

6.   

Пусть N₁ = N_adm, тогда N₂ = 1,244*N₁ = 156,744кН

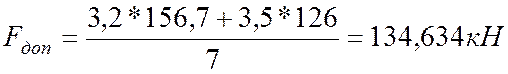
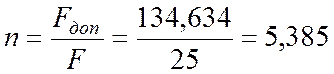  => нагрузку можно увеличить в 5,385 раза.

Задача 2.1. Геометрические характеристики плоских сечений.

Задано сечение, состоящее из прямоугольников (листов) и прокатных профилей

Требуется:

1.  Определить положение центра тяжести;

2.  Определить осевые и центробежные моменты инерции относительно центральных осей;

3.  Определить положение главных центральных осей;

4.  Вычислить значение главных центральных моментов инерции;

5.  Вычертить сечение на миллиметровой бумаге в удобном масштабе и показать все необходимые оси и размеры.

Лист: b₁=1,8см ;  h₁=24см

Двутавр: h₂=220мм ; b₂=110мм ; A₂=30,6см² ; J_x=2550 см⁴ ;J_y=157см⁴

Уголок: h₃=125мм ; b₃= 80мм ; x_c=1,84см ; y_c=4,05см ; A₃=15,98см² ; J_x= 255,62см⁴ ; J_y=80,95см⁴ ; J_min=48,82см⁴

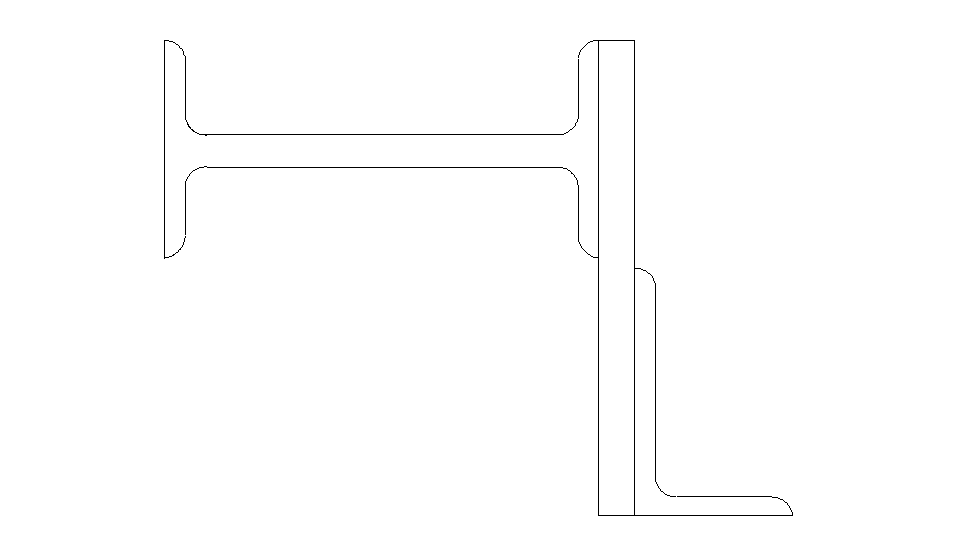
Решение

1.  Определим положение центра тяжести сечения:

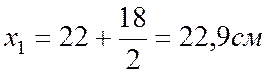
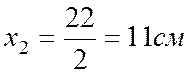
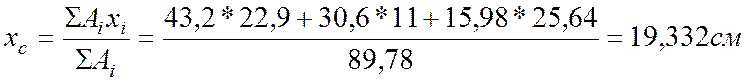
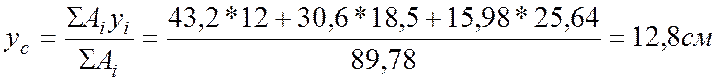
Проверка:

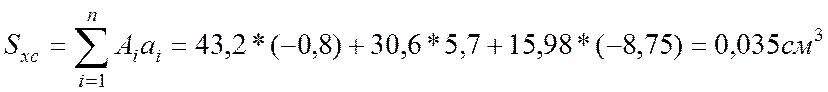
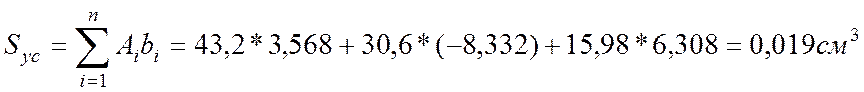
2.  Определим моменты инерции относительно центральных осей.

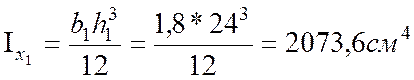
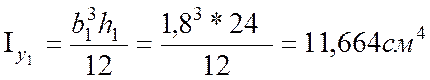
Так как двутавр перевернут, то