Распространение мириаметровых и километровых радиоволн

 

13.1.  Особенности распространения  мириаметровых

 и километровых радиоволн

Исследуются физические особенности распространения мириаметровых и километровых радиоволн.

 

Радиоволны очень низких и низких частот (соответственно называемые мириаметровыми и километровыми волнами) занимают диапазон частот 3∙10⁴ – 3∙10⁵ Гц (НЧ) и 3∙10³ – 3∙10⁴ Гц (ОНЧ). Эти частоты соответствуют длинам волн от 10⁵ до 10³ м. Применительно к радиовещанию радиоволны этого диапазона традиционно называются также сверхдлинными (СДВ) и длинными волнами (ДВ). Для удобства в дальнейшем будем придерживаться последней терминологии.

В пределах всего диапазона модуль отношения плотности тока проводимости к плотности тока смещения в почве много больше единицы, благодаря чему поверхность Земли ведет себя как высокопроводящая среда. По этой причине длинные и сверхдлинные волны испытывают лишь незначительное проникновение в глубь Земли при распространении вдоль ее поверхности.

Благодаря большой длине эти волны хорошо огибают сферическую поверхность Земли, и их распространение описывается законами дифракции. Как следует из рис.13.1., препятствием для поверхностной волны является сегмент, ограниченный хордой АВ.

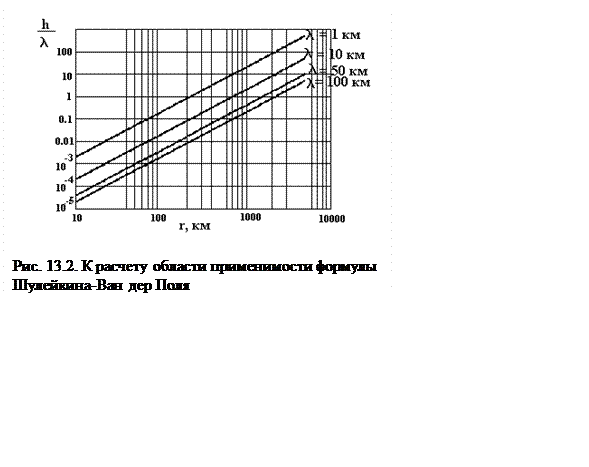
Если отношение высоты сегмента к длине волны много меньше единицы, то кривизной Земли можно пренебречь, и расчет множителя ослабления вести по формуле Шулейкина – Ван дер Поля (13.1). В противном случае расчет прово-дится с учетом сферичности Земли.

Определим область применимости формулы Шулейкина – Ван дер Поля. Относительная высота сегмента  (рис. 13.1.) определяется из формулы:

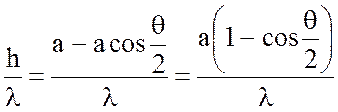,            (13.1)

где  θ – геоцентрический угол, который можно определить из формулы:

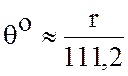                     ,                                          (13.2)

где  а – радиус Земли, r – в км.

На рис. 13.2. приведены результаты расчета относительной высоты сегмента  h  для радиотрасс различной протяженности в диапазоне длин волн от 10³ м до 10⁵ м, откуда следует, что область применимости формулы Шулейкина – Ван дер Поля в зависимости от длины волны колеблется от 100 до 800 км.

.

Начиная с расстояний 300 – 400 км, кроме поверхностной волны, присутствует волна, отраженная от ионосферы. Отсутствие ионосферной волны на более близком расстоянии от передатчика определяется диаграммой направленности передающей антенны в вертикальной плоскости, которая с достаточной точностью повторяет форму диаграммы направленности диполя Герца (рис.13.3.).

Для отражения от ионосферы длинных и сверхдлинных волн требу-ется электронная концентрация, не превышающая величины 10³ эл/см³. Поэтому в дневное время эти волны способны отражаться от нижней границы слоя D, а в ночное время – от нижней границы слоя Е, не проникая в глубь слоя и не испытывая при этом значительного поглощения.

С увеличением расстояния доля ионосферной волны увеличивается, и на расстоянии около 700 – 1000 км поля поверхностной и пространственной волн становятся примерно равными. На расстоянии свыше 3000 км пространственная волна приобретает доминирующее значение.

Испытывая незначительное поглощение в почве и ионосфере, пространственная волна распространяется между двумя полупроводящими поверхностями как в сферическом диэлектрическом волноводе. Как и во всяком волноводе, для этих волн существует критическая длина волны. Она имеет тот же порядок, что и высота нижней границы отражающего слоя, т.е. около 100 км. Таким образом, волны с длиной свыше 100 км между поверхностью Земли и ионосферой распространяться не могут.

Сферическая форма волновода вызывает особенность распространения, известную как “эффект антипода”. Этот эффект заключается в возрастании напряженности поля в точке, расположенной на противоположном конце диаметра Земли, проведенного через передающую антенну. Первоначально рассмотрим случай (рис.13.4.), когда обе стенки волновода являются идеально проводящими.

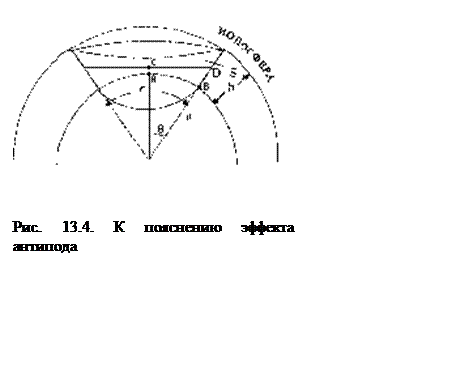Предположим, что плотность потока энергии волны постоянна по всей высоте волновода. Учитывая, что в диапазоне длинных и сверхдлинных волн применяются антенны, не имеющие направленных свойств в горизонтальной плоскости, запишем выражение для вектора Пойнтинга в точке В: