

ВАРИАНТ В.4-2.
Задание.
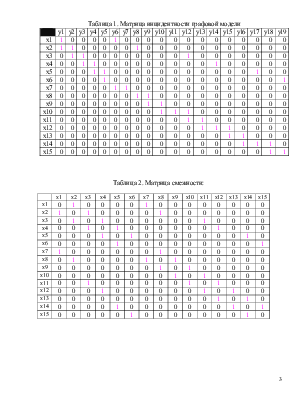
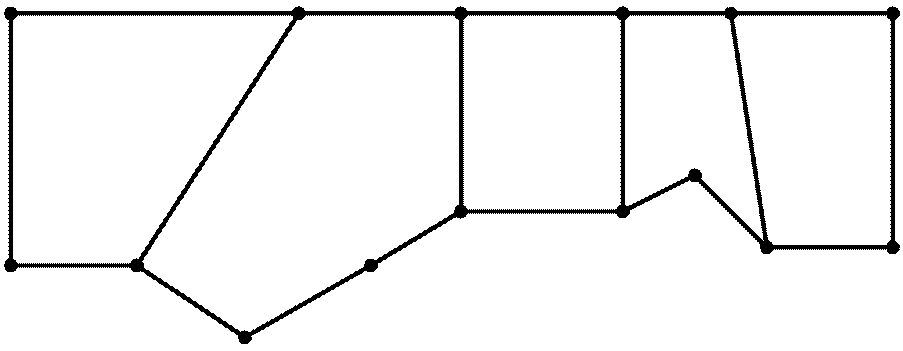
1) Построить матрицу инцидентности и смежности для графовой модели (рис.1)
2) Определить основный метрические характеристики будущей СЭГ:
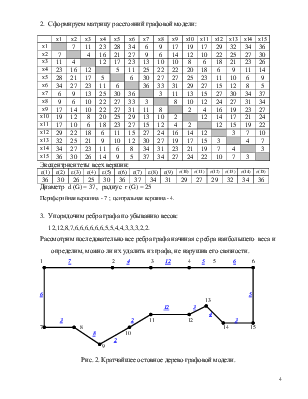
a) Построить матрицу расстояний
b) Определить эксцентриситеты всех вершин.
c) Определить радиус и диаметр модели сети.
d) Определить центральные и периферийные вершины графовой модели.
3) По алгоритму Прима-Краскала построить кратчайшее остовное дерево с минимальным весом ребер.
Решение.
1 7 2 4 3 12 4 5 5 6 6
6 6 6 6 6 5
13
12 3
4
3 2 11 12 3
7 8 14 15
8 10
2
9
Рис. 1.
1. Обозначим вершины графа х1, х2, …х15.
Ребра графа: у1=1-2 вершина, у2=2-3 вершина, у3=3-4 вершина, у4=4-5 вершина, у5=5-6 вершина, у6=1-7 вершина, у7=7-8 вершина, у8=2-8 вершина, у9=8-9 вершина, у10=9-10 вершина, у11=10-11 вершина, у12=11-3 вершина, у13=11-12 вершина, у14=12-4 вершина, у15=12-13 вершина, у16=13-14 вершина, у17=5-14 вершина, у18=14-15 вершина, у19=15-6 вершина, (на рисунке обозначен вес ребер).
Построим матрицу инцидентности:
|
Таблица 1. Матрица инцидентности графовой модели |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.