Построение матрицы инцидентности и смежности для графовой модели. Построение матрицы расстояний, страница 3

	х1	х2	х3	х4	х5	х6	х7	х8	х9	х10	х11	х12	х13	х14	х15
х1		7	11	23	28	34	6	9	17	19	17	29	32	34	36
х2	7		4	16	21	27	9	6	14	12	10	22	25	27	30
х3	11	4		12	17	23	13	10	10	8	6	18	21	23	26
х4	23	16	12		5	11	25	22	22	20	18	6	9	11	14
х5	28	21	17	5		6	30	27	27	25	23	11	10	6	9
х6	34	27	23	11	6		36	33	31	29	27	15	12	8	5
х7	6	9	13	25	30	36		3	11	13	15	27	30	34	37
х8	9	6	10	22	27	33	3		8	10	12	24	27	31	34
х9	17	14	10	22	27	31	11	8		2	4	16	19	23	27
х10	19	12	8	20	25	29	13	10	2		12	14	17	21	24
х11	17	10	6	18	23	27	15	12	4	2		12	15	19	22
х12	29	22	18	6	11	15	27	24	16	14	12		3	7	10
х13	32	25	21	9	10	12	30	27	19	17	15	3		4	7
х14	34	27	23	11	6	8	34	31	23	21	19	7	4		3
х15	36	30	26	14	9	5	37	34	27	24	22	10	7	3

Эксцентриситеты всех вершин:

e(1)	e(2)	e(3)	e(4)	e(5)	e(6)	e(7)	e(8)	e(9)	e(10)	e(11)	e(12)	e(13)	e(14)	e(15)
36	30	26	25	30	36	37	34	31	29	27	29	32	34	36

Диаметр  d (G) = 37,   радиус  r (G) = 25

Периферийная вершина  - 7 ;  центральная вершина - 4.

3.  Упорядочим ребра графа по убыванию весов: 12,12,8,7,6,6,6,6,6,6,5,5,4,4,3,3,3,2,2.

Рассмотрим последовательно все ребра графа начиная с ребра наибольшего  веса и 

       определим, можно ли их удалить из графа, не нарушив его связности.

1                  7                             2        4               3        12            4        5      5            6           6

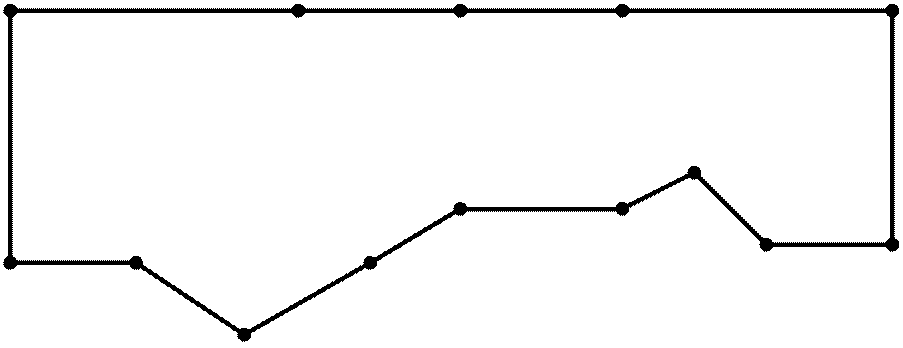
6                                                                                                                                                 5

                                                                                                                    13                              

                                                                                       12                 3

                                                                                                                       4       

              3                                                2           11                       12                             3

7                          8                                                                                                   14               15

                                     8                     10

                                                    2

                                            9

Рис. 2. Кратчайшее остовное дерево графовой модели.

Суммарный вес ребер  Σvреб =  82

Литература.

1.  Конспект лекций.