Определение системных характеристик цепи. Определение сигнала на выходе цепи. Расчет масштабного множителя на входе цепи

Министерство  РФ по Связи и Информатизации

Сибирский Государственный Университет Телекоммуникаций и Информатики

Кафедра ТЭЦ                      

ДОМАШНЯЯ РАБОТА  ПО КУРСУ ЦОС

Выполнил: 

       Проверил:

Новосибирск   2003

Исходные данные:

a₀ = -0,1;     

а₁ =  0;         b₁ = -0,5;

а₂ =  0,5;      b₂ =  0,16;

 x(nT) = {0,6; 0,5; 0,1};

Часть I

Определение системных характеристик цепи

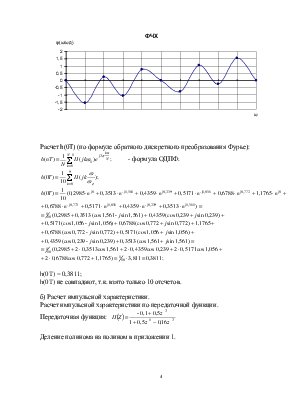
а) Определить передаточную функцию (проверить устойчивость цепи) рассчитать АЧХ и ФЧХ цепи с шагом  f₁ = f_д / 10. Построить графики АЧХ и ФЧХ.

Вычислить h(0Т).

Передаточная функция:

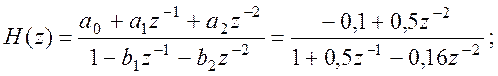
Полюсы передаточной функции:

1+ 0,5 z ^–1 – 0,16 z ^{– 2}  = 0;  

z ² + 0,5 z – 0,16 = 0; 

D = b²  – 4ac = 0,25 + 0,64 = 0,89;

z_1,2  = -0,5 ± 0,943;

z₁ =  0,2217;    z₂ = -0,7217;

Т.к. корни знаменателя лежат в единичной окружности,  то схема устойчива.

Расчет АЧХ и ФЧХ цепи.

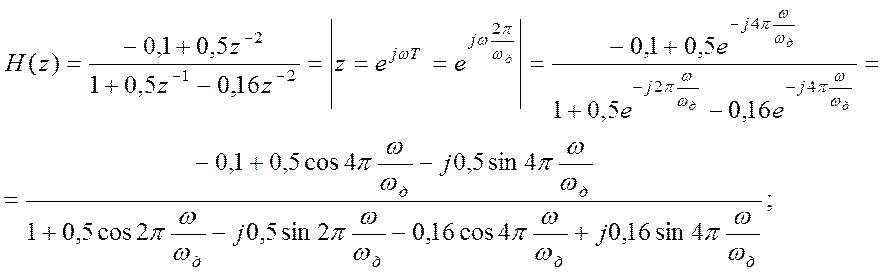
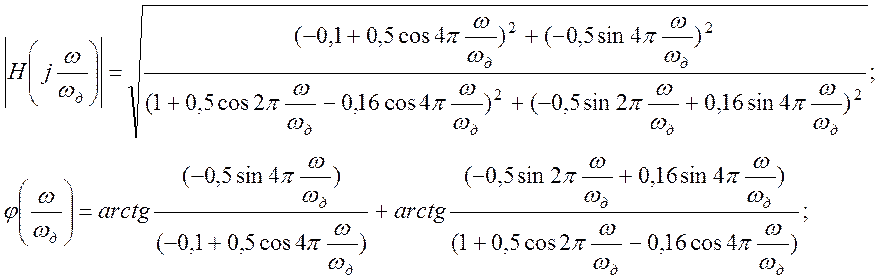
ω	0	0,1ωд	0,2ωд	0,3ωд	0,4ωд	0,5ωд	0,6ωд	0,7ωд	0,8ωд	0,9ωд	1ωд
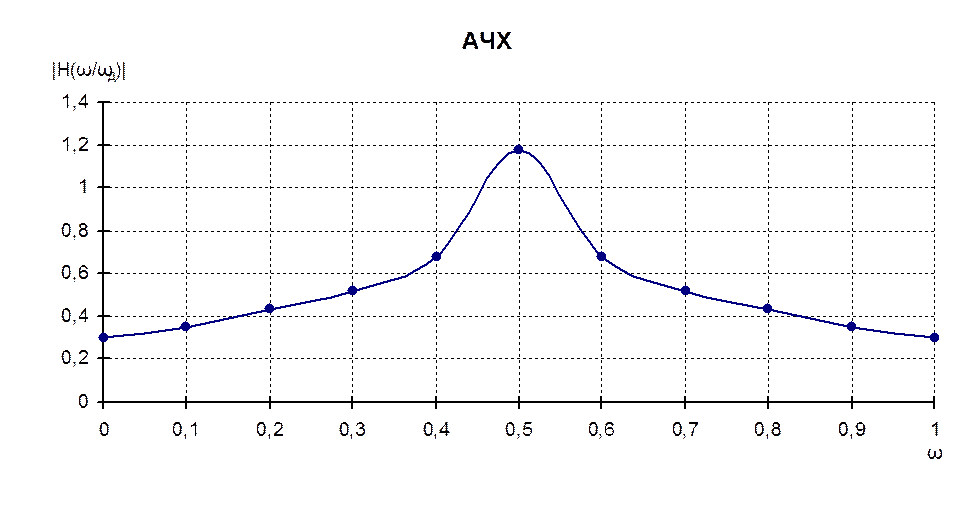
|H(jω/ωд)|	0,2985	0,3513	0,4359	0,5171	0,6788	1,1765	0,6788	0,5171	0,4359	0,3513	0,2985
φ(ω/ωд)	0	-1,561	0,239	-1,056	0,772	0	-0,772	1,056	-0,239	1,561	0

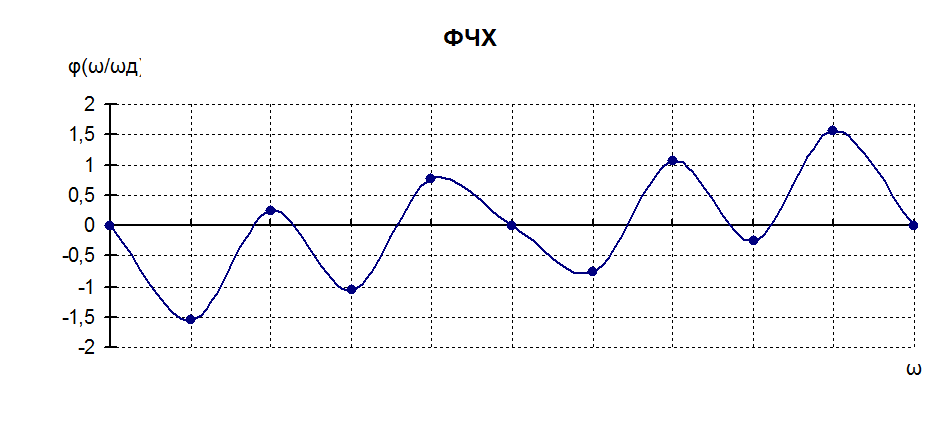
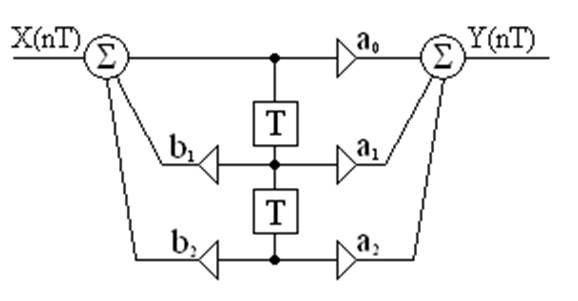
Расчет h(0T) (по формуле обратного дискретного преобразования Фурье):

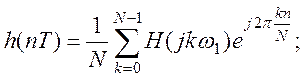          - формула ОДПФ.

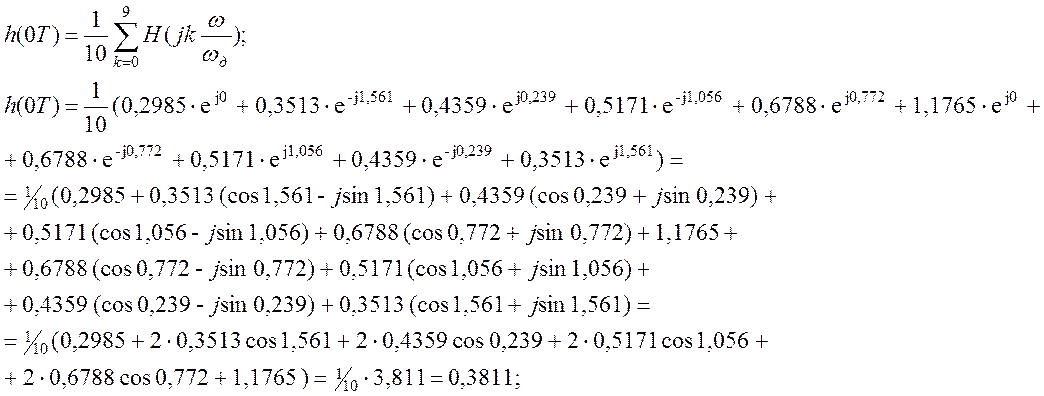
h(0T) = 0,3811;

h(0T) не совпадают, т.к. взято только 10 отсчетов.

б) Расчет импульсной характеристики.

Расчет импульсной характеристики по передаточной функции.

Передаточная функция: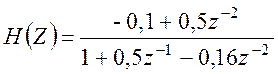 

Деление полинома на полином в приложении 1.

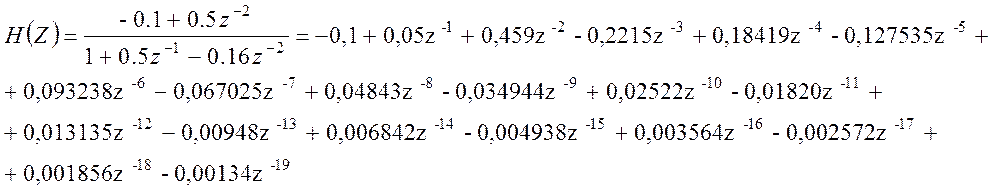
в результате импульсная характеристика:

 h(nT) = {-0,1; 0,05; 0,459; -0,2215; 0,18419; -0,127535; 0,093238; -0,067025; 0,04843;

-0,034944; 0,02522; -0,01820; 0,013135; -0,00948; 0,00684;

-0,004938; 0,003564; -0,002572; 0,001856; -0,00134};

Расчет импульсной характеристики по разностному уравнению.

 H(z) =   Y(z) / X(z);

Y(z)(1 + 0,5z ^-1 - 0,16z ^-2 ) = X(z)(- 0,1 + 0,5z ^-2 );

Y(z) + 0,5Y(z) z ^-1 - 0,16Y(z) z ^-2 = - 0,1X(z) + 0,5X(z) z ^-2;

z-изображение разностного уравнения:

Y(z) = - 0,5Y(z) z ^-1 + 0,16Y(z) z ^-2 - 0,1X(z) + 0,5X(z) z ^-2;

Y(z) => y(nT);

Разностное уравнение:

y(nT) = - 0,5y(nT – T) + 0,16y(nT – 2T) - 0,1x(nT) + 0,5x(nT – 2T);

Если на вход схемы подать δ – функцию (δ = {1,0,0,0,0,…}), то на выходе будет импульсная характеристика цепи.

y(nT) = - 0,5y(nT – T) + 0,16y(nT – 2T) - 0,1 δ (nT) + 0,5 δ (nT – 2T);

Так как на входе δ – функция, то только δ (0Т) = 1, все остальные отсчеты

δ – функции равны нулю.

n = 0;

y(0T) = - 0,5y(0T – T) + 0,16y(0T – 2T) - 0,1δ(0T) + 0,5δ(0T – 2T) =

= - 0,5y(– T) + 0,16y(– 2T) - 0,1δ(0T) + 0,5δ(– 2T) = - 0,1;

n = 1;

y(1T) = - 0,5y(1T – T) + 0,16y(1T – 2T) - 0,1δ (1T) + 0,5δ(1T – 2T) =

= - 0,5y(0T) + 0,16y(– 1T) - 0,1δ(1T) + 0,5δ(– 1T)  = -0,5*-0,1  = 0,05;

n = 2;

y(2T) = - 0,5y(2T – T) + 0,16y(2T – 2T) - 0,1δ(2T) + 0,5δ(2T – 2T)  =

= - 0,5y(1T) + 0,16y(0T) - 0,1δ(2T) + 0,5δ(0T)  = -0,5*0,05  + 0,16*-0,1 + 0,5 = 0,459;

n = 3;

y(3T) = - 0,5y(3T – T) + 0,16y(3T – 2T) - 0,1δ(3T) + 0,5δ(3T – 2T) =

= - 0,5y(2T) + 0,16y(1T) - 0,1δ(3T) + 0,5δ(1T) = -0,5 * 0,459 + 0,16*0,05 = -0,2215;

n = 4;

y(4T) = - 0,5y(4T – T) + 0,16y(4T – 2T) - 0,1δ(4T) + 0,5δ(4T – 2T) =

= -0,5y(3T) + 0,16y(2T) - 0,1δ(4T) + 0,5δ(2T) = -0,5*-0,2215 + 0,16*0,459 = 0,18419;

n = 5;

y(5T) = - 0,5y(5T – T) + 0,16y(5T – 2T) - 0,1δ(5T) + 0,5δ(5T – 2T) =

= - 0,5y(4T) + 0,16y(3T) - 0,1δ(5T) + 0,5δ(3T) = -0,5*0,18419 + 0,16*-0,2215 = -0,127535;

n = 6;

y(6T) = - 0,5y(6T – T) + 0,16y(6T – 2T) - 0,1δ(6T) + 0,5δ(6T – 2T) =

= - 0,5y(5T) + 0,16y(4T) - 0,1δ(6T) + 0,5δ(4T) = -0,5*-0,127535 +0,16*0,18419 = 0,093238;

n = 7;

y(7T) = - 0,5y(7T – T) + 0,16y(7T – 2T) - 0,1δ(7T) + 0,5δ(7T – 2T)  =

= - 0,5y(6T) + 0,16y(5T) - 0,1δ(7T) + 0,5δ(5T) = -0,5*0,093238 + 0,16*-0,127535 = -0,067025;

n = 8;

y(8T) = - 0,5y(8T – T) + 0,16y(8T – 2T) - 0,1δ(8T) + 0,5δ(8T – 2T)  =

= - 0,5y(7T) + 0,16y(6T) - 0,1δ(8T) + 0,5δ(6T) = -0,5*-0,067025 + 0,16*0,093238 = 0,04843;

n = 9;

y(9T) = - 0,5y(9T – T) + 0,16y(9T – 2T) - 0,1δ(9T) + 0,5δ(9T – 2T)  =

= - 0,5y(8T) + 0,16y(7T) - 0,1δ(9T) + 0,5δ(7T) = -0,5*0,04843 + 0,16*-0,067025 = -0,034939;

n = 10;