Определение параметра ФПВ. Построение ФПВ и функции распределения вероятностей случайного процесса

Задача1.

            Стационарный случайный процесс x(t) имеет одномерную функцию плотности вероятности (ФПВ) мгновенных  значений w(x), график и параметры которой приведены на рисунке1.

            Требуется:

1. Определить параметр h ФПВ.

2. Построить ФПВ w(x) и функцию распределения вероятностей (ФРВ) F(x) случайного процесса.

3. Определить первый m₁ (математическое ожидание) и второй m₂ начальные моменты, а также дисперсию D(x) случайного процесса.

1)

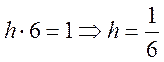
                                                               0.3·δ(x-3)          0.15·δ(x-6)

      

                                             h     

                                                           2          3                   6             8           

рис.1ФПВ

2)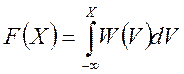  –∞<X<∞,

++

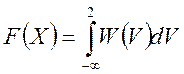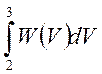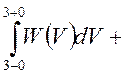
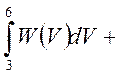
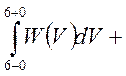
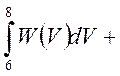
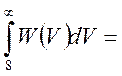
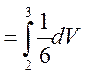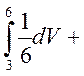
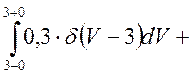
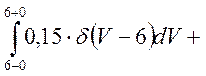
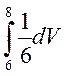+=1

                                               Рис 2. ФРВ

3)  m₁==+ ++++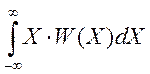

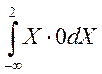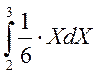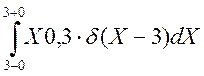
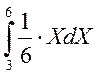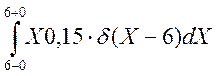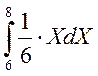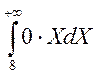+= 5

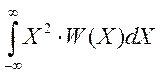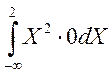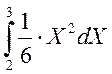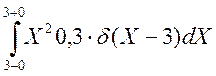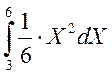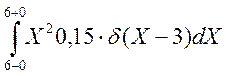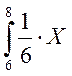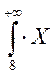m₂==+  + +++²+ ²= 28

D=(m₁-X)² W(X)dX=-X)²0dX+(5-X)²dX+(5-X)² 0dX = 3

Задача 2.

Энергетический спектр гауссовского стационарного  случайного процесса x(t) равен

G (ω)=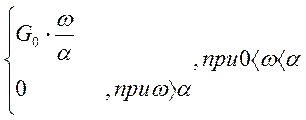  

где 400 рад/с, G₀= 6 ∙10^-3 В²с/рад      .

 Среднее значение случайного процесса равен  m_x=m₁=M= – 3.

Требуется:

1. Определить корреляционную функцию B(τ) случайногопроцесса.

2. Рассчитать величины эффективной ширины спектра и интервала корреляции рассматриваемого процесса.

3. Изобразите графики G(ω) и B(τ) с указанием масштаба по осям и покажите на них эффективную ширину спектра и интервал корреляции.

4. Запишите выражение для функции плотности вероятности w(x) гауссовского стационарного случайного процесса и постройте её график.

5. Определите вероятности того, что мгновенные значения случайного процесса будут меньше a–p(x<a); будут больше b–p(x>b); будут находиться внутри интеграла [c,d]–p(c<x<d),

Где a= –5; b= 0,5; c= –4; d= –1,5.

1) G(ω)= 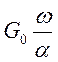 , при 0 < ω <α–    энергетический спектр ГССП

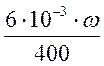G(ω)=,    при 0 < ω <α

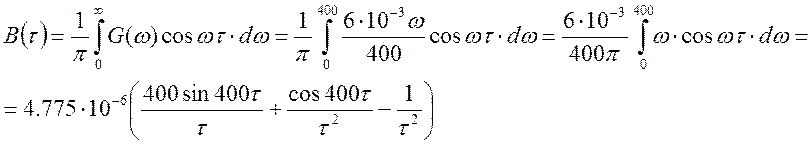
2)

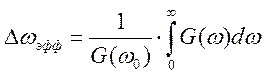
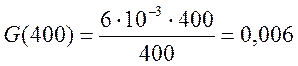
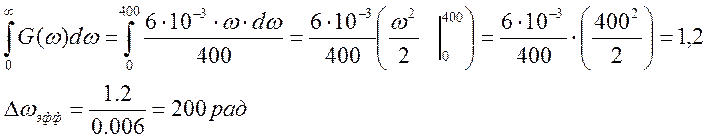
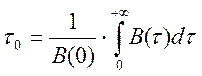
В(0) = 0,384

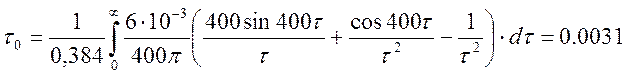
3)  Графики B(τ), G(ω).

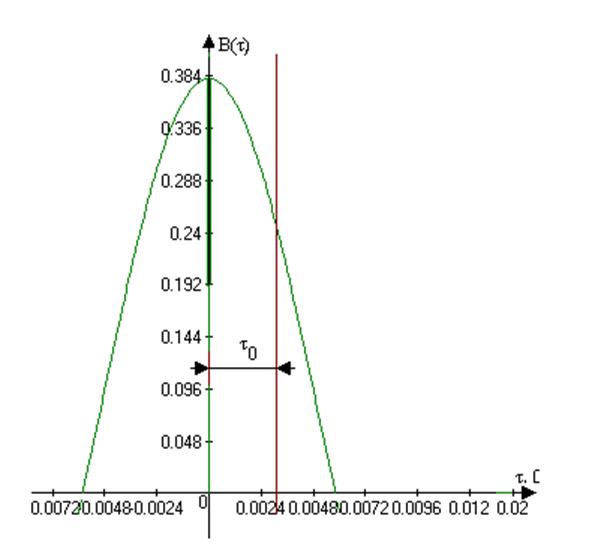
                                    Рис3. Корреляционная функция B(τ)

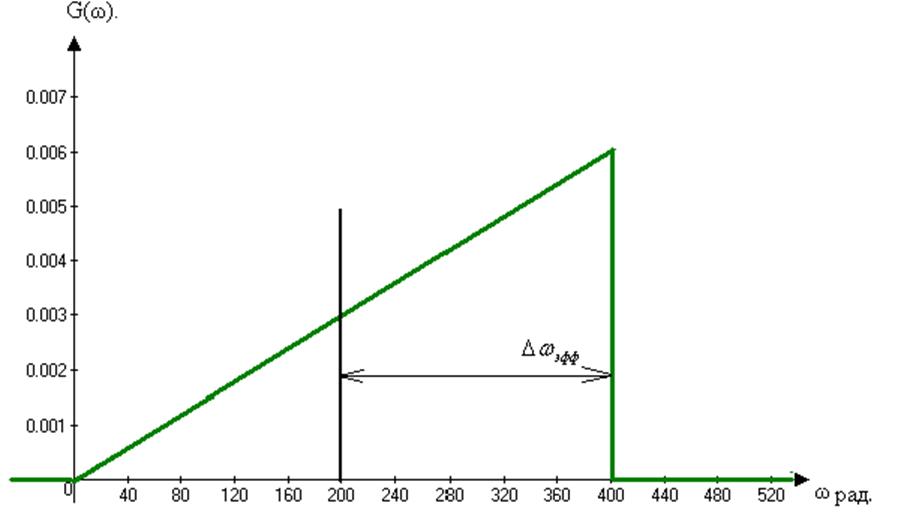
                                               Рис4.Энергетический спектр G(ω).

4)

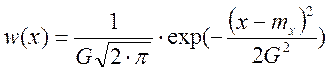
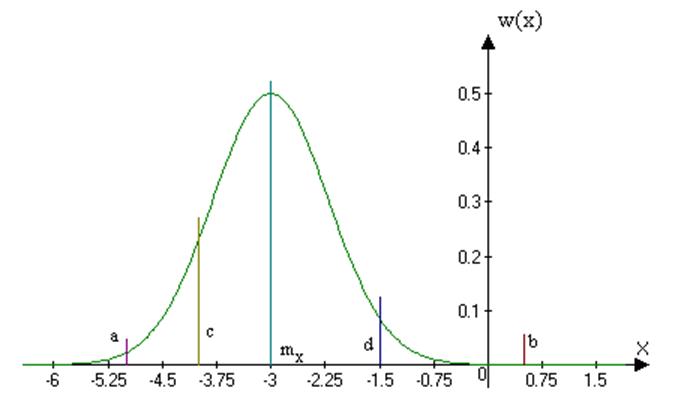
                                    Рис5. Функция плотности вероятности w(x)

5)

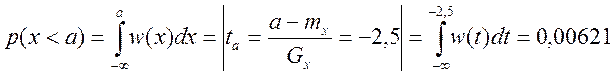
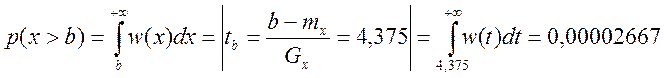
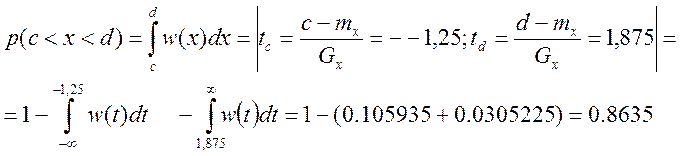
Задача3.

            Вольт-амперная характеристика (ВАХ) биполярного транзистора амплитудного модулятора аппроксимирована выражением:

i_к =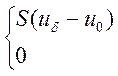          при                      <

где i_к – ток коллектора транзистора;

       u_б – напряжение на базе транзистора;

       S – крутизна вольт-амперной характеристики;

       u₀ – напряжение отсечки ВАХ

Требуется:

1. Объяснить назначение модуляции несущей и описать различные виды модуляции.
2. Изобразить схему транзисторного амплитудного модулятора, пояснить принцип ее работы и назначение ее элементов.
3. Дать понятие статической модуляционной характеристики (СМХ). Рассчитать и построить (СМХ) при заданных S, u₀ и значении амплитуды входного высокочастотного напряжения U_m.
4. С помощью статической модуляционной характеристики определить оптимальное смещение E₀ и допустимую величину амплитуды Uмодулирующего напряжения Ucost, соответствующие неискаженной модуляции.
5. Рассчитать коэффициент модуляции m_АМ для выбранного режима. Построить спектр и временную диаграмму АМ-сигнала.

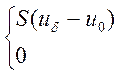i_к =          при                      <           

S = 100 mA/B

u₀ = 0,6 В

u_m= 0,5 В

i_к =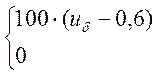    при       0,6         < 0,6

1) Модуляция позволяет переносить низкочастотный спектр информационного сигнала в высокую область частот, появляется возможность частотного разделения каналов – одновременная передача пользовательской информации в различных частотных диапазонах.

            Виды модуляции:

Амплитудная модуляция – изменение амплитуды в. ч. сигнала по закону н.ч. сигнала.

Частотная модуляция – изменение частоты в. ч. сигнала по закону н.ч. сигнала.

Фазовая модуляция – изменение фазы в. ч. сигнала по закону н.ч. сигнала.