Расчёт и проектирование горизонтального газгольдера, страница 4

1.6 Расчёт на прочность сопряжения плоского днища со стенкой

Нормальное радиальное напряжение на контуре днища равно

,

где Коэффициент  определён, как для мембраны с несмещающимся контуром, сравнивая значения напряжений в центре и по контуру.

.

Часть напряжений воспринимается кольцом жёсткости, а другая часть – цилиндрической оболочкой (стенкой) в зоне центра тяжести сечения кольца жёсткости:

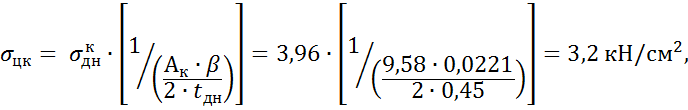
где 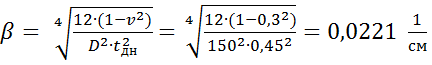- коэффициент деформации днища.

Вследствие внецентренного приложения усилия  от днища в зоне сопряжения днища со стенкой возникает изгибающий момент.

,

где е =  = 1,67 см.

= =  = 2,4 кН.

Нормальные напряжения в стенке (и в днище тоже) от момента  значительны. При этом не учитывается влияние момента краевого эффекта, аналогичного моменту в зоне сопряжения стенки с днищем вертикального цилиндрического резервуара, который снижает действие .

1.7 Проверка на прочность стенки и днища резервуара в узле их сопряжения

Напряжение в стенке без учёта краевого эффекта (t_cт = 4 мм)

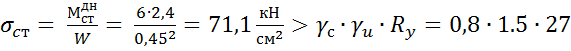= 32,4  - прочность стенки не обеспечена.

Напряжение в днище

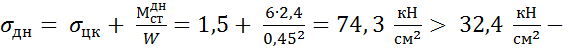прочность днища не обеспечена в этой зоне. Следует плоское днище укрепить рёбрами жёсткости.

Вычислим в зоне сопряжения днища со стенкой изгибающий момент краевого эффекта М₀. Предварительно найдём коэффициенты и свободные члены канонического уравнения метода сил:

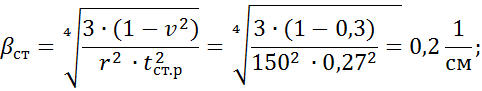
 = 0,25 ;

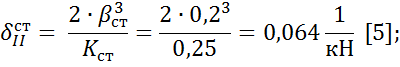
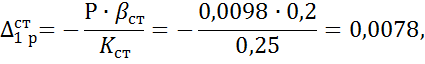
где P =

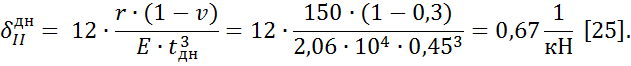
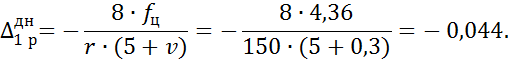
Подставляем полученные значения в уравнение

, отсюда М₀ = 0,071 кН.

Суммарный изгибающий момент в зоне краевого эффекта

Проверим стенку резервуара на прочность в зоне краевого эффекта без учёта меридиональных напряжений, величина которых незначительна

.

Прочность стенки резервуара в зоне краевого эффекта недостаточна. Однако если принять кольцо жёсткости днища в соответствии с (рис 2), то и остаётся только М₀. При этом

 то есть прочность стенки обеспечена.

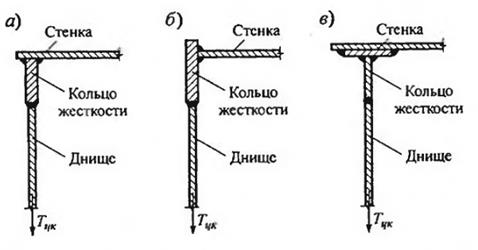
Рисунок 3 – Рациональные типы сечений кольца жёсткости

Проверим на прочность вариант плоско-ребристого днища толщиной t_дн = 5 мм.

Конструкцию плоско-ребристого днища примем, как показано на рис.

Ребро- пластина толщиной 10 мм и шириной .

Расстояние между рёбрами по краю днища:

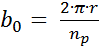== 39,25 см.

Расчётный пролёт полоски днища

.

Стрелу прогиба единичной ширины полоски днища, как изгибно-жёсткой нити, при расчётном давлении P_u = 5,5∙ кН/см² и расчётной толщине днища t_дн.р = 4,5 мм приближённо можно определить по формуле

.

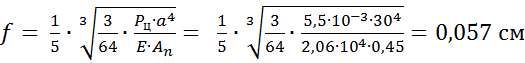Распор изгибно-жёсткой нити

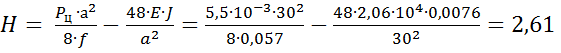кН/см.

Коэффициент

.

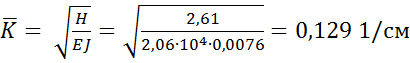Опорный момент полоски единичной ширины (изгибно-жёсткой нити)

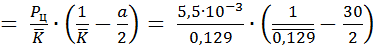  = - 0,309 кН.

Проверка на прочность днища по формуле

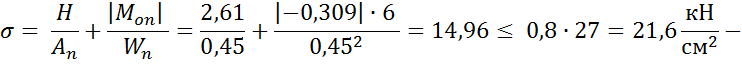
прочность плоского днища с радиальными рёбрами обеспечена.

Стоит заметить, что толщины стенки и днищ резервуара определяются зоной краевого эффекта.

Произведём расчёт кольцевых швов, соединяющих кольцо жёсткость с днищем и со стенкой (рис 3).

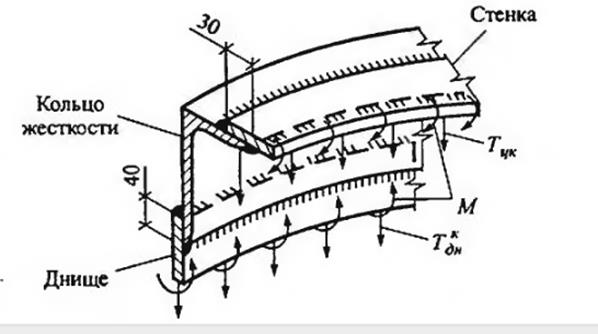
Рисунок 4 - К расчёту кольцевых швов

Кольцевые швы, соединяющие днище с кольцом жёсткости, воспринимают радиальные усилия по контуру днища .

Напряжение в кольцевом шве от

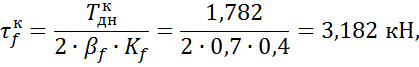
и от момента

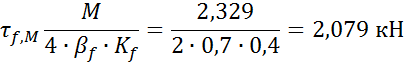
взаимно перпендикулярны; 4 см – расстояние между центрами сечений сварных швов.

Примем полуавтоматическую сварку электродной проволокой маркой С_в-08А (R_wf = 18,0 кН/см²).

Расчётное сопротивление по металлу границы сплавления шва

R_wz = 0,45∙ R_un = 0,45∙380 = 171 МПа.

Примем K_f = 4 мм. Коэффициент проплавления шва:  – для электродной проволоки диаметром менее 1,4 мм.

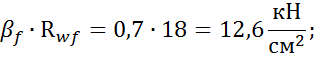
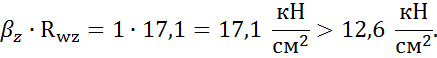
Следовательно, расчётным сечением будет по металлу шва.

Результирующее напряжение в шве

 =18

Кольцевые швы, которые соединяют стенку резервуара с кольцом жёсткости, воспринимают усилие результирующий момент М и сдвигающее усилие Т между кольцом жёсткости и стенкой от гидростатического давления жидкости Т_ж и собственного веса резервуара Т_с.в, то есть

Т = Т_ж + Т_с.в = 0,5/2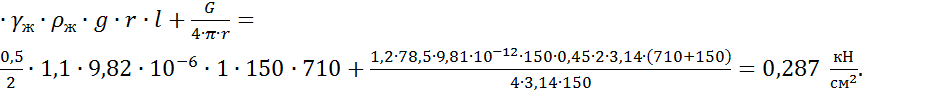

Напряжение в кольцевом шве от

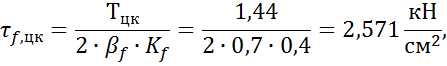
от момента

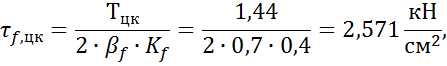
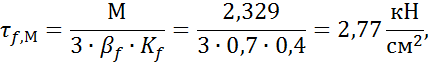
от сдвигающего усилия