Примеры расчетов с использованием корреляционных функций

Примеры расчетов с использованием корреляционных функций

1. Расчет погрешности фильтрации от измерительной помехи

          При автоматическом контроле большое значение имеют задачи фильтрации выходного сигнала датчика, то есть отделение полезного сигнала x(t) от измерительной помехи g(t). В общем случае стоит задача определения статистически оптимального оператора фильтрации , минимизирующего СКО отклонения  оценки

                                                                                     

от полезного сигнала  (см. рисунок)

 

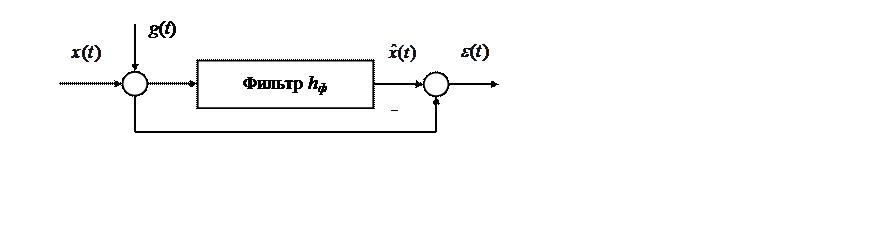
Рис. Схема фильтрации от измерительных помех

          На практике широко распространен способ фильтрации измеряемого сигнала от высокочастотных помех путем вычисления скользящего среднего, когда (см. рис.)

                                                                             

                                       

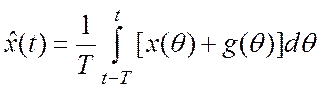
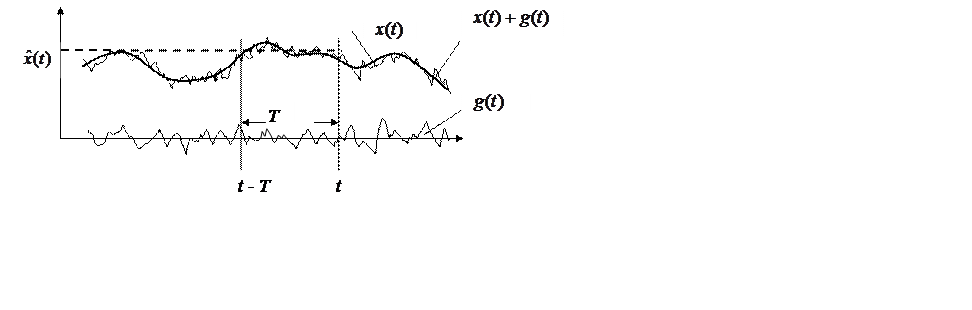
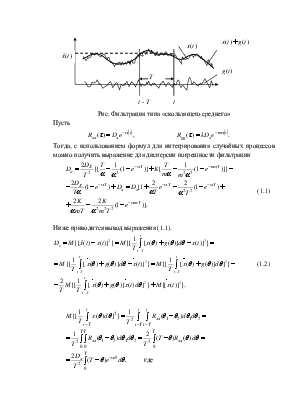
Рис. Фильтрация типа «скользящего среднего»

Пусть

                                

Тогда, с использованием формул для интегрирования случайных процессов можно получить выражение для дисперсии погрешности фильтрации

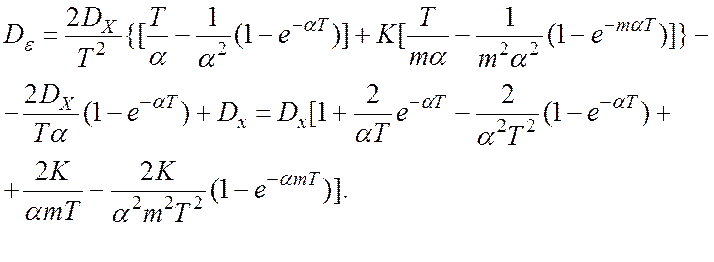                     (1.1)

Ниже приводится вывод выражения (1.1).

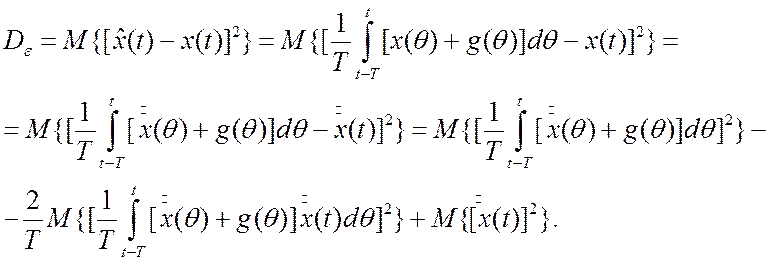             (1.2)

       

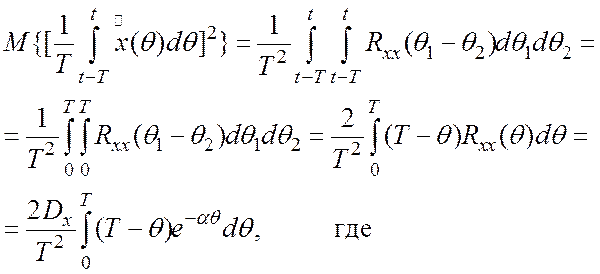
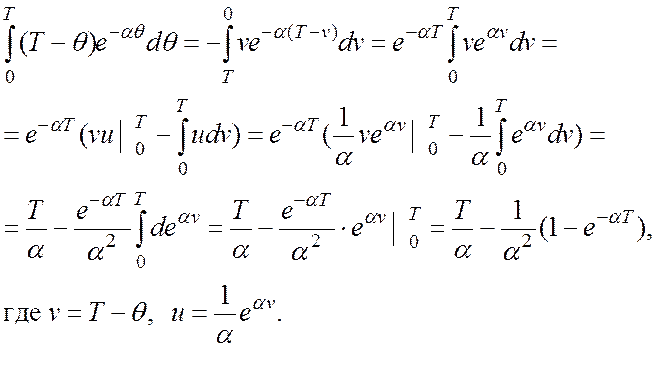                              (1.3)

Аналогично

                  

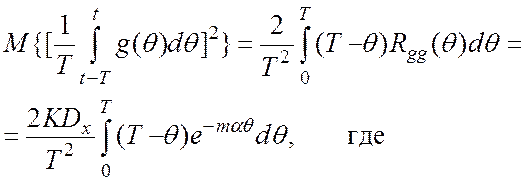
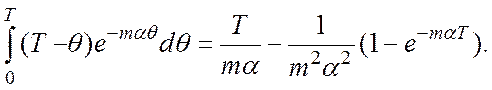                                                   (1.4)

И наконец,

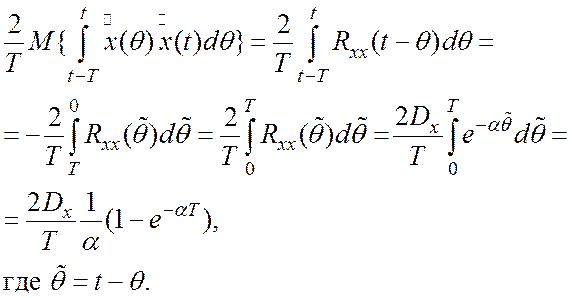                                        (1.5)

Подставляя (1.3), (1.4) и (1.5) в (1.2), получим

         

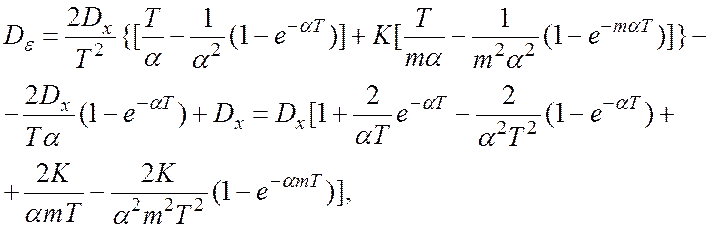
что соответствует (1.1).

Рассмотрим крайние случаи.

    

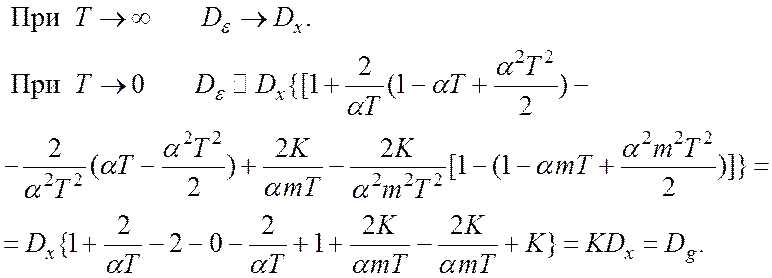
Важно отметить, что в рассмотренных крайних случаях формально полученное решение согласуется с физическим смыслом задачи.

Оптимальное значение интервала усреднения может быть найдено путем минимизации  по .

2. Расчет силы торможения в механической системе

k

          Рассмотрим типовую механическую систему с пружиной и демпфером, которая под действием вынуждающей силы  совершает перемещение .

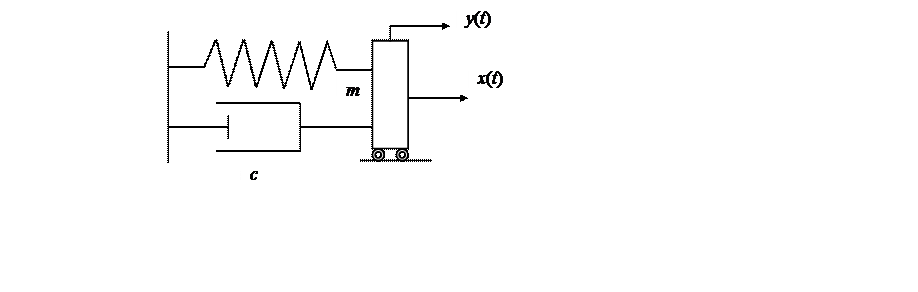
Рис. Механическая система с пружиной и демпфером

Уравнение движения такой системы имеет вид:

                                                                         

На систему действует случайная сила , вызывающая случайное перемещение массы , характеризуемое корреляционной функцией

                             .                         

 

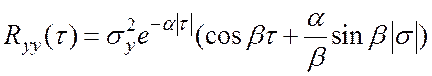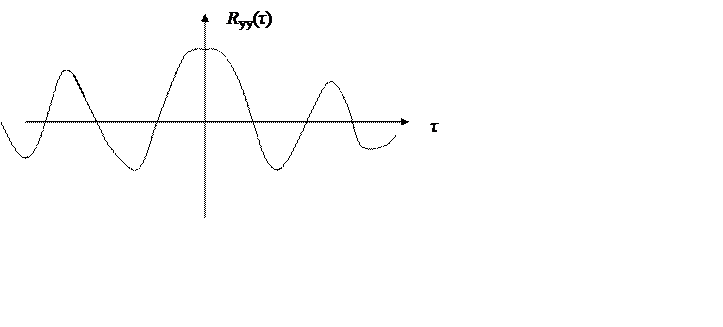Рис. Корреляционная функция случайных перемещений

Необходимо рассчитать среднеквадратическое и максимальное значение тормозящей силы .

Воспользовавшись формулой для дифференцирования случайных процессов, получим:

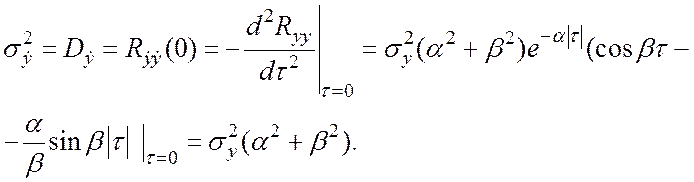                 (2.1)

Таким образом,

                                                                         

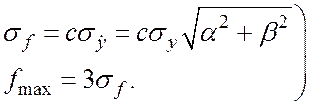
Здесь использовано правило «трех сигм».

Вывод формулы для : Пусть , тогда

      

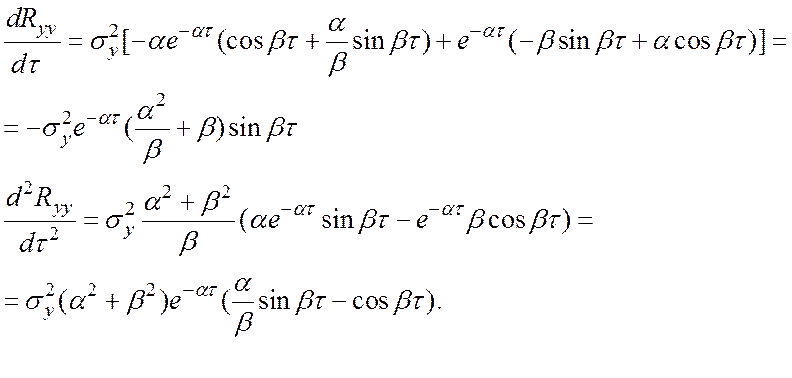
Поскольку для четной функции  функция 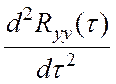 тоже четная, то

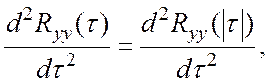 откуда и следует (2.1).