Более корректными представляются измерения, в которых, наряду со скоростью счета, определяется уровень непрерывной АЭ, что позволяет уменьшить неопределенность результатов, обусловленную произвольным выбором уровня дискриминации сигналов. В частности, отмечено, что зависимость уровня АЭ при изменении скорости деформации меняется более плавно, чем скорость счета, имеющая максимум, который тем уже, чем выше уровень дискриминации. С учетом сказанного, можно охарактеризовать закономерности проявления АЭ при пластическом деформировании следующим образом.
Характер АЭ зависит от вида движения дислокаций. Если движение дислокаций однородно и непрерывно в объеме исследуемого материала, то большое количество малых импульсов создает непрерывную АЭ. При пространственной или временной неоднородности деформации проявляются вспышки большой амплитуды. Общепринято, что появлению АЭ-сигналов с большой амплитудой способствуют высокая скорость деформирования, гетерогенность материала, склонность его к хрупкому разрушению и деформации двоиникованием, кристаллографическая структура с ограниченным числом систем скольжения (тетрагональная, кубическая, гексагональная), крупнозернистая структура образца. Напротив, непрерывная АЭ с малым уровнем возникает в гомогенных мелкозернистых материалах при малой скорости деформирования сдвигом, что присуще, в частности, материалам с изотропной кристаллической структурой. Изменение условий деформирования (температуры, приложенных напряжений, среды) приводит к изменению соотношения между активностями двух видов АЭ.
Для непрерывной АЭ характерно проявление эффекта Кайзера, заключающегося в отсутствии АЭ при повторном нагружении объекта до ранее достигнутых напряжений. Практически АЭ при повторном нагружении начинает проявляться несколько раньше, чем достигается первоначальный уровень напряжений, а полностью восстанавливается несколько позже достижения этого уровня. Отжиг образца после первичного деформирования нарушает эффект Кайзера, с возрастанием степени отжига увеличивается степень восстановления характеристик АЭ-сигналов. При полном отжиге АЭ восстанавливается до первоначального уровня.
Эффект Кайзера не наблюдается при возникновении трещин, так как в этом случае средняя по объему образца деформация не характеризует деформацию отдельных его областей из-за наличия концентраторов напряжений и активации трещин. При повторном нагружении деформация вблизи вершин трещин может превзойти ранее достигнутую, что приведет к появлению АЭ.
При первичном нагружении материала наблюдается изменение активности АЭ, характеризующееся диаграммами, представленными на рисунке 4.1. Диаграммы соответствуют различному характеру и разным механизмам пластического деформирования.
Диаграмму 4.1, а обычно связывают с ростом числа подвижных дислокаций на начальной стадии пластического деформирования. При последовательном увеличении напряжения (и деформации) сначала активируется большое число дислокационных сегментов малой длины. Затем увеличивается характерная длина сегментов и их распределение становится таким, что упругая энергия, излучаемая освобождающимися дислокациями, достигает максимума. Дальнейший рост деформации приводит к уменьшению длины сегментов из-за их многочисленности и к соответствующему уменьшению амплитуды возникающих АЭ-сигналов. Предпринимались попытки количественного описания связи.
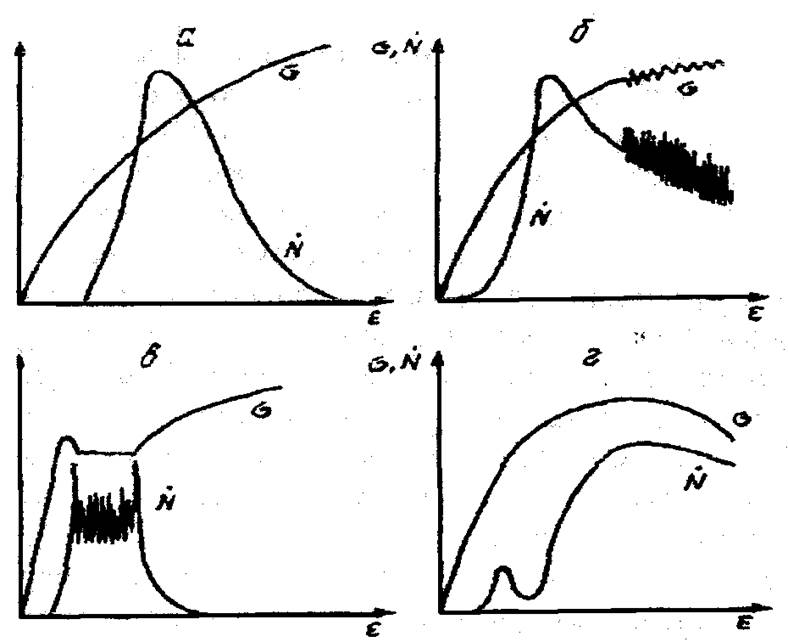
Рисунок 4.1 - Диаграммы, характеризующие акустическую эмиссию при пластической деформации материалов по различным механизмам:
а - при росте числа подвижных дислокаций на начальной стадии пластической деформации; б - по деформации по механизму Чернова-Людерса; в - при наличии зуба текучести; г - при отрыве дислокаций от точек закрепления, ε - скорость деформации, σ - напряжение, N - скорость счета АЭ-сигналов, активности АЭ с плотностью подвижных дислокаций, не получившие подтверждения в общем случае.
По-видимому, установленным можно считать соотношение между уровнем непрерывной АЭ и скоростью пластической деформации вида При неизменном механизме деформации в широком диапазоне скоростей деформации, согласно выводам, такая связь представляется естественной. Предложена более общая формула: σАЭ≈ε1/2εs, где -1,5≤s≤0,5.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.