Расчёты скважины № 87 ОАО НК «Роснефть-Пурнефтегаз». Расчёт насоса и клапана

4 РАСЧЁТНАЯ ЧАСТЬ

4.1 Расчёт насоса

4.1.1 Расчёт рабочих параметров насоса

Все расчёты будем вести для скважины № 87 ОАО НК «Роснефть-Пурнефтегаз»

Характеристика скважины №: 87 ОАО НК «Роснефть-Пурнефтегаз»:

диаметр эксплуатационной колонны…………………………………………146 мм

максимальная кривизна скважины 1000 м……………………………………2°
пластовое давление, Нст……………………………………………………….27,4 МПа буферное давление……………………………………………………………..11,1 МПа
глубина спуска насоса…………………………………………………………1206 м длина хода………………………………………………………………………2,5м число качаний в минуту……………………………………………………….2,5
дебит скважины:

 по жидкости,  ………………………………………………………………11м³/сут

по нефти (обводнённость 88 %), …………………………………………..3,6 т/сут

Подачей штангового насоса называется количество жидкости, подаваемое насосом в единицу времени.

Условная теоретическая подача (м³/сут.) насосной установки по длине хода устьевого штока выражается следующим образом [5, c.134]:

м³/сут.,                                    

где м² [5, c.134] – площадь сечения плунжера для насоса диаметром 44,5     мм,

S – длина хода устьевого штока, м;

n – число ходов в минуту.

Фактическая подача насоса всегда меньше теоретической, так как длина хода устьевого штока, измеренная на поверхности, вследствие упругих деформаций штанг и труб не соответствует истинной длине хода плунжера и, следовательно, теоретический геометрический объём, измеренный по длине хода устьевого штока, будет отличаться от объёма, описанного плунжером.

Кроме того, фактическая подача зависит от пригонки плунжера к цилиндру насоса, герметичности труб и клапанных узлов насоса, наличия газа, песка, воды и парафина в нефти, числа качаний, длины хода плунжера и других факторов. Поэтому фактическая подача жидкости на поверхности может быть значительно меньше объёма жидкости, поступающей в цилиндр насоса.

Фактическая подача:

м³/сут.,

где  - коэффициент подачи насоса [5, c.134].

Утечки в зазоре плунжерной пары нового (неизношенного) насоса рассчитывают по формуле А. М. Пирвердяна [5, c.146].

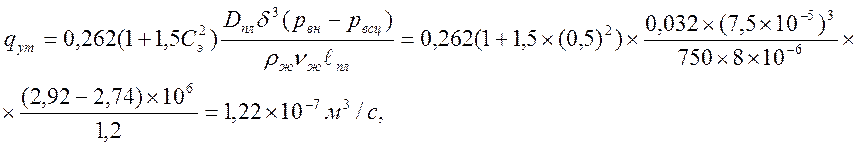
где   - соответственно плотность и кинематическая вязкость откачиваемой жидкости;

  - диаметр и длина плунжера, м (для серийных насосов  м);

 - зазор между плунжером и цилиндром при их концентричном расположении, м;

 - относительный эксцентриситет расположения плунжера в цилиндре, т. е. отношение расстояния между их центрами к величине  (); для практических расчётов  можно принять равным 0,5;

 - давление на выходе насоса;

 - давление всасывания в цилиндре.

4.1.2 Расчёт на прочность деталей насоса

Цилиндр насоса подвергается действию внутреннего давления, изменяющегося от нуля до максимального значения, под действием которого в теле насоса возникают тангенциальные и радиальные напряжения. Максимальные напряжения можно определить в зависимости от соотношения внутреннего  и наружного  радиусов цилиндра [4, c.118]:

при

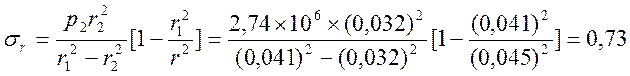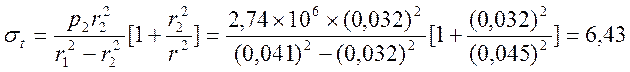 МПа

 МПа,

где  – внутреннее давление;

r – текущее значение радиуса [4, c.119].

Величину  определяют по третьей теории прочности

 МПа

 МПа [4, c.119].

 4.1.3 Расчёт параметров надёжности работы насоса

Таблица 4.1 – Статистическая информация о наработке до отказа штангового насоса с усовершенствованным клапаном в НГДУ «Аксаковнефть»  сут.

210	349	152	130	72	355	23	170	48	366
33	180	138	153	30	259	8	389	24	138
113	320	313	218	29	162	253	78	118	68
117	125	237	265	111	140	241	171	277	255

Число информации n=40.

Для облегчения расчётов при числе информации n>25 статистический материал обычно представляется в виде статистического ряда.

Число интервалов ряда примем равным:

Величину одного интервала определим по выражению:

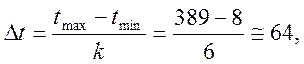
где – наибольшее значение статистического ряда;

– наименьшее значение статистического ряда;

– ширина интервала.

При составлении статистического ряда для каждого интервала подсчитывают:

– количество значений случайной величины в i-м интервале;

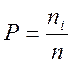– частность (опытная вероятность) в i-м интервале;

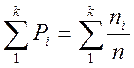– накопленная частность;

– эмпирическая плотность вероятности.

По данным таблицы 4.1 построен статистический ряд (таблица 4.2):

Таблица 4.2 – Статистический ряд

Интервал, сут.	Середина интервала , сут.	Частота	Опытная вероятность
0-64	32	7	0,175	0,175	0,0027
65-128	96	8	0,2	0,375	0,0031
129-192	160	10	0,25	0,625	0,0039
193-256	224	6	0,15	0,775	0,0023
257-320	288	5	0,125	0,9	0,0019
321-389	355	4	0,1	1	0,0015

Функция распределения случайной величины может быть достаточно строго определена с помощью статистических характеристик, называемых параметрами распределения.