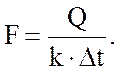
Средний логарифмический или арифметический температурный напор для прямотока и противотока определяется из формул
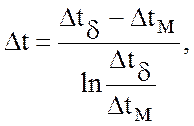 или (при
или (при 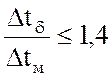 )
)
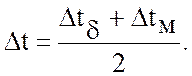 (2.4)
(2.4)
Величины температурных перепадов на концах аппарата Δtδ и Δtм обозначены на рис. 3.
Коэффициент теплопередачи
К рассчитывается по формуле для плоской стенки, что допустимо при 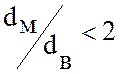
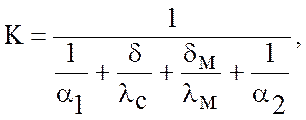 (2.5)
(2.5)
где α1 – коэффициент теплоотдачи от горячего теплоносителя к поверхности стенки, кВт/( м2∙K);
α2 – коэффициент теплоотдачи от поверхности стенки к холодному теплоносителю, кВт/( м2∙K);
δс – толщина стенки трубок, м;
λс – коэффициент теплопроводности материала стенки трубок, кВт/(м∙К);
dн, dв – соответственно наружный и внутренний диаметр трубок, м;
δнак, λнак – соответственно толщина, м и коэффициент теплопроводности слоя накипи или отложений, кВт/(м∙К).
Значения α1 и α2 рассчитываются по уравнениям подобия (см. подраздел 2.2).
При известной поверхности теплообменника F определяют другие геометрические характеристики теплообменного аппарата: длину трубчатого пучка L и число секций N.
2.2.2 Расчет коэффициента теплоотдачи
1) Теплоотдача при вынужденном течении теплоносителя по трубам и каналам
Уравнение подобия при вынужденном течении однофазного теплоносителя по трубам и каналам имеет вид:
при ламинарном вязкостно-гравитационном течении (Reж,d < 2300, Grж,d·Prж > 8·105)
![]() ; (2.6)
; (2.6)
при ламинарном вязкостном течении (Reж,d < 2300, Grж,d·Pr ж < 8·105)
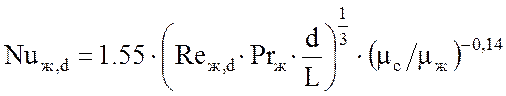 ; (2.7)
; (2.7)
при переходном течении (Reж,d = 2300…104)
![]() ; (2.8)
; (2.8)
при турбулентном течении (Reж,d > 104)
![]() ; (2.9)
; (2.9)
где ![]() – число Нуссельта;
– число Нуссельта;
![]() –
число Рейнольдса;
–
число Рейнольдса;
![]() –
число Грасгофа;
–
число Грасгофа;
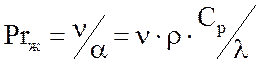 –
число Прандтля.
–
число Прандтля.
Индекс “ж” показывает,
что физические параметры теплоносителя, входящие в числа подобия, необходимо
принимать по средним температурам горячего теплоносителя t1 или холодного теплоносителя t2, для которых ![]() или
или ![]() .
.
Индекс “с” в числе
показывает, что физические параметры теплоносителя, входящие в число подобия,
необходимо брать по температуре стенки. В первом приближении можно принять ![]() .
.
В числа подобия введены обозначения: dэкв – эквивалентный диаметр, м; λ – коэффициент теплопроводности, кВт/(м·К); ν – коэффициент кинематической вязкости, м2/с; β – коэффициент объемного расширения, 1/К; α – коэффициент температуропроводности; w – скорость течения теплоносителя, м/с; Сp – средняя массовая изобарная теплоемкость, кДж/(кг·К); ρ – плотность, кг/м3; g = 9,81 м/с2; δt – температурный напор (разница температур теплоносителя и стенки); k0 – коэффициент, определяемый по величине числа Рейнольдса (табл. 4.3).
Для каналов любого сечения dэкв = 4f/u, где f – площадь поперечного сечения канала, u – смоченный периметр сечения. При движении теплоносителя в трубах круглого сечения определяющим линейным размером является внутренний диаметр трубы (dэкв = dв).
При течении теплоносителя в межтрубном пространстве вдоль пучка труб, расположенного в цилиндрическом канале-кожухе, эквивалентный диаметр равен
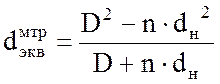 , (2.10)
, (2.10)
где D – внутренний диаметр кожуха теплообменника, м;
dн – наружный диаметр трубок, м.
После расчета численных
значений чисел подобия Grж,d, Reж,d, Prж, Prc определяют численное значение числа
Нуссельта по (2.6), (2.7), (2.8) или (2.9). Затем из соотношения ![]() находят коэффициент теплоотдачи
находят коэффициент теплоотдачи
![]() .
(2.11)
.
(2.11)
2) Теплоотдача при кипении жидкости
Коэффициент теплоотдачи αк при кипении жидкости в большом объеме может быть рассчитан по формулам
при 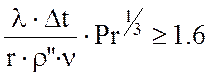
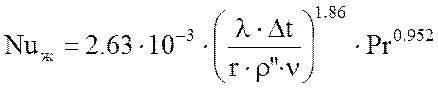 ; (2.12)
; (2.12)
при 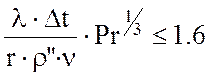
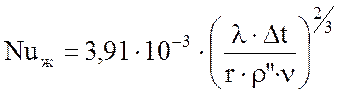 , (2.13)
, (2.13)
где ![]() –
коэффициент теплопроводности, теплота парообразования, кинематический
коэффициент вязкости жидкости и плотность пара при температуре насыщения ts; tc – температура поверхности стенки
трубы.
–
коэффициент теплопроводности, теплота парообразования, кинематический
коэффициент вязкости жидкости и плотность пара при температуре насыщения ts; tc – температура поверхности стенки
трубы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.