







Задания самостоятельной работы
для студентов специальности 080507.65 – Менеджмент организации,
всех форм обучения
по дисциплине «Математика»
В партии из n=14 изделий k=5 изделий бракованные. Какова вероятность того, что взятые случайным образом m=3 изделий будут бракованными?
А1 – событие, состоящее в том, что первое взятое изделие бракованное;
А2 – событие, состоящее в том, что второе взятое изделие бракованное;
Событие, состоящее в том, что взятые три изделия бракованные есть произведение событий А1 А2 А3.
P(A1A2A3) = P(A1)P(A2/A1)P(A3/A1A2).
Вероятность события А1
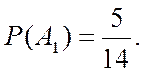
Условная вероятность P(A2/A1)события А2 при условии, что событие А1 произошло
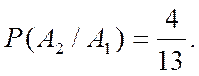
Условная вероятность P(A3/A1A2)события А3 при условии, что события А1 и А2 произошли
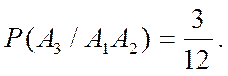
Окончательно получаем
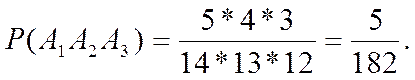
Ответ: 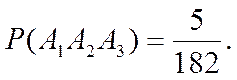
Непрерывная случайная величина X, имеющая математическое ожидание Mx=24 и среднее квадратическое отклонение sx=1, распределена по нормальному закону. Найти вероятность того, что в результате испытания случайная величина примет значение из интервала (a, b)=(20, 26) .
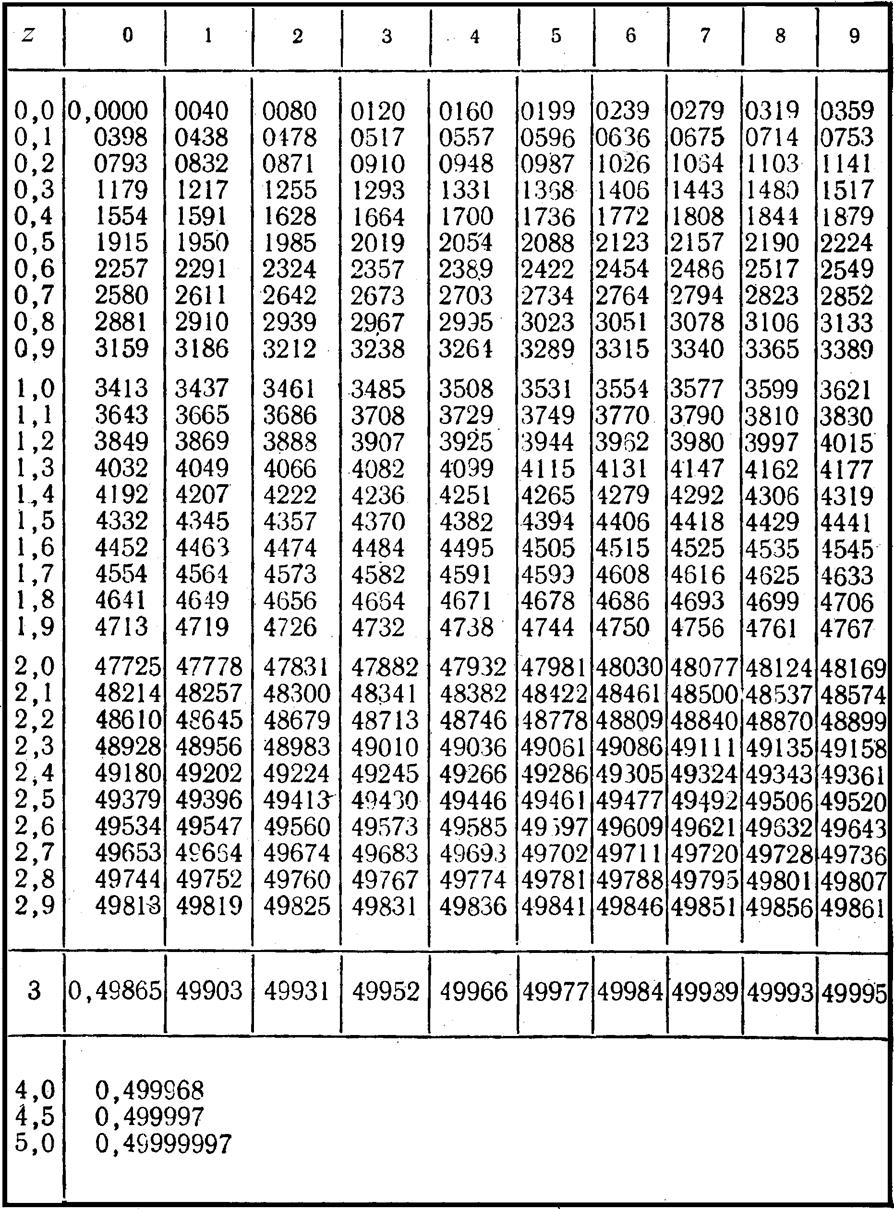
Указание: использовать таблицу значений нормированной функции Лапласа
– приложение 1.
Из свойства функции распределения, вероятность попадания нормально распределенной случайной величины Х в заданный интервал х1 < X < x2 может быть выражена в виде разности значений функции распределения в граничных точках интервала:
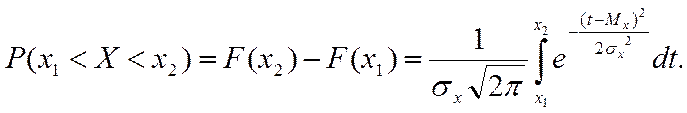
Если воспользоваться интегралом
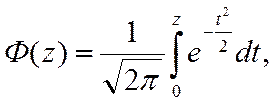
который называется функцией Лапласа, то искомая вероятность через функцию Лапласа запишется в виде
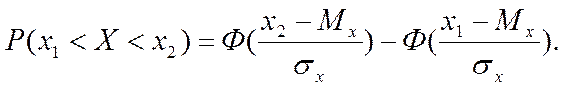
Или в обозначениях нашей задачи
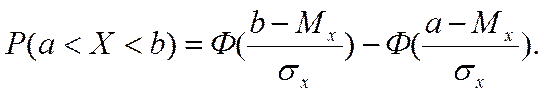
Функцию Лапласа нельзя выразить через элементарные функции, поэтому определяют их численные значения, которые помещают в специальные таблицы (см. приложение 1).
Поэтому, сначала вычисляем аргументы функции Лапласа
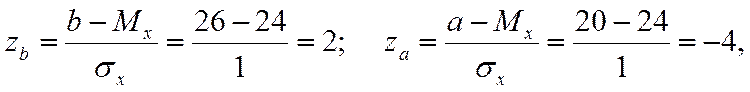
а затем, используя таблицу приложения 1 для вычисления функции Лапласа, находим искомую вероятность. Учитывая, что функции Лапласа является нечетной, т.е. Ф(–z)= – Ф(z) получаем
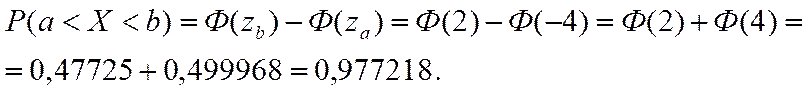
Ответ: Р(a< X< b) = Р(20 < X< 26) =0,977218.
Найти несмещенную (исправленную) выборочную дисперсию на основании данного распределения выборки.
|
xi |
2 |
7 |
9 |
10 |
|
ni |
8 |
14 |
10 |
18 |
Для вычисления дисперсии воспользуемся формулой
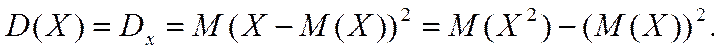
Выборочную дисперсию тогда можно вычислить на основе выборочного среднего так
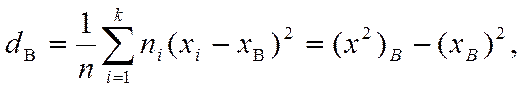
Имеем n = n1+ n2+ n3+ n4 = 8+14+10+18 = 50,
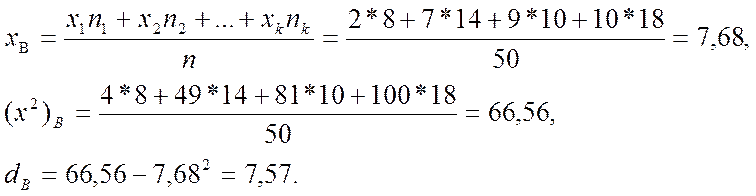
Находим несмещенную (исправленную) оценку дисперсии
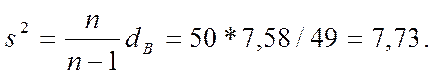
Ответ: s2=7,73.
Страховая компания выпустила четыре вида страховых полисов в предположении, что спрос на них будет одинаков. Фактические объемы реализации полисов приведены в таблице.
Оценить для уровня значимости a = 0,01 согласуется ли фактическая реализация теоретическому предположению о равномерности спроса на все виды страховых полисов?
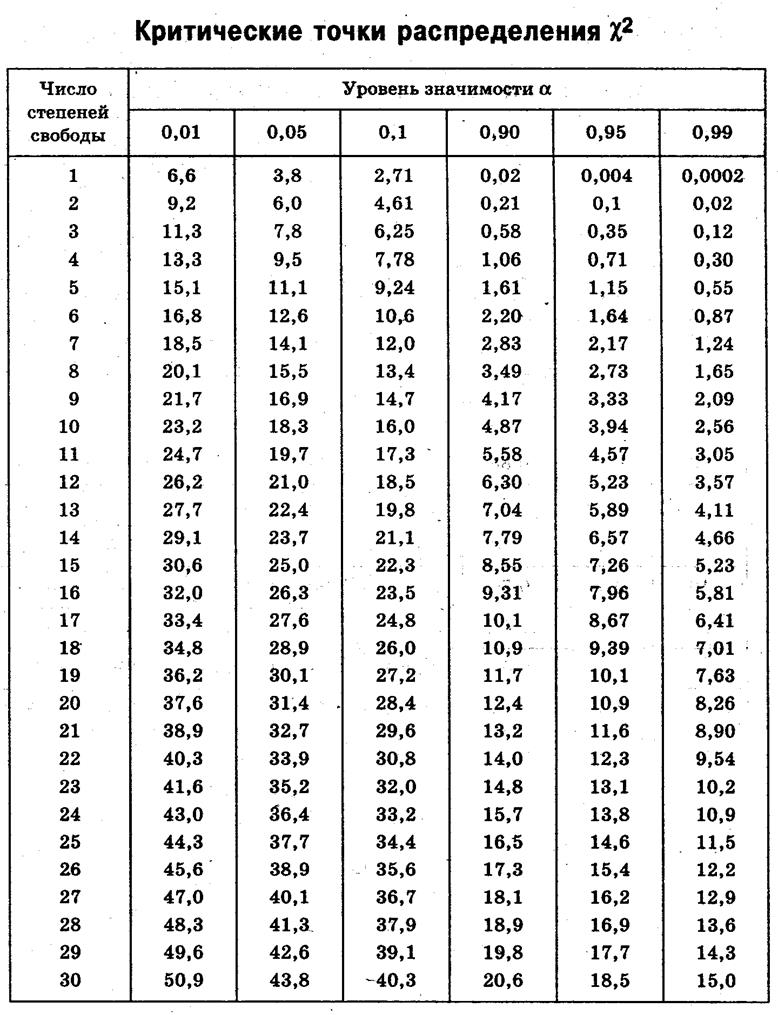
Указание: использовать таблицу – приложения 2.
|
№ полиса |
1 |
2 |
3 |
4 |
|
Объем реализации |
50 |
21 |
23 |
26 |
Проверяем нулевую гипотезу о равномерности спроса на все виды страховых полисов, т.е. полагаем полагаем теоретические объемы продаж m1Т, m2Т, m3Т и m4Т равными
m1Т= m2Т= m3Т=m4Т=( m1+ m2+ m3 + m4)/4=(50+21+23+26)/4=30.
Составим таблицу
|
№ полиса |
i |
1 |
2 |
3 |
4 |
|
Фактический объем реализации |
mi |
50 |
21 |
23 |
26 |
|
Ожидаемый объем реализации |
miT |
30 |
30 |
30 |
30 |
Рассчитаем значение критерия согласия Пирсона
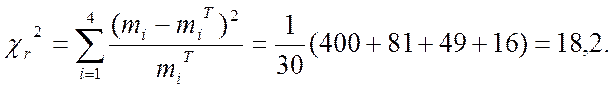
Для уровня значимости a = 0,01 по таблице c2 - распределения для числа степеней свободы L = 4 – 1 =3 (L = n – r – 1) находим c2кр = 11,3.
Т.к. для уровня значимости a = 0,01 критическая область представляет собой интервал (c2кр; ¥ ) = ( 11,3; ¥ ), а cr2=18,2 принадлежит критической области, то нулевая гипотеза о равномерности спроса на все виды страховых полисов отвергается.
Ответ: нулевая гипотеза о равномерности спроса отвергается.
На основании измерений величин X и Y найти выборочное уравнение линейной регрессии Y на X и выборочный коэффициент корреляции.
|
X |
xi |
3 |
5 |
7 |
9 |
10 |
|
Y |
yi |
14 |
10 |
9 |
8 |
6 |
Решение
Будем искать линейное выборочное уравнение регрессии Y на X в виде
M(Y / X=x) = j(x) = aх + b.
Оценки aи bпараметров будем находить по методу наименьших квадратов, как минимизацию суммы квадратов уклонения линии уравнения регрессии, вычисленных в точках xi, от опытных данных yi, т.е.
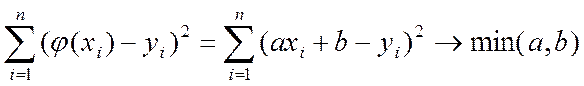
Оценки aи b, обеспечивающие решение этой задачи, имеют вид
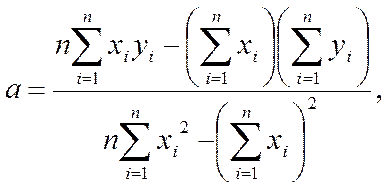
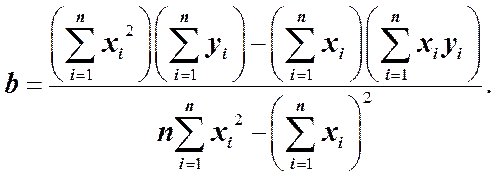
Составим расчетную таблицу
|
x |
y |
x2 |
xy |
y2 |
|
|
3 |
14 |
9 |
42 |
196 |
|
|
5 |
10 |
25 |
50 |
100 |
|
|
7 |
9 |
49 |
63 |
81 |
|
|
9 |
8 |
81 |
72 |
64 |
|
|
10 |
6 |
100 |
60 |
36 |
|
|
å |
34 |
47 |
264 |
287 |
477 |
Определяем
a =(5*287–34*47)/(5*264-342)= – 0,99,
b = (264*47– 34*287)/(5*264 – 342) = 16,16.
Выборочный коэффициент корреляции имеет вид
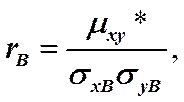
где выборочные средние квадратические отклонения вычисляются как:
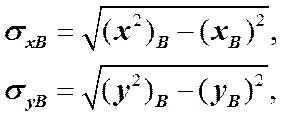
а выборочный эмпирический корреляционный момент
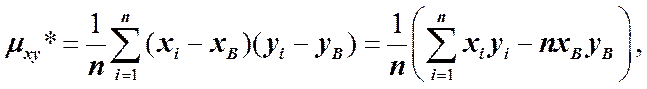
где xB и yB - выборочные средние:
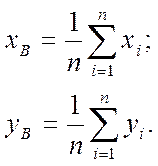
В результате имеем
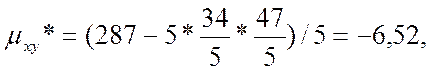
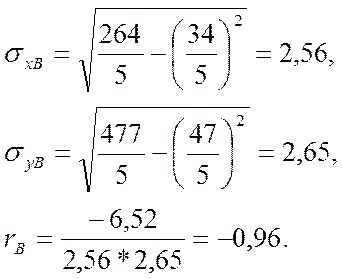
Ответ: j(x) = –0,99х + 16,16; rB = –0,96.
Приложение 1
Нормированная функция
Лапласа 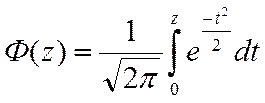
Приложение 2
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.