



Министерство Образования и Науки РФ
Российский государственный социальный университет
Филиал в г . Красноярске
Вариант № 2
Выполнила студентка гр. Ф-З-3-09
Специальность «Финансы и кредит»:
Кузнецова Анастасия Андреевна
Зачетная книжка №13812
Проверил научный руководитель: Чайка С.Н.
Красноярск 2011
Задание 1
Банком выдана ссуда в размере 1000 руб, при условии, что через год заемщик возвратит банку сумму в размере 1250 руб.
Оценить доходность этой сделки для банка величинами процентной (r) и учетной (d) ставок.
Решение:
PV=1000(современная стоимость)
FV=1250(будущая стоимость)
r= (FV-PV)/PV= (1250-1000)/1000=0,25
d= (FV-PV)/FV= (1250-1000)/1250=0,2
Ответ: r=0,25; d=0,2.
Задание 2:
в конце сделки клиент получит сумму FV согласно формулы переменной ставки r1, r2, …, rm действующей на последовательных интервалах начисления процентов n1, n2, …, nm
Клиент внес вклад в банк в сумме 100 тыс. руб. под простую процентную ставку в 20 % годовых сроком на 2,5 года. В начале каждого последующего года банк уменьшал процентную ставку на 1,5 % годовых.
Какую сумму клиент получил в конце сделки?
Каков коэффициент наращения за все время сделки?
Решение:
FV=PV*(1 +![]() nk*rk) = PV*kn
nk*rk) = PV*kn
При этом коэффициент наращения kn за все время сделки
kn =(1 +![]() nk*rk)(коэффициент наращения),
nk*rk)(коэффициент наращения),
где m – число интервалов начисления процентов.
По условиям задания
m = 3
за первый год n=1,r=1*0,2=0,2;
За второй год:n=1,r=0,185;
За последний период:n=0,5,r=0,17
kn =(1 + n1*r1 + n2*r2 + n3*r3 )=(1 + 0,2+ 1*0,185 + 0,5*0,17)=1,47
FV=PV*kn =100000*1,47 = 147000
Ответ: FV=147000 руб.; kn = 1,47
Задание 3
В банк положен депозит под 6,2 % годовых в размере 10 тыс. долларов со сроком погашения через 2 года. Проценты начисляются каждые полгода с присоединением к накопленной сумме.
Определить сумму, которую получит вкладчик по истечении срока депозита.
Определить величину эффективной полугодовой ставки.
Решение:
PV=10000
r=0,062
n=2 – длительность сделки в годах
m=2 – внутригодовая частота начисления сложных процентов
FV = PV*(1+r/ m)m*n = 10000*(1 + 0,062/2)4 =10000*1,129886 = 11298,86
Величина эффективной полугодовой ставки:
reff (EPR) = (1 + r/ m)m - 1 = (1 + 0,062 / 2)2 - 1 = 0,063
Ответ: FV=11299 долларов; reff (EPR) = 0,063
Задание 4
Вы решили через 2 года приобрести автомобиль стоимостью 200000 руб.
С этой целью Вы намерены сегодня воспользоваться услугами банка, предоставляющего ссуду под 10,6 % годовых с ежегодной капитализацией процентов.
Какая сумма должна быть положена в банк?
Чему равен коэффициент дисконтирования?
Решение:
Из формулы начисления сложных процентов предыдущего задания следует:
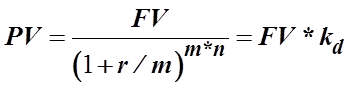
где kd – коэффициент дисконтирования (приведения)
|
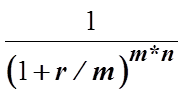
По условиям задания
FV = 200000
n = 2
m = 1
r = 0,106
Тогда
PV = 200000/(1+0.106/1)2 = 244647.2
kd = 1/(1+0.106/1)2 = 0,8175
Ответ: PV=244647.2 руб. ; kd = 0,8175.
Задание 5:
На счет сына в банке, со дня его рождения, отец в конце каждого квартала начинает вносить суммы в размере 1950 руб., на которые банком будут начисляться с ежеквартальной капитализацией проценты по ставке 8% годовых.
Определить сумму, которую банк выплатит сыну в день его совершеннолетия.
Решение:
Воспользуемся формулой:
FVn=CF*(1+r)n-1+
CF*(1+r)n-2+…+
CF = 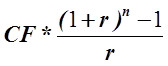
накопленной суммы за n лет при годовой капитализации процентов по ставке r % годовых при условии, что вклады в размере CF руб. вносились в конце каждого года. Преобразуем формулу согласно условий нашей задачи.
Если m количество взносов и начислений в течение года, то общее число платежей за n-лет будет равно m*n, а процентная ставка периода начисления равна r/m. Тогда получим:
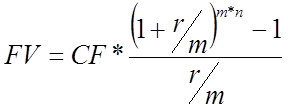
В условиях нашего задания:
CF = 1950
m* n = 4*18 = 72
r/m= 0,08/4 = 0,02
FV = 1950*( 1,0272 - 1)/0,02 = 308210,5
Ответ: FV=308210,5 руб.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.