Задача 1
Предприятие получило кредит в размере 22 млн. руб. сроком на 1 год с условием возврата 35 млн. руб. Определить сложную и простую процентные ставки.
Решение:
1. Рассмотрим нахождение простой процентной ставки, для этого необходимо воспользоваться формулой для нахождения наращенной суммы с использованием простых процентов, а из неё выразить величину процентной ставки:
![]()
Выразим процентную ставку:
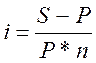
Подставим исходные данные и получим:
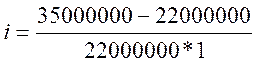
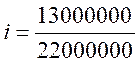
![]()
2. Рассмотрим нахождение сложной процентной ставки, для этого необходимо воспользоваться формулой для нахождения наращенной суммы с использование сложных процентов, но нам известно, что срок составляет 1 год. Таким образом, формула примет следующий вид:
![]()
Выразим процентную ставку:
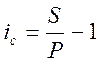
Подставим исходные данные и получим:
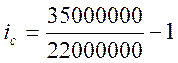
![]()
![]()
Ответ: Процентные ставки, найденные с использованием формул нахождения простых и сложных процентов, составили 59 %.
Задача 2
Найти возвращаемую сумму, если взятая ссуда составляет 280 тыс. руб., а срок её погашения равен 1,6 лет. Контрактом предусмотрена сложная процентная ставка в размере 15 % годовых. Начисление процентов производится ежеквартально.
Решение:
Для решения данной задачи воспользуемся формулой начисления процентов за периоды менее 1 года:
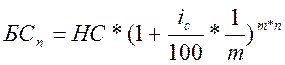
где БС – будущая стоимость;
НС – настоящая стоимость;
iс – процентная ставка;
m – количество периодов начисления;
n – срок начисления.
Подставим в данную формулу исходные данные:
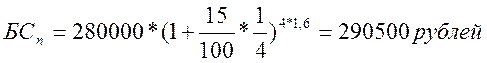
Ответ: Наращенная сумма в конце срока вклада составила 290500 рублей.
Задача 3
Проведите анализ двух вариантов накопления средств по схеме аннуитета постнумерандо:
Вариант 1. Каждые полгода вносится вклад по 20 тыс. руб. При условии, что банк начисляет 12 % годовых с полугодовым начислением сложных процентов;
Вариант 2. Делается ежегодный вклад в размере 42 руб. при начислении 15% годовых ежегодно.
Требуется определить величины накопленной суммы через 10 лет в каждом варианте. Какой из этих вариантов более предпочтителен? Изменится ли Ваше предпочтение, если процентная ставка в варианте 2 изменится до 13 %?
Решение:
Для расчёта задачи воспользуемся формулой для расчёта аннуитета постнумерандо:
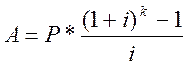
где к – количество начислений за весь срок.
Подставим в данную формулу исходные данные:
а) начисление каждые полгода (сложные проценты):
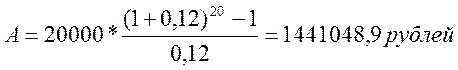
б) начисление ежегодное:
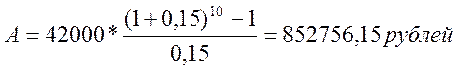
В) начисление ежегодное, со сменой ставки с 15% до 13%
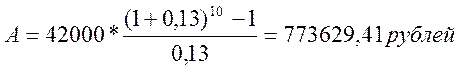
Ответ: Более прибыльный результат 1 – начисление процентов каждые полгода.
Задача 4
Клиент планирует разместить в банке 120 тыс. руб. Сроком на два года под 30 % годовых. Прогноз темпа роста инфляции составляет 20 % в год. Определить реальную сумму денег, которую клиент сможет иметь через два года и реальную годовую ставку процента.
Решение:
Для определения стоимости будущей суммы денег на настоящий момент времени с учётом инфляционного обесценения используем формулу:
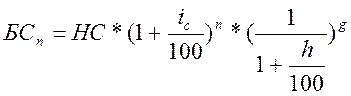
где h – уровень инфляции
Подставим исходные данные и получим:
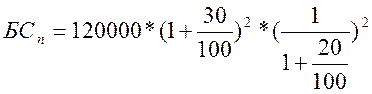
БС = 140 833,3 рублей
Определим эффективную ставку процентов, для этого доход от операции необходимо разделить на величину вклада и умножить на 100 %:
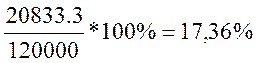
Ответ: Реальная ставка процента составила 17,36 %, доход клиента от вложенных 120 000 рублей составит 20 833,3 рублей.
Задача 5
С помощью оценок эффективного годового процента сравните два варианта начисления процентов:
Вариант 1. Начисления производятся каждые полгода при годовой процентной ставке 16 %.
Вариант2. Начисления производятся ежемесячно при годовой процентной ставке 14 %.
Определить какой из этих вариантов более предпочтительным при размещении вклада на 4 года.
Решение:
Проведем сравнительный анализ оценок эффективного процента:
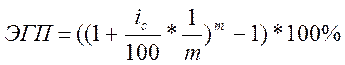
а) для 16%, каждые полгода:
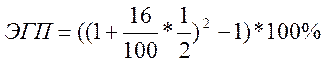
ЭГП = 16,64%
б) для 14 %, ежемесячно:
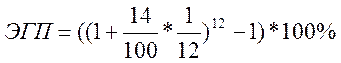
ЭГП = 14,93 %
Для того чтобы сделать вывод о том, какой из банков (вариантов) предпочтительнее, необходимо рассчитать доход который получит владелец от вклада в размере 10 000 000 рублей:
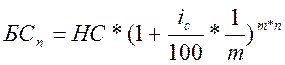
Для варианта 1:
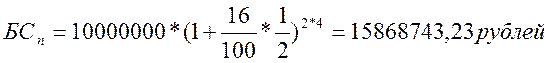
Для 2 варианта:
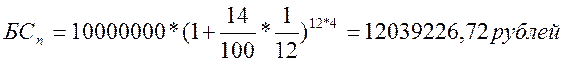
Ответ: вкладчик выберет первый банк, так как его доход от вложенных 10 000 000 рублей больше, чем во втором банке.
Задача 6
Фирма заключила сделку с банком о предоставлении ей ссуды в сумме 15 млн. руб. сроком на два года на следующих условиях: за первый год плата за ссуду будет начисляться исходя из 20 % годовых по простой ставке, в каждом последующем полугодии процент будет возрастать на 5 %. Какова будет возвращаемая сумма долга?
Решение:
Для решения данной задачи воспользуемся формулой для нахождения наращенной суммы по формуле простых процентов. Но для начала рассчитаем проценты:
1 год = 20 %;
0,5 год. = 20 %+5 % = 25 %;
0,5 года = 25% + 5 % = 30 %
![]()
S = 15 000 000 * (1+0,2*1+0,25*0,5+0,3*0,5) = 22 125 000 рублей
Ответ: Фирме заключившей данный контракт необходимо будет вернуть банку сумму денег в размере 22 125 000 рублей.
Задача 7
Фирма заключила сделку с банком о предоставлении ей ссуды в сумме 15 млн. руб. сроком на два года на следующих условиях: в первом полугодии – из расчета 30 % годовых по простой ставке, во втором полугодии ставка возрастает на среднюю полугодовую индексную надбавку; на втором году ставка будет расти на 10 % каждый квартал. При этом известно, что с учётом инфляции индексная надбавка в третьем квартале первого года составила 46 %, в четвёртом квартале – 54 %.какова будет возвращаемая банку сумма денег в этих условиях? Определить доход банка.
Решение:
Для решения данной задачи воспользуемся формулой для нахождения наращенной суммы по формуле простых процентов. Но для начала рассчитаем проценты:
0,5 года = 30 %;
0,5 года = (46+54)/2+30 % = 80 %
1 квартал = 80 %+ 10 % = 90 %;
2 квартал = 90 % + 10 % = 100 %;
3 квартал = 100 % + 10 % = 110 %;
4 квартал = 110 % + 10 % = 120 %.
![]()
S = 15 000 000 * (1 + 0,5*0,3 + 0,5*0,8 + 0,25*0,9 + 0,25*1 + 0,25*1,1 + 0,25*1,2) = 39 000 000 рублей
Ответ: Доход банка составит 24 000 000 рублей.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.