Определение коэффициента годности и восстановления деталей.
Сводную ведомость информации по износам представим в виде таблицы 1; в которой полученные расчетом износы расположены в порядке их возрастания.
Таблица 1
Информация 26. Радиальный зазор подшипника 304 оси промежуточной шестерни муфты сцепления трактора МТЗ-50
|
№ n/n |
Износ, мм. |
№ n/n |
Износ, мм. |
№ n/n |
Износ, мм. |
№ n/n |
Износ, мм. |
№ n/n |
Износ, мм. |
|
1 |
0,06 |
7 |
0,14 |
13 |
0,20 |
19 |
0,26 |
25 |
0,33 |
|
2 |
0,08 |
8 |
0,15 |
14 |
0,20 |
20 |
0,27 |
26 |
0,34 |
|
3 |
0,10 |
9 |
0,16 |
15 |
0,21 |
21 |
0,28 |
27 |
0,35 |
|
4 |
0,11 |
10 |
0,17 |
16 |
0,22 |
22 |
0,28 |
28 |
0,36 |
|
5 |
0,12 |
11 |
018 |
17 |
0,23 |
23 |
0,29 |
29 |
0,39 |
|
6 |
0,13 |
12 |
0,19 |
18 |
0,25 |
24 |
0,32 |
30 |
0,45 |
Допустимый размер – 0,15мм.
Статистический ряд информации составляем в виде таблицы (табл. 2), состоящей из пяти строк: интервалы, середины интервалов, частота, опытная вероятность и накопленная опытная вероятность.
Всю информацию по износам разбиваем на интервалы, количество которых определяется по формуле:
![]() ,
,
где N – количество информации (количество измеренных деталей)
![]()
Протяженность одного интервала.
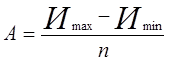 ,
,
где Иmax и Иmin - соответственно наибольшее и наименьшее значения износов (табл. 2)
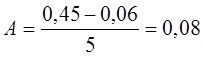
Протяженность интервала всегда округляют в большую сторону. Интервалы должны быть одинаковыми по величине и прилегать друг к другу без разрывов. Начало первого интервала или начало рассеивания (сдвиг износов) определяется по формуле:
![]() ,
,
где И1 – значение износа в первой точке информации, мм.
![]()
Принимаем С=0,02. При распределении износов чаще всего С=0, то есть нет сдвига рассеивания.
Число интервалов и их протяженность используются для построения первой строки статистического ряда. Вторая строка этого ряда представляет собой середину каждого интервала. Например, для первого интервала:
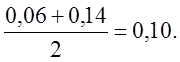
Третья строка показывает частоту, то есть сколько деталей попадает в каждый интервал износов (берут из табл.1). Например в первом интервале (0,06 – 0,14мм) частота m1=7; во втором - m2=9; в третьем m3=7 и т.д.
Значения опытных вероятностей в каждом интервале (четвертая строка статистического ряда) определяется по формуле:
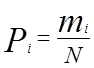 ,
,
где mi – опытная частота в i-ом интервале.
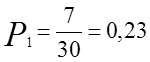 ;
; 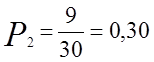
Значения накопленных опытных вероятностей (последняя строка ряда) определяют суммированием вероятностей по интервалам:
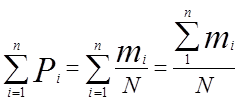 ,
,
![]() =0,23;
=0,23; ![]() =0,23+0,30=0,53;
=0,23+0,30=0,53; ![]() =0,53+0,23 =0,76 и т.д.
=0,53+0,23 =0,76 и т.д.
Сумма частот ![]() по всем
интервалам должна быть равна N=30, а сумма накопленных
опытных вероятностей
по всем
интервалам должна быть равна N=30, а сумма накопленных
опытных вероятностей ![]()
Таблица 2
Статистический ряд
|
Интервал, мм |
0,06-0,14 |
0,14-0,22 |
0,22-0,30 |
0,30-0,38 |
0,38-0,46 |
|
Середина интервала, Исрi |
0,10 |
0,18 |
0,26 |
0,34 |
0,42 |
|
Частота |
7 |
9 |
7 |
5 |
2 |
|
Опытная вероятность, Рi |
0,23 |
0,30 |
0,23 |
0,17 |
0,07 |
|
Накопленная опытная
вероятность, |
0,23 |
0,53 |
0,76 |
0,93 |
1 |
Определение числовых характеристик. Основными числовыми характеристиками распределения случайной величины являются среднее значение, среднее квадратичное отклонение и коэффициент вариации.
Среднее квадратическое отклонение
представляет собой абсолютную меру, а коэффициент вариации – относительную
меру рассеивания случайной величины. При объеме информации N![]() 25 их определяют следующим
образом.
25 их определяют следующим
образом.
Среднее значение износа
![]()
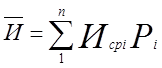 ,
,
![]() где Исрi – значение износа в середине i-го
интервала ;
где Исрi – значение износа в середине i-го
интервала ;
![]() Рi - опытная вероятность в i-ом
интервале.
Рi - опытная вероятность в i-ом
интервале. ![]()
![]() =0,10×0,23+0,18×0,30+0,26×0,23+0,34×0,17+0,42×0,07=0,224»0,22
мм.
=0,10×0,23+0,18×0,30+0,26×0,23+0,34×0,17+0,42×0,07=0,224»0,22
мм.
Среднее квадратическое отклонение:
![]()
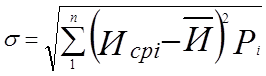 ,
,
![]()
![]() мм.
мм.
Коэффициент вариациии:
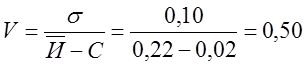
Проверку информации на наличие выпадающих точек осуществляют по формуле:
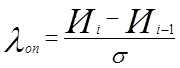 ,
,
где Иi и Иi-1 – смежные точки в сводной ведомости информации (табл.1).
Для наименьшего значения износа И2=0,10; И1=0,06.
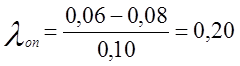
Для наибольшего значения износа И30=0,45; И29=0,39.
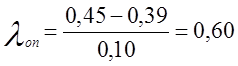
Полученные значения lоп сравнивают с табличными значениями критерия Ирвина. Если lоп < lт информация достоверна, если же lоп > lт ,то такие точки «выпадают», то есть должны быть исключены из информации как недостоверные.
В нашем случае при N=30 и доверительной вероятности a =0,95 табличное значение критерия Ирвина lт=1,2 то есть больше lоп. Поэтому с вероятностью 0,95 можно утверждать, что все точки информации достоверны.
Графическое построение опытного распределения износов.
Построение гистограммы осуществляется следующим образом (рис 1).
По оси абсцисс откладывают интервалы в соответствии со статистическим рядом, а по оси ординат - опытную вероятность Р в начале и конце каждого интервала. Соединив построенные в каждом интервале точки получаем прямоугольник. В результате получается ступенчатый многоугольник – гистограмма . Площадь каждого прямоугольника в процентах от общей площади гистограммы или долях единицы определяет опытную вероятность или количество деталей, у которых износ находится в данном интервале. Построение полигона (рис. 1) осуществляется по точкам, образованным пересечением абсциссы, равной середине интервала, и ординаты, равной вероятности интервала, то есть надо соединить прямыми линиями середины верхних (горизонтальных) сторон прямоугольников гистограммы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.