Фильтрация бинарных изображений. Медиана. Ранговая фильтрация. Нормализация фона, страница 3

Процентильные фильтры обозначаются .

Легко заметить, что медианный фильтр есть частный случай процентильного  при .

В свете приведенных выше рассуждений, ясно, что фильтрацию с более «низкими» рангами, чем медиана следует применять в том случае, если вероятность перехода 1®0 существенно больше вероятности перехода 0®1. С более «высокими» рангами следует работать в том случае, если вероятность перехода 0®1 существенно больше вероятности перехода 1®0. Предельным случаем такого «асимметричного» шума является униполярный шум c параметрами (p = 1) или (q = 1). В этих случаях случае оптимальная ранговая фильтрация принимает вид максимального или минимального фильтра соответственно.

5) Расширение-сжатие (простая морфология)

Расширением называется итеративно применяемый к бинарному изображению максимальный фильтр с квадратной апертурой размера 3´3 пикселя. Соответственно сжатием называется итеративно применяемый минимальный фильтр с той же апертурой 3´3. Параметром, определяющим свойства фильтрации, при этом считается количество циклов сжатия и расширения.

Фильтрация типа расширение-сжатие может применяться для удаления слабого шума типа соль-перец, однако в этом качестве она уступает медианной фильтрации. Однако основная область применения таких фильтров – удаление сложных неслучайных искажений формы фигур. Не даром изначально такой прием фильтрации был предложен для выявления дефектов типа «разрывов» и «перемычек» металлических дорожек на изображениях печатных плат в задачах технического и технологического контроля.

Рассмотрим геометрический смысл операций расширения и сжатия на примере обработки искусственного изображения (рис. 3.2.31), на котором представлен прямоугольный объект, имеющий «дефекты формы» типа внутренних «дырок» и внешних «выступов». Попробуем средствами расширения-сжатия удалить эти дефекты формы объекта.

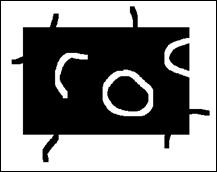
@Рис. 3.2.31. Изображение с «дефектами» типа «дырок» и «выступов»

Начнем с удаления внешних «выступов» формы. Для этого используется последовательность операций расширение-сжатие. На первом этапе этой процедуры выполняется операция расширения светлого фона (т.е. сжатия темного объекта) с таким числом циклов, которое полностью удаляет («съедает») внешние «выступы» формы. Однако внешний размер объекта при этом уменьшается, а внутренние дефекты, напротив, увеличиваются в размерах, в связи с чем после этого необходимо выполнить сжатие фона (т.е. расширение объекта) с тем же числом циклов. В результате выполнения обоих этапов операции расширения-сжатия внешние размеры и форма объекта оказываются полностью восстановлены, но внутренние дефекты формы сохраняются (рис. 3.2.32, 3.2.33).

@Рис. 3.2.32. Результат сжатия                      @Рис. 3.2.33. Результат расширения после

объекта                                                                   сжатия объекта             (удаление внешних

                                                                                  «выступов» формы)

Рассмотрим теперь аналогичную технику удаления внутренних дефектов формы («дырок»). Для этого используется обратный порядок операций: сжатие-расширение. На первом этапе этой процедуры выполняется операция сжатия фона (т.е. расширения объекта)  необходимым числом циклов, которое удаляет («заращивает») внутренние «дыры» и «каналы». Однако внешний размер объекта при этом увеличивается, внешние дефекты, также увеличиваются в размерах, в связи с чем после этого необходимо выполнить расширение фона (сжатие объекта) с тем же числом циклов. В результате выполнения всей операции сжатия-расширения в целом размеры и внутренняя целостность объекта оказываются восстановлены, но внешние дефекты формы сохраняются (рис. 3.2.34, 3.2.35).