1 ПРОЕКТУВАННЯ ПРИСТРОЮ НА ЛОГІЧНИХ ЕЛЕМЕНТАХ
1.1 Досконалі форми, таблиця відповідності
Спрощуємо задану функцію:
![]()
![]()
Побудуємо карти Карно за допомогою інверсної функції, замінивши нулі одиницями, а одиниці – нулями:
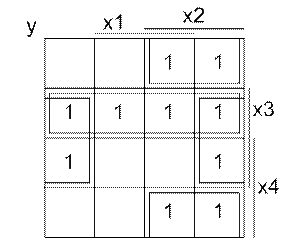
Рисунок 1.1 – Карта Карно для одиниць
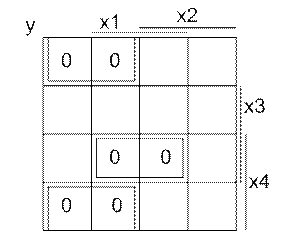
Рисунок 1.2 – Карта Карно для нулів
Зчитаємо ДКНФ, що складається з 6 макстермів, з рис. 1.2:
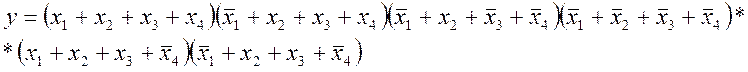
За допомогою приведеної ДКНФ побудуємо таблицю відповідності:
Таблиця 1.1 – Таблиця відповідності
|
x4 |
x3 |
x2 |
x1 |
y |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
|
2 |
0 |
0 |
1 |
0 |
1 |
|
3 |
0 |
0 |
1 |
1 |
1 |
|
4 |
0 |
1 |
0 |
0 |
1 |
|
5 |
0 |
1 |
0 |
1 |
1 |
|
6 |
0 |
1 |
1 |
0 |
1 |
|
7 |
0 |
1 |
1 |
1 |
1 |
|
8 |
1 |
0 |
0 |
0 |
0 |
|
9 |
1 |
0 |
0 |
1 |
0 |
|
10 |
1 |
0 |
1 |
0 |
1 |
|
11 |
1 |
0 |
1 |
1 |
1 |
|
12 |
1 |
1 |
0 |
0 |
1 |
|
13 |
1 |
1 |
0 |
1 |
0 |
|
14 |
1 |
1 |
1 |
0 |
1 |
|
15 |
1 |
1 |
1 |
1 |
0 |
1.2 Мінімізація функції, реалізація в базисах І-НЕ, АБО-НЕ, І-АБО-НЕ
Зчитуємо з рис. 1.1, 1.2 мінімізовані форми:
МДНФ:
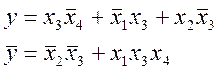
МКНФ:
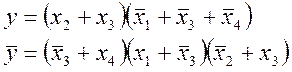
Запишемо вирази для реалізацій в базисах:
І-НЕ:
![]() , складність q = 7/12
, складність q = 7/12
АБО-НЕ:
![]() , складність q = 6/10
, складність q = 6/10
І-АБО-НЕ:
![]() , складність q = 5/9
, складність q = 5/9
Приведемо схеми в цих базисах:
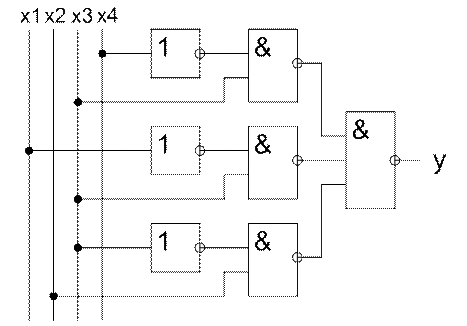
Рисунок 1.3 – Реалізація в базисі І-НЕ
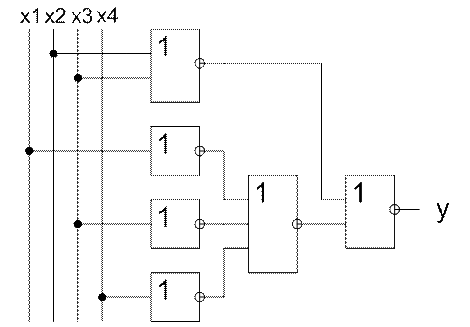
Рисунок 1.4 – Реалізація в базисі
АБО-НЕ
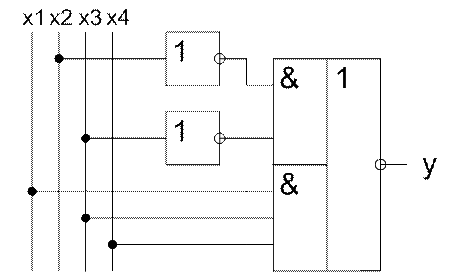
Рисунок 1.5 – Реалізація в базисі І-АБО-НЕ
1.3 Мінімізація схеми в базисі І-НЕ
Довизначимо функцію рис. 1.1 ще двома одиницями:
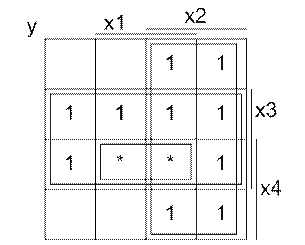
Рисунок 1.6 – Карта Карно для редукції
Проведемо редукцію:
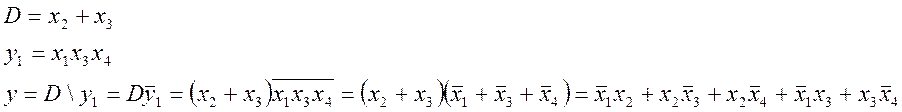
Очевидно, що редукція не призводить до простіших форм. Складність до редукції рівна складності після редукції.
1.4 Елементи технічного проектування пристрою
Для технічного проектування оберемо схему рис 1.5, так як в неї найменша складність. Проектування проведемо на мікросхемах К555ЛР11 та К555ЛН1.
Їхні параметри подані нижче в табл. 1.2
Таблиця 1.2 – Параметри мікросхем
|
Тип |
Uж, В |
Iсп, мА |
І10, мА |
І11, мА |
І21, мА |
U20, В |
U21, В |
tзт, нс |
|
К555ЛР11 |
5 |
2,8 |
0,36 |
0,02 |
0,1 |
0,5 |
2,7 |
20 |
|
К555ЛН1 |
5 |
6,6 |
0,36 |
0,02 |
0,1 |
0,5 |
2,7 |
20 |
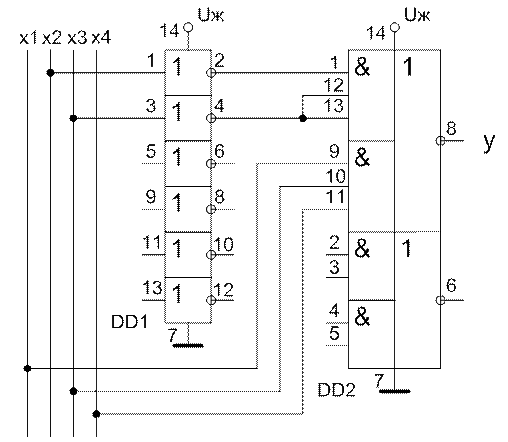
Рисунок 1.7 – Спроектована схема
DD1 – К555ЛН1, DD2 – К555ЛР11
1.5 Автоматичне проектування пристрою в графічному редакторі MAX+Plus II
Побудуємо в графічному редакторі схеми реалізацій в базисах І-НЕ, АБО-НЕ та І-АБО-НЕ відповідно:
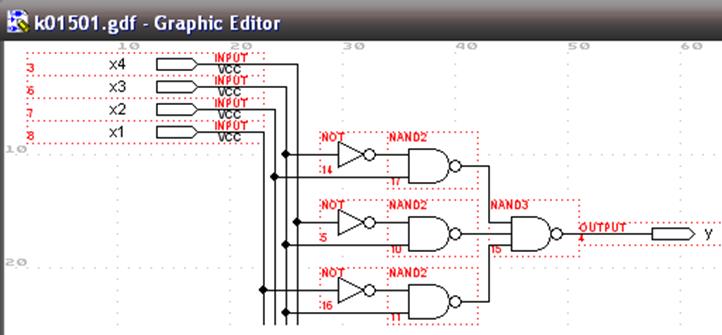
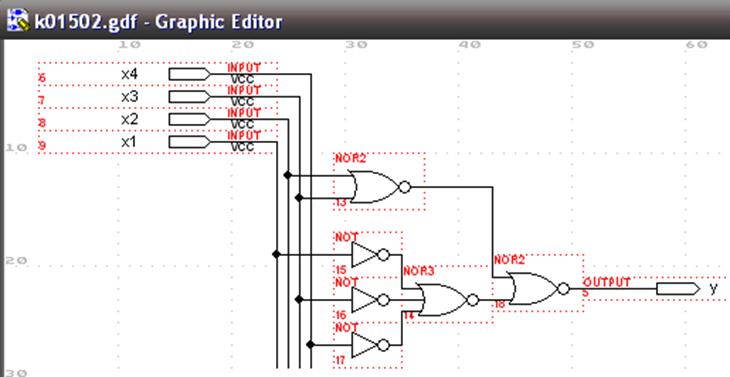
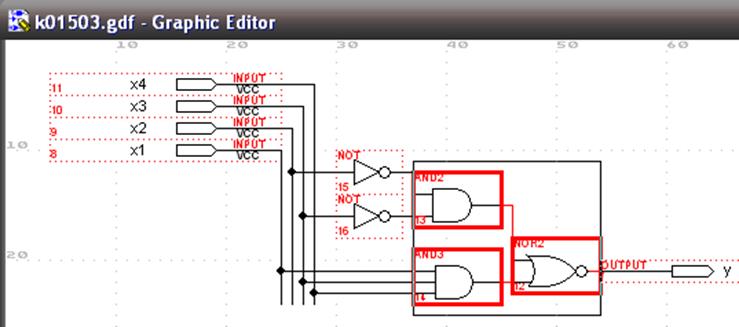
Рисунок 1.8 – Зображення реалізацій в графічному редакторі
На рис. 1.8 виділено комбінований логічний елемент 2-3І-2АБО-НЕ, який складається з елементарної логіки і необхідний для реалізації функції в булевому базисі.
Проаналізуємо швидкодію пристрою за допомогою матриці затримок:
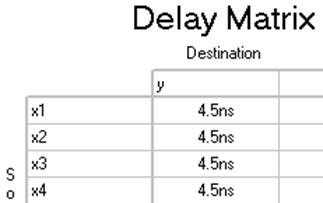
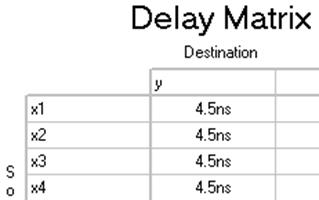
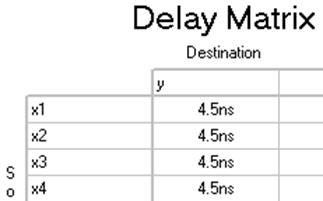
Рисунок 1.9 – Матриці затримок реалізацій
З рис. 1.9 видно, що затримка вихідного сигналу від вхідних для всіх трьох реалізацій однакова і становить 4,5нс; це відповідає стандартній затримці віртуального мікропроцесора MAX+Plus.
Знімаємо часові діаграми реалізацій:
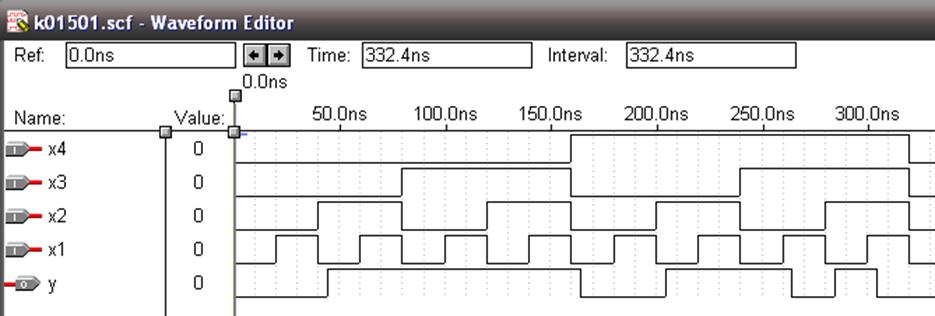
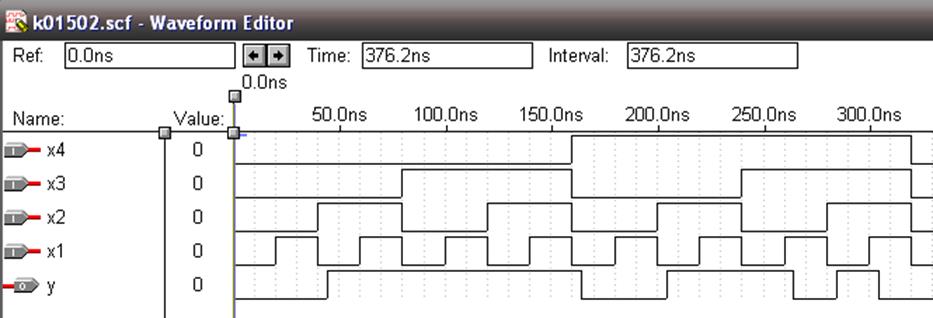
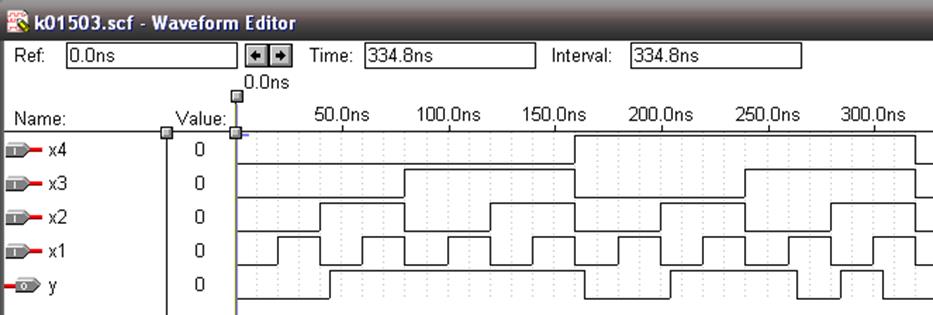
Рисунок 1.10 – Часові діаграми реалізацій
З рис. 1.10 видно, що часові діаграми всіх реалізацій співпадають. Можна зробити висновок, що проектування виконано правильно.
1.6 Автоматичне проектування пристрою в текстовому редакторі MAX+Plus II
Створюємо текстовий файл, який має містити початкову неспрощену функцію з метою перевірки правильності спрощення та мінімізації:
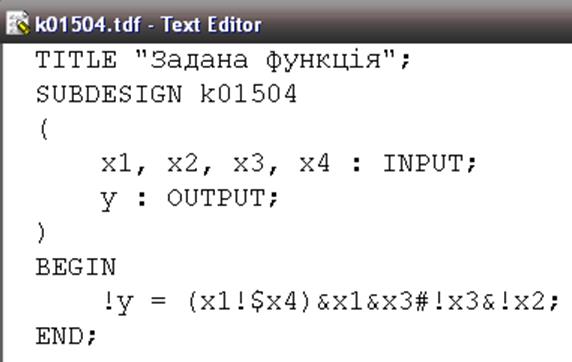
Рисунок 1.11 – Текстовий файл з описом функції
Компілюємо проект, а потім автоматично порівняємо результати, наприклад, з часовими діаграмами реалізації в базисі І-НЕ:
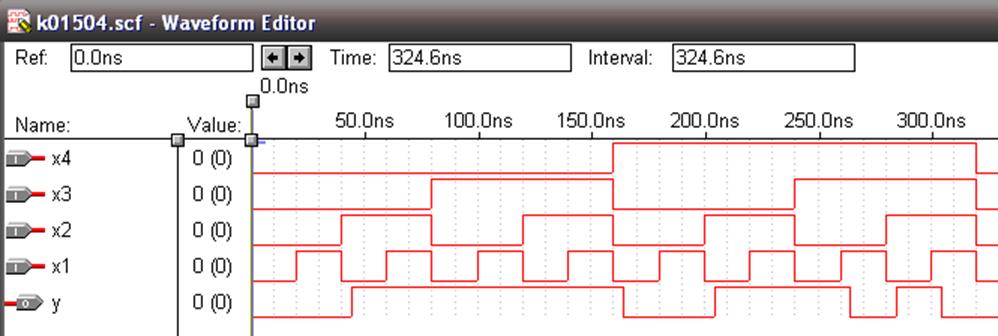
Рисунок 1.12 – Автоматичне порівняння результатів
Порівняння здійснюється автоматично вбудованою підпрограмою. При цьому ділянка діаграми, яка однакова в обох файлах, відображається червоним кольором; навпаки – чорним. Результати повністю збігаються, як і було спроектовано. Це підтверджує відповідність, однозначність і правильність спрощень, мінімізації та реалізації в різних базисах.
2 ПРОЕКТУВАННЯ ПРИСТРОЮ НА ЦКП
2.1 Синтез порогового елемента
Варіантом завдання передбачено розробити пороговий елемент «3 з 6». Для побудови використаємо одно- та дворозрядні суматори.
Оскільки входів – шість, використаємо три суматори: два однорозрядних – для підрахунку суми однорозрядних чисел, і один дворозрядний – для підсумовування двох дворозрядних чисел. Схема приведена на рис. 2.1.
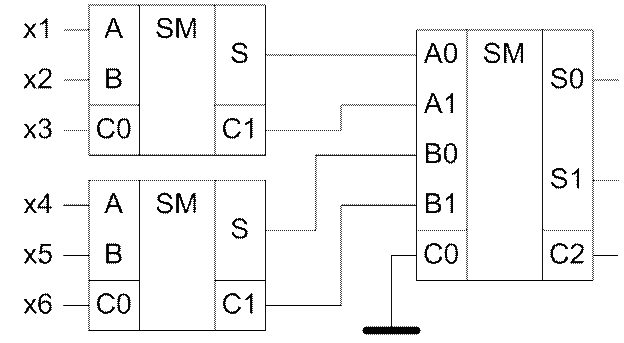
Рисунок 2.1 – Схема суматора шести однорозрядних чисел
На виході такого суматора отримаємо трирозрядне число C2S1S0, яке може приймати значення від 000 до 110. Задана функція у повинна приймати значення «1» тоді, коли хоча б на трьох з шести входів діють рівні логічної «1». Побудуємо таблицю відповідності функції:
Таблиця 2.1 – Таблиця відповідності
|
C2 |
S1 |
S0 |
y |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
х |
Мінімізуємо функцію, побудувавши попередньо карту Карно:
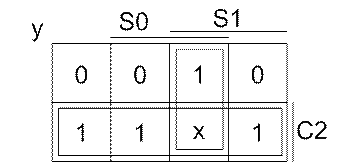
Рисунок 2.2 – Карта Карно
Зчитуємо з карти Карно функцію:
![]()
За результатами будуємо остаточну схему:
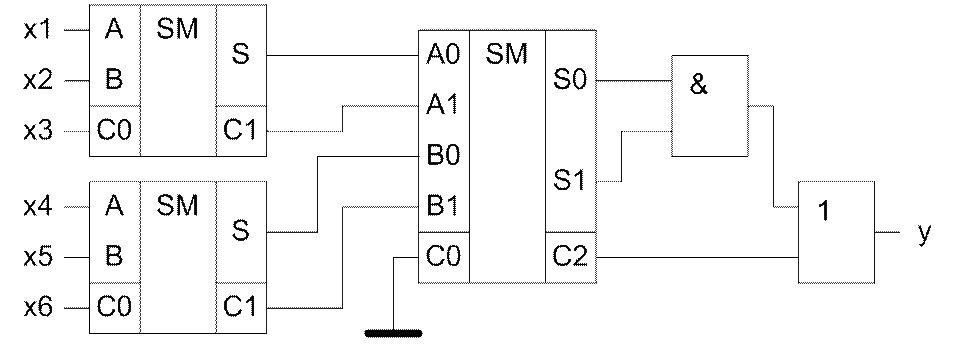
Рисунок 2.3 – Схема порогового елемента
2.2 Автоматичне проектування пристрою у графічному редакторі MAX+Plus
Створюємо графічний файл зі схемою порогового елемента:
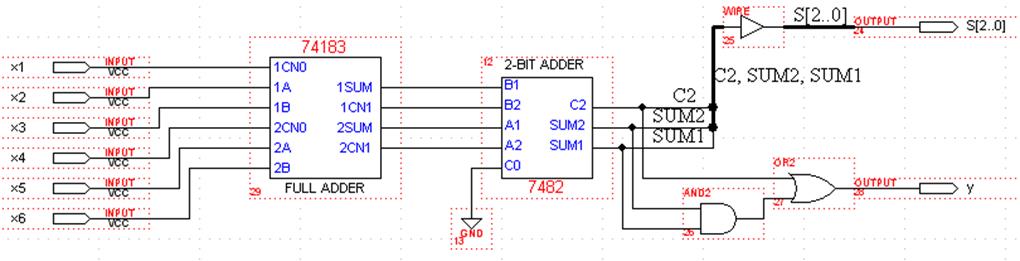
Рисунок 2.4 – Зображення порогового елемента в графічному редакторі
Компілюючи проект, отримаємо результати:
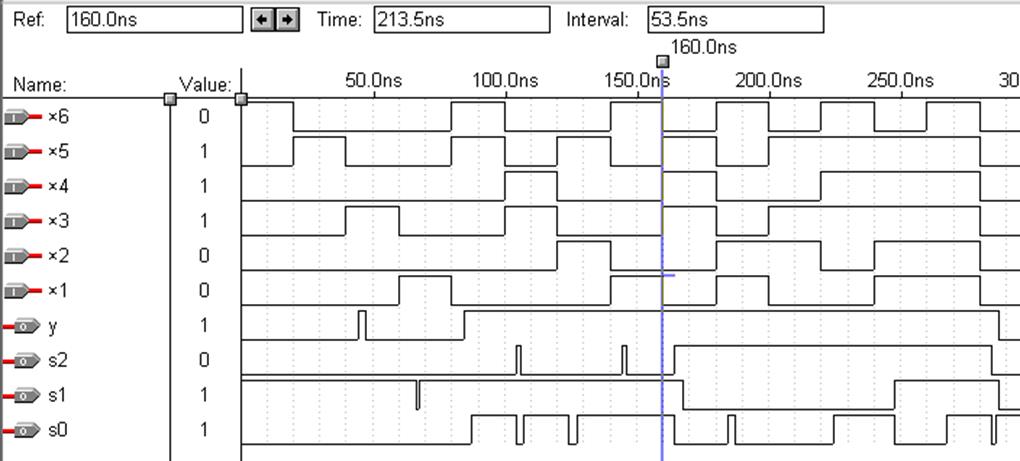
Рисунок 2.5 – Часові діаграми пристрою
Легко переконатися з рис. 2.5, що пристрій працює так, як заплановано.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.