Для
логічної функції ![]() наведемо досконалу форму
(ДДНФ та ДКНФ) і таблицю відповідності.
наведемо досконалу форму
(ДДНФ та ДКНФ) і таблицю відповідності.
Мінімізуємо логічну функцію Y за допомогою еквівалентних перетворень на основі властивостей алгебри логіки:
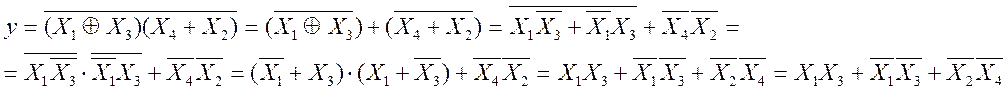
Складемо таблицю відповідності для спрощеної функції: Таблиця 1
|
i |
X4 |
X3 |
X2 |
X1 |
|
|
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
2 |
0 |
0 |
1 |
0 |
1 |
0 |
|
3 |
0 |
0 |
1 |
1 |
0 |
1 |
|
4 |
0 |
1 |
0 |
0 |
1 |
0 |
|
5 |
0 |
1 |
0 |
1 |
1 |
0 |
|
6 |
0 |
1 |
1 |
0 |
0 |
1 |
|
7 |
0 |
1 |
1 |
1 |
1 |
0 |
|
8 |
1 |
0 |
0 |
0 |
1 |
0 |
|
9 |
1 |
0 |
0 |
1 |
0 |
1 |
|
10 |
1 |
0 |
1 |
0 |
1 |
0 |
|
11 |
1 |
0 |
1 |
1 |
0 |
1 |
|
12 |
1 |
1 |
0 |
0 |
0 |
1 |
|
13 |
1 |
1 |
0 |
1 |
1 |
0 |
|
14 |
1 |
1 |
1 |
0 |
0 |
1 |
|
15 |
1 |
1 |
1 |
1 |
1 |
0 |
По складеній таблиці наведемо вирази для логічної функції Y у досконалих формах:
ДДНФ:
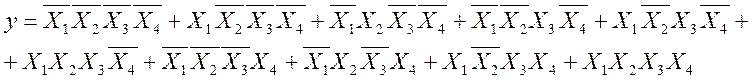
ДКНФ:
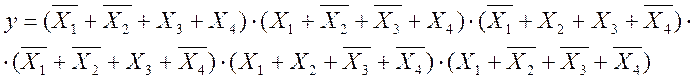
1.2 Мінімізація функції у формах МДНФ/МКНФ (для прямої та інверсної функції) та реалізація у базисах І-НЕ, АБО-НЕ, І-АБО-НЕ
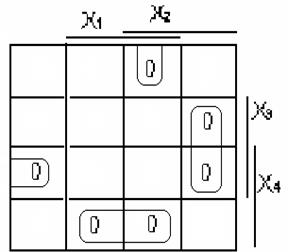
По отриманій таблиці відповідності для знаходження МДНФ і МКНФ складемо відповідні діаграми термів:
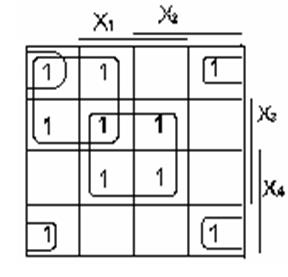
![]()
![]()
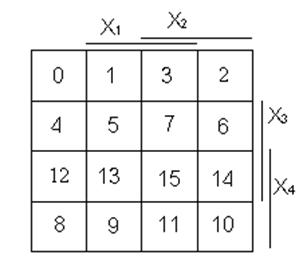
а) б) в)
Рисунок 1- Діаграми термів для логічної функції
Запишемо результати об’єднань (рисунок 1, б) у вигляді МДНФ для прямої та інверсної функцій:
Пряма МДНФ: ![]()
Інверсна МДНФ: ![]()
Запишемо результати об’єднань (рисунок 1, в) у вигляді МКНФ для прямої та інверсної функцій:
Пряма МКНФ: ![]()
Інверсна МКНФ:![]()
Реалізація функції в базисі І-НЕ
Мінімізуємо функцію в МДНФ, за законом де Моргана переходимо від сум до добутків за формулою:
![]() ;
;
![]()
![]()
Відобразимо структурну схему отриманої функції.
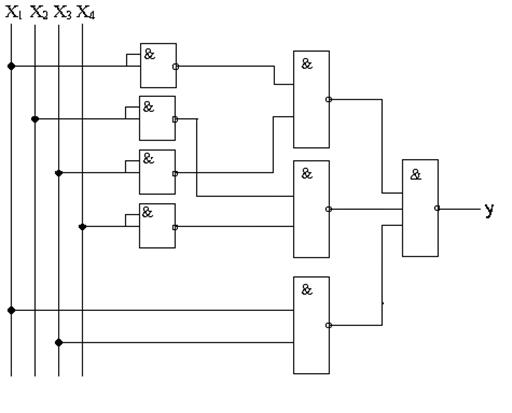
Рисунок 2- Структурна схема функції в базисі І-НЕ
В результаті видно, що складність даної схеми, становить: 8/13
Реалізація функції в базисі АБО-НЕ
Мінімізуємо функцію в МКНФ, за законом де Моргана переходимо від добутків до сум за формулою:
![]() ;
;
![]()
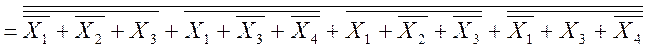
Відобразимо структурну схему отриманої функції:
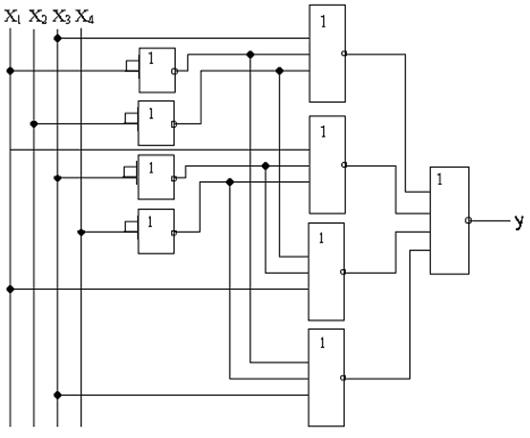
Рисунок 3 - Структурна схема функції в базисі АБО-НЕ
В результаті видно, що складність даної схеми, становить: 9/20.
Реалізація функції в базисі І-АБО-НЕ
Мінімізуємо функцію![]() в МДНФ, за
аксіомою двоїстості переходимо до базису за формулами:
в МДНФ, за
аксіомою двоїстості переходимо до базису за формулами:
![]() ;
; ![]() ;
;
![]() ;
;
![]()
Відобразимо структурну схему отриманої функції:
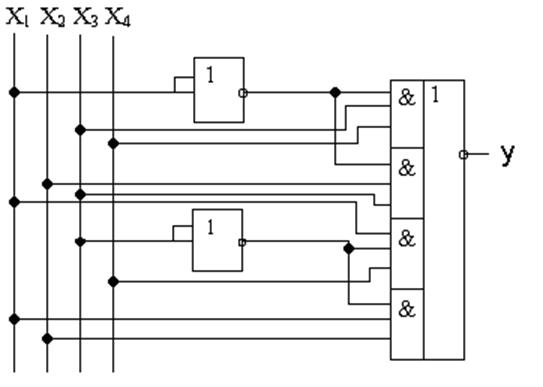
Рисунок 4 - Структурна схема функції в базисі І-АБО-НЕ
В результаті видно, що складність даної схеми, становить: 3/14
1.3 Мінімізація функції із застосуванням редукції
Мінімізуємо схему в елементному базисі АБО-НЕ.
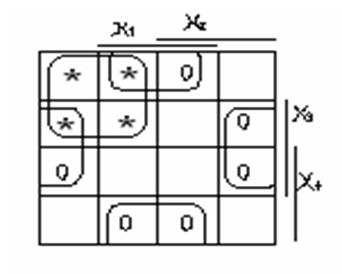
Рисунок 5 – Діаграми термів для мінімізації схеми
Понизимо складність схеми додаванням нулів (рисунок 5), утворене об’єднання D є більш простим для мінімізації:
![]()
![]()
![]()
![]()
![]() +
+![]() =
= ![]()
![]()
Відобразимо структурну схему отриманої функції:
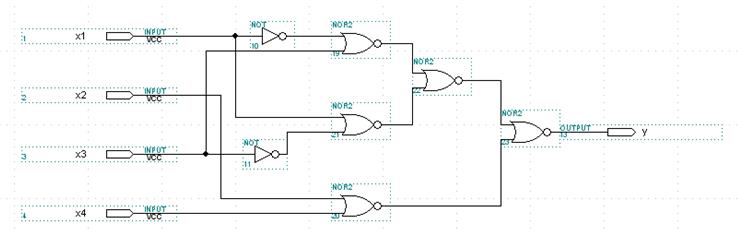 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.