Замыкание множества заданных функциональных зависимостей, страница 3

R2                   восстанавливающего R.

2. На условие принадлежности полученных функциональных зависимостей к множеству F⁺.

Задача принадлежности функциональной зависимости к F⁺ была решена с помощью простого алгоритма. Вместо вычисления F⁺ можно вычислить другое множество, которое будет называться X⁺ и функциональная зависимость x→y принадлежит F⁺, если y≤x⁺.

Алгоритм получения X⁺.

Рассмотрим на примере:

            Дано: U={A,B,C,D,E,G} и R(A,B,C,D,E,G).

Пусть F состоит из следующих восьми зависимостей:

            F={     AB→C          D→EG

                            C→A          BE→C

                         BC→D          CG→BD

                   ABCD→B          CE→AG}

            Проверим, принадлежит ли BD→E к F⁺.

                        Положим X⁽⁰⁾= BD.

1.Вычислим значение X⁽¹⁾. Для его вычисления найдем зависимости, которые имеют в левой части B, D или BD. Такой зависимостью является: D→EG.

                        Присоединим к X⁽⁰⁾ EG (правую часть зависимости), тогда X⁽¹⁾= BDEG.

2.Ищем зависимости, которые в левой части имеют B,D,E,G или их комбинации.

                        D→EG, BE→C. Тогда X⁽²⁾ = BCDEG

3.Выписываем зависимости, имеющие в левых частях B,C,D,E,G.

                        C→A, BC→D, CG→,BD, CE→AG. X⁽³⁾ = ABCDEG – мы получили множество всех атрибутов отношения R. Значит следующие шаги не принесут никаких новых результатов. Итеративный процесс на этом заканчивается.

X⁺ = ABCDEG       (BD)⁺ = ABCDEG

Проверим теперь:  Принадлежит ли зависимость BD→E зависимости F⁺.

            Т.к. Е ≥X⁺, то зависимость BD→E принадлежит F⁺ замыканию множества функциональных зависимостей F.

4.7. Правила вывода функциональных зависимостей.

            Пусть U – универсально множество атрибутов, т.е. полный набор атрибутов отношения R.

            А1,…..,An – атрибуты отношения R, тогда: U={A1,A2,…,An} схема отношения R{A1,A2,A3,….,An}.

Задано множество функциональных зависимостей F={F1,F2,F3,…,Fk}.

Правило-F11.Рефлекторность.

            Если x≤U, y≤U, y≤x , то функциональная зависимость x → y следует из F.

Имея исходную функциональную зависимость можно:

1.  В состав левой части вводить любые атрибуты из U, при этом функциональная зависимость нарушаться не будет.

2.  Добавлять атрибуты из U в состав атрибутов правой части, при этом нужно следить, чтобы добавленный атрибут уже находился в левой части выражения функциональной зависимости.

3.  Удалять атрибуты из правой части, при этом зависимость будет сохраняться,

4.  Удалять атрибуты из левой части, при этом необходимо следить за тем, что бы удаляемый атрибут отсутствовал и в правой части.

Пример:

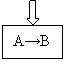
            Если A         → B

 

            То из A2 → B, следует

 

Если присутствуют две зависимости    A2→B

                                                           и      A  →B , то

A→B

                                                                                  - избыточная зависимость