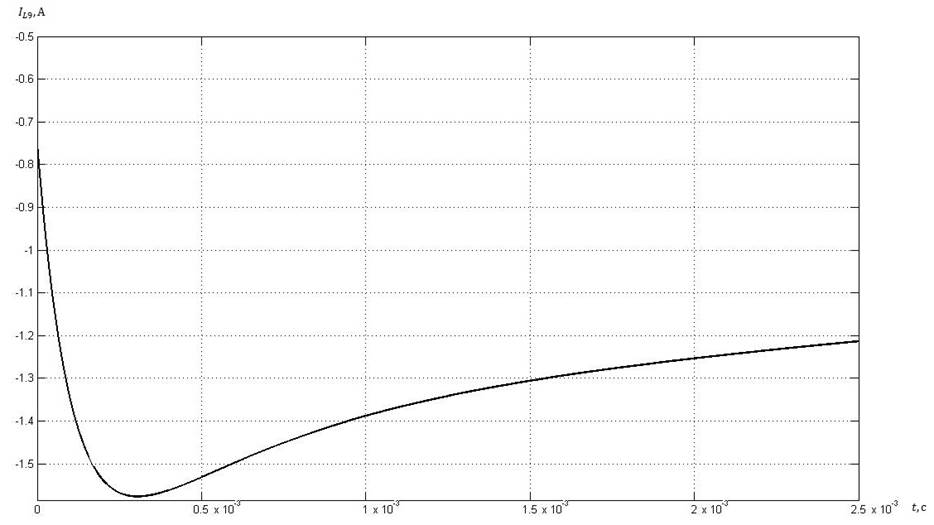
Электротехника \ Теоретические основы электротехники

Расчет переходных процессов в линейных электрических цепях с сосредоточенными параметрами, страница 2

Рис. 6. Ток в индуктивности девятой ветви (с увеличенным первым участком).

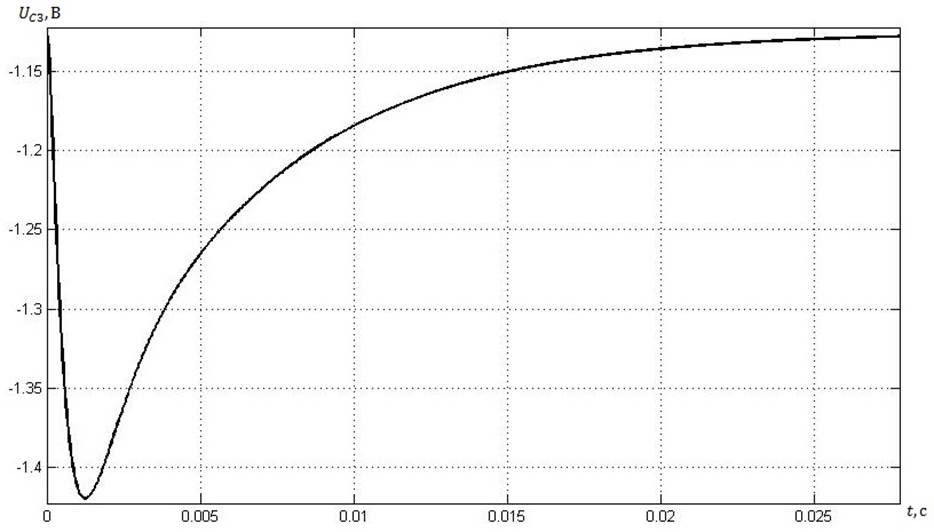
Рис. 7. Напряжение на конденсаторе третьей ветви.

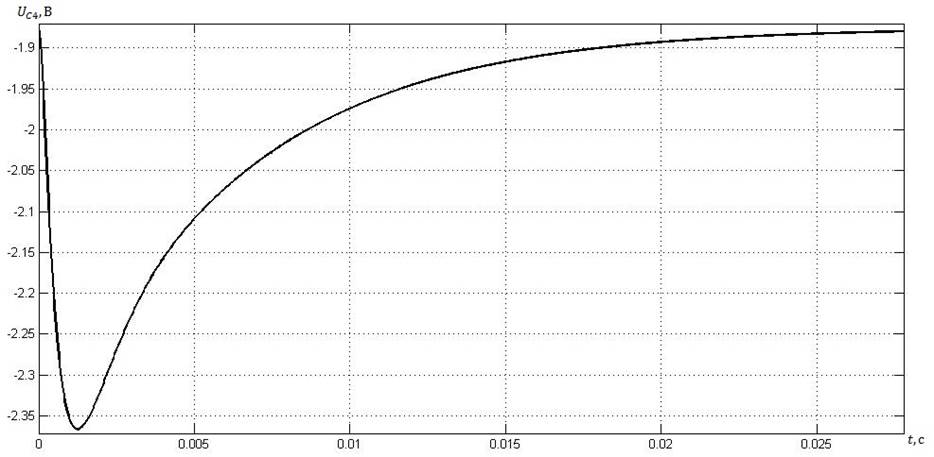
Рис. 8. Напряжение на конденсаторе четвертой ветви.

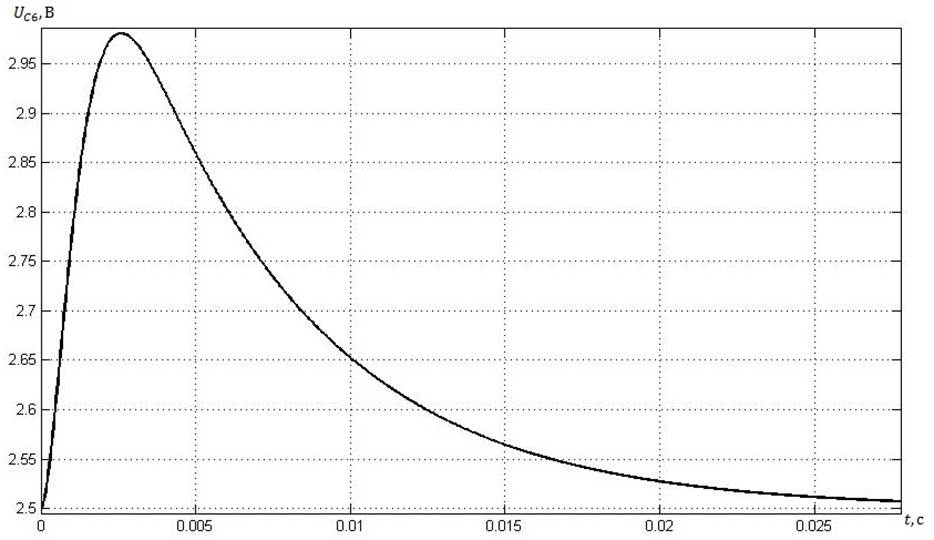
Рис. 9. Напряжение на конденсаторе шестой ветви.

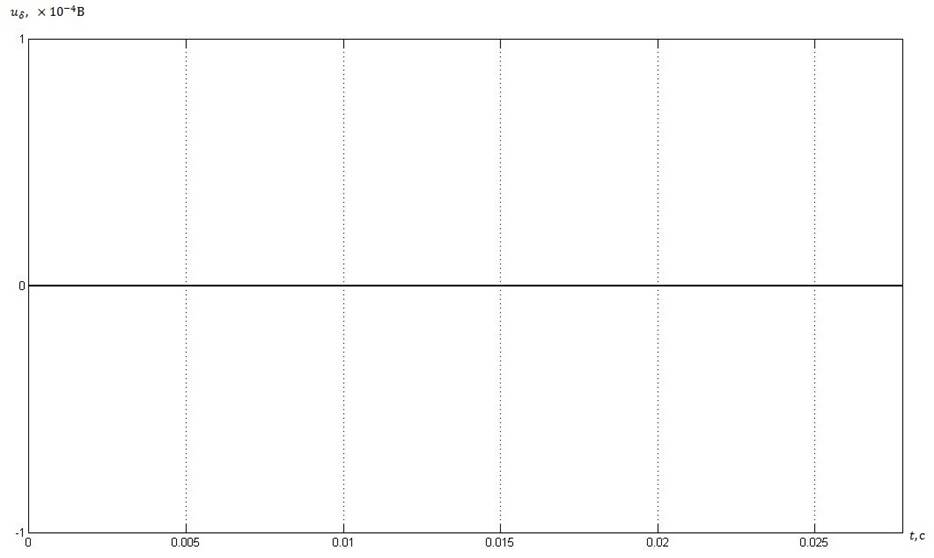
Рис. 10. График невязки уравнения по II з-ну Кирхгофа для контура, состоящего из ветвей 3-4-5-6-10.

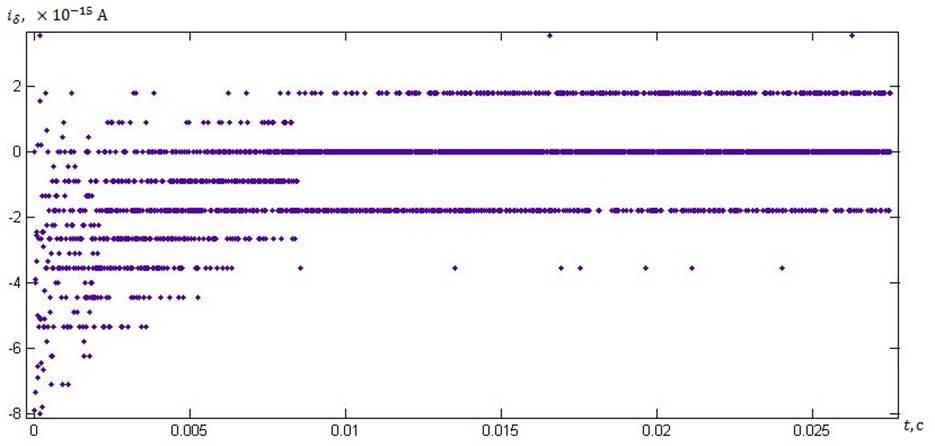
Рис. 11. График невязки уравнения по I з-ну Кирхгофа для узла 1.

Установившиеся значения токов в катушках и напряжений на конденсаторах:

;

;

;

;

;

.

3.  Расчет цепи после коммутации (расчет конечных условий).

Расчет конечных условий производится с целью проверки результатов, полученных с использованием метода синтетических схем.

Как видно из рис.3, граф цепи является несвязным. Причем левая цепь аналогична цепи, расчет которой произведен в п.1. Определив значение тока в ветви 7 и, использую полученные в п.1. результаты, можно определить конечные условия.

Ток 7ой ветви (рис.3): .

В нумерации исходной схемы цепи:

.

;

;

;

;

;

.


Вывод: 

Метод синтетических схем является приближенным методом, что объясняет различия в конечных условиях, полученных во 2 и в 3 пунктах. Уменьшив шаг интегрирования, можно добиться большей точности расчетов, однако это требует больших ресурсов ЭВМ.

интегрирования.

Таблица № 4.

Зависимость точности расчета от шага и времени интегрирования.

Параметр

Результаты    п. 3

Il7

9,1670

9,2483

9,25

Il8

-12,4070

-12,4981

-12,5

Il9

-0,7570

-0,7501

-0,75

Uc3

-1,1280

-1,1251

-1,125

Uc4

-1,8800

-1,8751

-1,875

Uc6

2,5080

2,5002

2,5

Приложение №1.

Листинг программы расчета установившихся режимов в цепях постоянного тока MS.

function [I,U]=MS(NETlist)

%Функция позволяет произвести расчет эл. цепи матричным методом по методу

%сечений. Цепь не должна содержать идеальных источников ЭДС.

%Аргументы:

%f (число)- угловая частота источников питания, Гц.

%Netlist (строка)- имя файла, содержащего информацию о конфигурации цепи.

%Выходные параметры:

%I (вектор-столбец)- внутренние токи ветвей.

%U (вектор-столбец)- внутренние напряжения ветвей.

NET=dlmread(NETlist,';',1,0);

p=max(NET(:,1));

q=max([max(NET(:,2)) max(NET(:,3))]);

A=zeros(q,p);

for k=1:p

    A(NET(k,2),k)=1;

    A(NET(k,3),k)=-1;

    Y(k,k)=1/(NET(k,4));

    J(k,1)=NET(k,6);

    E(k,1)=NET(k,5);

end

A(q,:)=[];

Atree=A(:,1:(q-1));

Alink=A(:,q:p);

F=-(inv(Atree)*Alink).';

D=diag(ones(1,q-1));

D(:,q:p)=-F.';

W=D*Y*(D.');

B=-D*(J+Y*E);

Utreeext=inv(W)*B;

Uext=(D.')*Utreeext;

U=Uext+E;

I=Y*U;


Приложение №2.

Листинг программы расчета переходных процессов Transients.

function [h,T,Xaxis,Currents,Voltages]=Transients(NETlist)

%Функция позволяет произвести расчет переходных процессов в эл. цепи пост.

%тока. Цепь не должна содержать идеальных источников ЭДС.

%Аргументы:

%Netlist (строка)- имя файла, содержащего информацию о конфигурации цепи.

%Выходные параметры:

%h - шаг интегрирования

%T - время интегрирования

%Xaxis (вектор-строка) - отсчет времени

%Currents - токи в катушках индуктивности на каждом шаге (в соотв. с Xaxis)

%Voltages - напр. на конденсаторах на каждом шаге (в соотв. с Xaxis)

NET=dlmread(NETlist,';',1,0);

p=max(NET(:,1));                            %количество ветвей

q=max([max(NET(:,2)) max(NET(:,3))]);       %количество узлов

Rmax=max(NET(:,4));

Rmin=max(NET(:,4));

Lmax=max(NET(:,5));

Lmin=max(NET(:,5));

Cmax=max(NET(:,6));

Cmin=max(NET(:,6));

for k=1:p

    if (NET(k,4) < Rmin) && (NET(k,4)~=0), Rmin=NET(k,4);end

    if (NET(k,5) < Lmin) && (NET(k,5)~=0), Lmin=NET(k,5);end

    if (NET(k,6) < Cmin) && (NET(k,6)~=0), Cmin=NET(k,6);end

end

Tmin=min([Lmin/Rmax Rmin*Cmin]);

Tmax=max([Lmax/Rmin Rmax*Cmax]);

h=0.05*Tmin;                                 %шаг интегрирования

T=10*Tmax;                                   %время интегрирования

A=zeros(q,p);

I=zeros(p,1);

Uc=zeros(p,1);

for k=1:p

    A(NET(k,2),k)=1;

    A(NET(k,3),k)=-1;

    if NET(k,5)~=0

        Y(k,k)=h/(NET(k,5)+h*NET(k,4));

        Jkoef(k,1)=NET(k,5)/(NET(k,5)+h*NET(k,4));

        J(k,1)=NET(k,9).*Jkoef(k,1);

        I(k,1)=NET(k,9);

    elseif NET(k,6)~=0

        Y(k,k)=1/(NET(k,4)*(1+h/(NET(k,6)*NET(k,4))));

        J(k,1)=-NET(k,9)*Y(k,k);

        Uc(k,1)=NET(k,9);

    elseif NET(k,4)~=0

        Y(k,k)=1/NET(k,4);

        J(k,1)=NET(k,8);

    else

        Y(k,k)=0;

        J(k,1)=NET(k,8);

    end

    E(k,1)=NET(k,7);

 end

A(q,:)=[];                               %м-ца соединений

W=inv(A*Y*(A.'));                        %м-ца узловых проводимостей

t=0;

Xaxis=[t];

Currents=[I];

Voltages=[Uc];

while (t < T)

    B=-A*(J+Y*E);                            %м-ца задающих токов узлов

    U0=W*B;                                  %потенциалы узлов

    Uext=(A.')*U0;                           %внешние напр. ветвей

    U=Uext+E;                                %внутренние напряжения ветвей

    I=Y*U;                                   %внутренние токи ветвей

    Iext=I+J;                                %внешние токи ветвей

    Uc=Uext-Iext.*NET(:,4);

    for k=1:p

        if NET(k,5)~=0

            J(k,1)=Iext(k,1).*Jkoef(k,1);

        elseif NET(k,6)~=0

            J(k,1)=-Uc(k,1)*Y(k,k);

        end

    end

    t=t+h;

    Xaxis=[Xaxis t];

    Currents=[Currents, Iext];

    Voltages=[Voltages, Uc];

end

Скачать файл