Таблица 6. Соответствие первоначальных ветвей новым.
|
Номер ветви на схеме 1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Соответствующий номер на схеме 5 |
1 |
2 |
12 |
8 |
7 |
9 |
10 |
11 |
4 |
5 |
6 |
3 |
Для
расчета цепи на каждом шаге интегрирования в функции perpr используется метод узловых потенциалов. Для
составления синтетических схем используются ![]() -модели
реактивных элементов цепи.
-модели
реактивных элементов цепи.
Алгоритм работы функции perpr:
1) чтение данных о конфигурации цепи;
2) Выделение матрицы сопротивления![]() ,
индуктивности
,
индуктивности![]() ,
ёмкости
,
ёмкости![]() ,
ЭДС
,
ЭДС![]() ,
источников тока
,
источников тока![]() .
.
3) Расчёт количества ветвей p, узлов q и связей n.
4) Поиск максимальных и минимальных
значений ![]() .
.
5) Расчет шага интегрирования ![]() и времени интегрирования
и времени интегрирования ![]() ;
;
6) Составление матрицы соединений ![]() ,
матрицы проводимостей ветвей
,
матрицы проводимостей ветвей ![]() ,
матрицы источников тока
,
матрицы источников тока ![]() ,
матрицы источников ЭДС
,
матрицы источников ЭДС ![]() для
синтетической схемы цепи;
для
синтетической схемы цепи;
7) нахождение матрицы, обратной
матрице ![]() , из выражения:
, из выражения: ![]() ;
;
8) циклический расчет синтетических схем (рекурсия):
1. нахождение матрицы ![]() из
выражения:
из
выражения: ![]() ;
;
2. нахождение матрицы узловых
потенциалов: ![]() ;
;
3. нахождение матрицы внешних
напряжений ветвей: ![]() ;
;
4. нахождение матрицы внутренних
напряжений: ![]() ;
;
5. нахождение матрицы внутренних
токов: ![]() ;
;
6. нахождение матрицы внешних токов:
![]() ;
;
7. формирование матрицы источников
тока ![]() для
следующего цикла расчета.
для
следующего цикла расчета.
9) Построение графиков токов и напряжений.
Шаг интегрирования ![]() .
.
Время интегрирования ![]() .
.
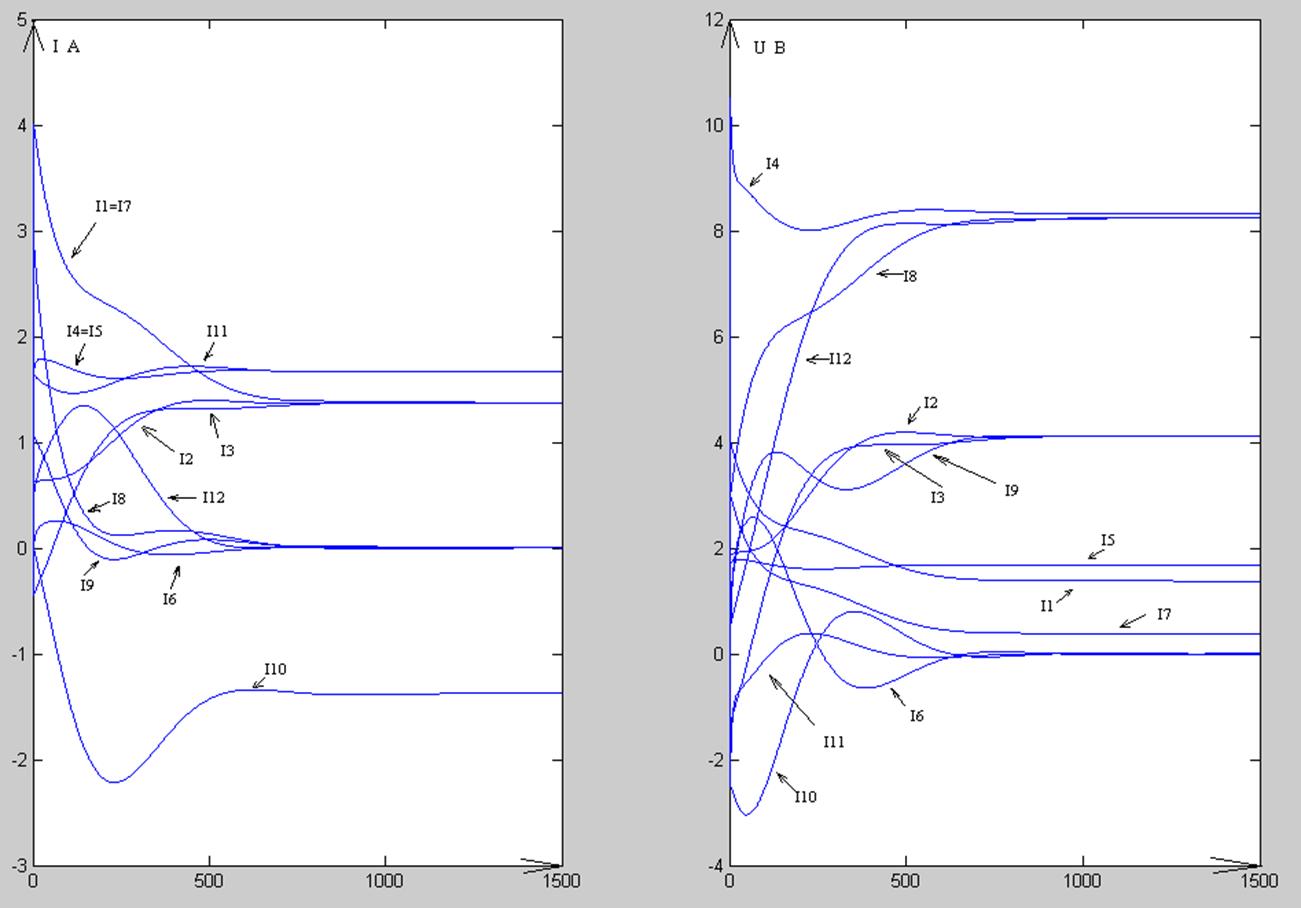
Рисунок 8. Данные по переходному процессу полученные в результате рекурсии. Значение тока и напряжения на каждом шаге расчёта.
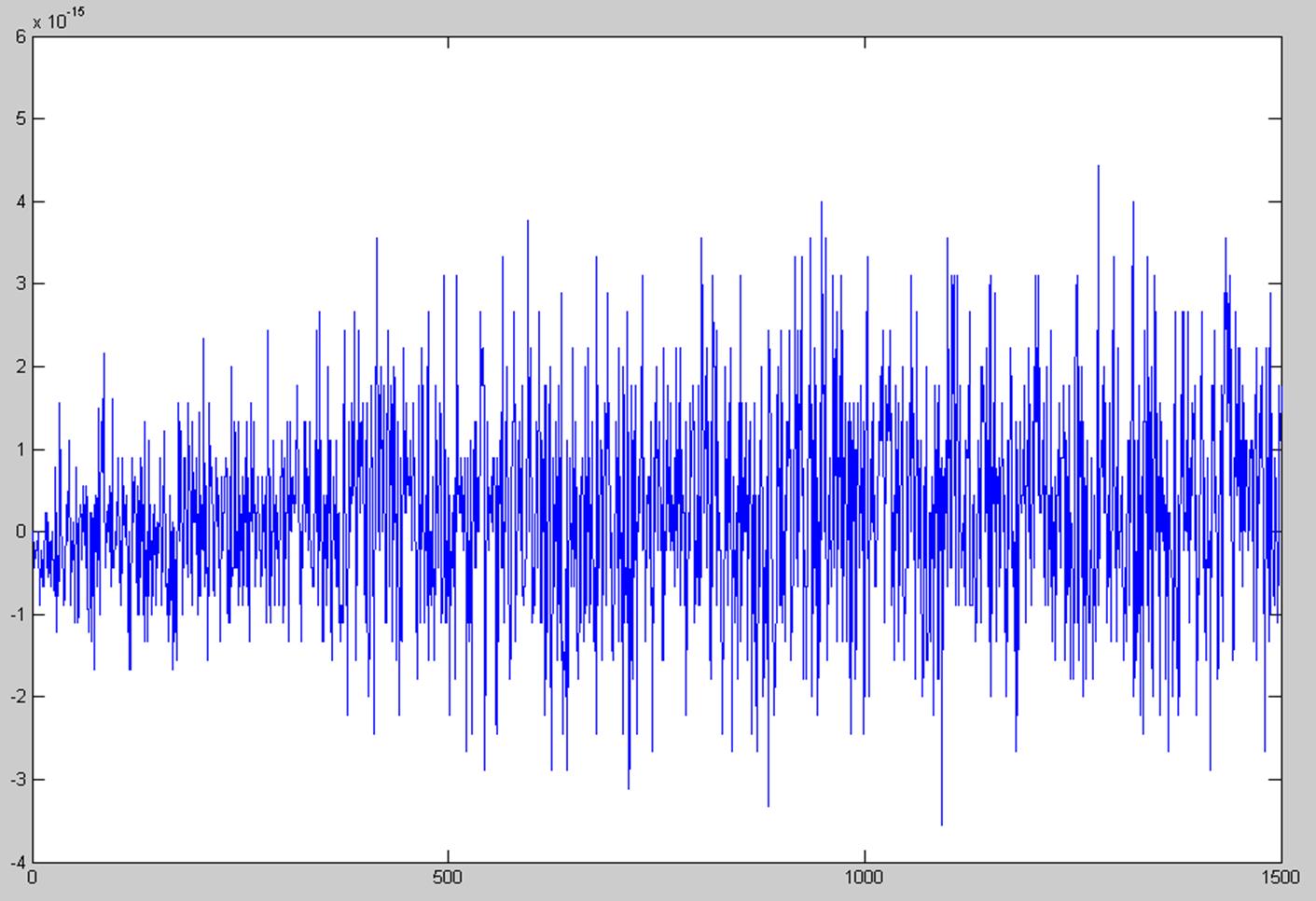
Рисунок 9. График невязки уравнения по I закону Кирхгофа для узла 2.
Рисунок 10. График невязки уравнения по 2 закону Кирхгофа для контура, состоящего из ветвей 3, 10 и 9 .
Вывод.
Метод синтетических схем является наиболее удобным и простым, из тех, что можно реализовать на компьютере, способом оценки влияния переходного процесса на значения токов в цепи.
Но он не даёт абсолютно точного значения, только приближённые. Это хорошо представлено на рисунке 2(невязка во 2-ом узле).
Как показывают результаты расчёта, показания могут меняться при изменении шага интегрирования и для улучшения данных можно уменьшить шаг интегрирования.
Таблица
7. Данные полученные при шаге интегрирования ![]()
|
Номер ветви |
I А |
U В |
|
1 |
1,37519038660255 |
1,37519038660255 |
|
2 |
1,37482663516640 |
4,12447990549921 |
|
3 |
1,37483571816529 |
4,12450715449587 |
|
4 |
1,66668339028265 |
8,33335682198105 |
|
5 |
1,66668339028267 |
1,66668339028267 |
|
6 |
5,91954536105277e-05 |
0,000591954536105277 |
|
7 |
1,37519038660255 |
0,375190386602547 |
|
8 |
2,91281372764018e-05 |
8,24961922679491 |
|
9 |
-9,08299889124109e-06 |
4,12513932129570 |
|
10 |
-1,37511114601055 |
-0,000632166799825917 |
|
11 |
1,66662419482904 |
-4,02122637206404e-05 |
|
12 |
0,000334623298870795 |
8,24898705999508 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.