Построение теней в ортогональных проекциях: Методические указания и варианты заданий расчетно-графической работы по курсу «Начертательная геометрия. Инженерная графика», страница 2

Положение прямой	Чертеж	Запись	Вывод
1	2	3	4
Прямая параллельна плоскости		АВ || П2 АТ2ВТ2|| АВ АТ2ВТ2= АВ	Тень отрезка прямой, параллельной плоскости, равна и параллельна самому отрезку.
Прямая перпендикулярна плоскости		АВ^П1 АТ1ВТ1ºS1	Тень отрезка прямой, перпендикулярной плоскости, совпадает с проекцией светового луча на эту плоскость.
Прямая лежит в лучевой плоскости		АВ Î Т Т^ П1 АТ2ВТ2ÎТП2 ТП2^ ох	Тень отрезка прямой, лежащей в лучевой плоскости, совпадает с вертикальным следом этой плоскости.

Продолжение табл. 1

1	2	3	4
Прямая совпадает с направлением светового луча		АВºS АТºВТ	Тень прямой, совпадающей с направлением светового луча, вырождается в точку.

2.5. Собственные тени цилиндрических

и конических поверхностей

С усложнением в настоящее время архитектурных форм возникает необходимость определения границ собственной тени их поверхностей.

Для поверхностей вращения удобнее всего определять границы собственной тени способом профессора Колотова С.М. без использования плана. Им разработана схема построения границ собственной тени конуса с различными углами наклона образующих к плоскости основания (см. рис. 7–10).

Последовательность построения границ собственной тени на конусе с углом наклона образующей к горизонтальному основанию α следующая (рис. 7):

1)  в пересечении оси конуса с окружностью совмещенного основания находится точка А;

2)  проводится прямая АК параллельная левой контурной образующей;

3)  из точки К проводятся лучи К2₀ и К1₀ под углами 45^° к основанию;

4)  точки 1₀ и 2₀ проецируются на основание конуса. S1 и S2 – теневые образующие (границы собственной тени) боковой поверхности конуса.

На рис. 7 показано построение контуров собственной тени для угла α > 45°.

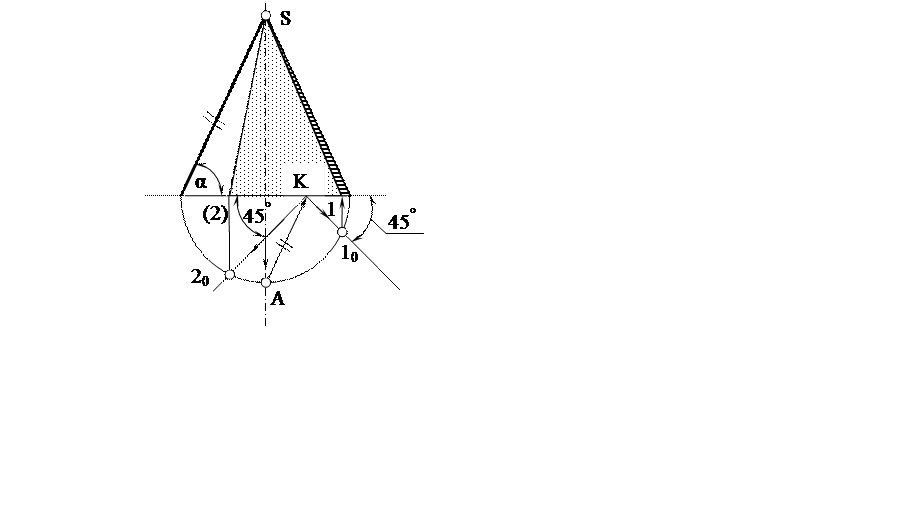
Рис. 7

Если α = 45^°, то в собственной тени оказывается 1/4 часть боковой поверхности конуса (рис. 8).

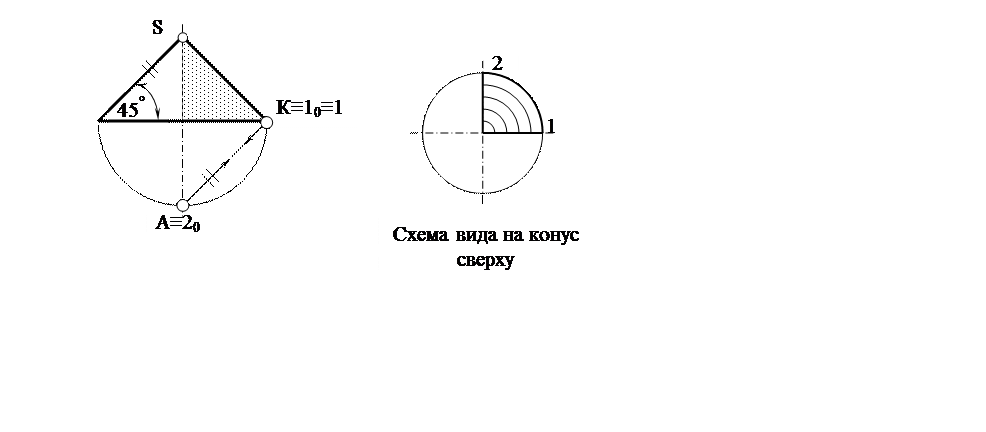
Рис. 8

Если α = 35^°= Θ (световой угол), тень собственная вырождается в прямую линию (рис. 9).

Если α < 35^° вся боковая поверхность конуса освещена. Все рассмотренные конические поверхности располагаются вершинами вверх.

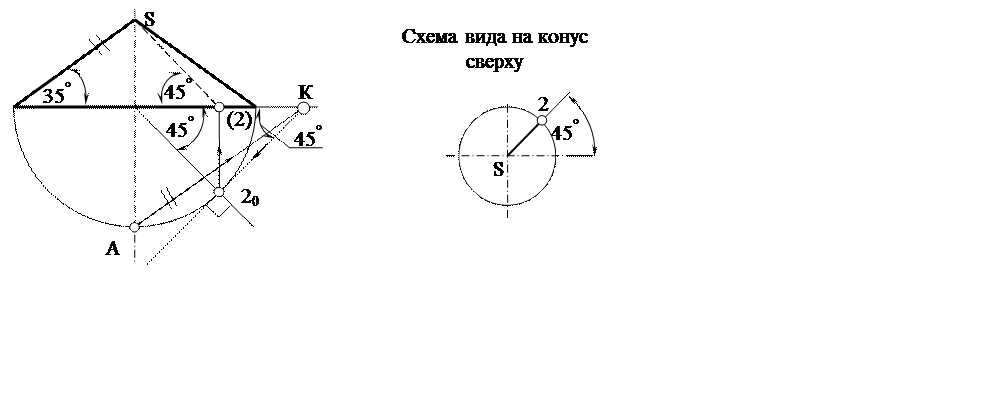
Рис. 9

Если α = 90^°, то коническая поверхность вырождается в цилиндрическую (рис. 10).

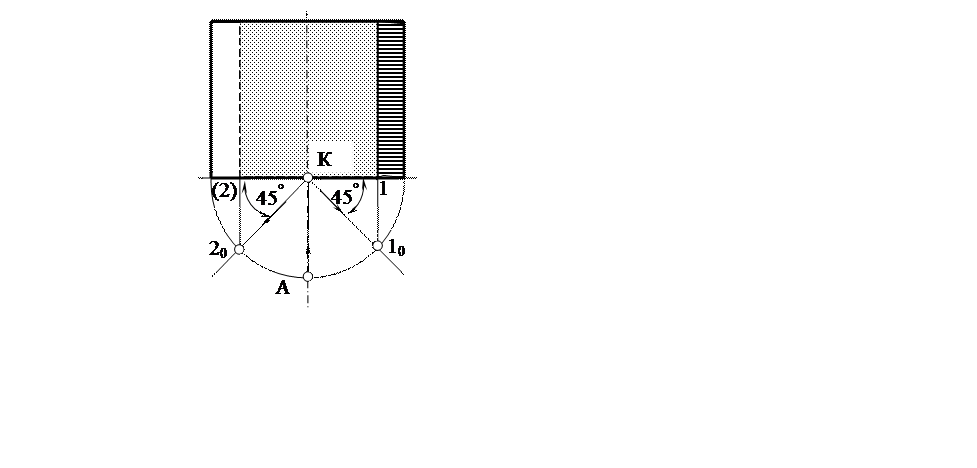
Рис. 10

Рассмотренные выше построения используются при определении границ собственной тени любой поверхности вращения методом описанных конических поверхностей.

Суть метода состоит в том, что около тела вращения описывается ряд конических поверхностей с различным углом α. Конические поверхности касаются данного тела вращения по окружностям, которые принимаются за основания конусов. На этих окружностях определяют пары точек, принадлежащие собственной тени описанных конусов. Соединяют точки, полученные для каждого из описанных конусов в линию, которая и будет являться контуром собственной тени тела.

3. ПОСТРОЕНИЕ ТЕНЕЙ СООРУЖЕНИЯ

При построении теней рекомендуется следующая последовательность:

1. Определяются границы собственной тени сооружения.

2. Строятся контуры падающей тени.

Пример 1. В приведённом на рис. 7 примере не освещены солнцем только плоскость основания сооружения и вертикальные грани AA^/BB^/, ВВ^/ЕЕ^/, СС^/DD^/.Рёбра названных граней образуют контур собственной тени.

Все линии, ограничивающие сооружение, либо перпендикулярны, либо параллельны к плоскостям проекций.