Силовое взаимодействие потока с твердым телом, страница 2

N = Р_хu = рQ(v — u) u.  (4)

Из (4) следует, что передаваемая мощность зависит от скорости лопатки. Для нахождения скорости и, при которой будет макси­мальная мощность, находим экстремум функции N = f (u):

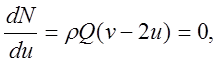
Откуда                           v = 2u.

Таким образом, максимальная передаваемая мощность и макси­мальный к. п. д. будут при и =2u. Оценим максимальный к. п. д. активной гидротурбины для теоретического случая (u = 1, ф = 1, Q = Q_T).

         Мощность струи

N_CTp = pgHQ = pQ (5)

Максимальная мощность, передаваемая плоским лопаткам,

Nmax = PQ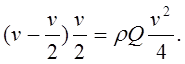 

Следовательно, теоретический максимальный к. п. д. активной турбины с плоскими лопатками будет

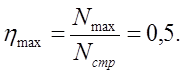
Чтобы повысить к. п. д., нужно применять лопатки профилиро­ванные, т. е. специальной формы. При ковшовых лопатках, оче­видно, к. п. д. будет выше.

Если струя вытекает из подвижного сосуда, то сила реакции заставит его двигаться в сторону, противоположную скорости потока. На этом принципе работают реактивные гидротурбины и двигатели.

В горной и строительной промышленности широко используется энергия водяной струи для разрушения и смыва горных пород и раз­личных материалов.

1.2.ОБТЕКАНИЕ ТЕЛ ЖИДКОСТЬЮ

Если твердое тело обтекается потоком жидкости или перемещается в пространстве, заполненном неподвижной жидкостью, то возникают гидроаэродинамические силы взаимодействия между телом и жидко­стью. В обоих этих случаях зависимости, опреде­ляющие величину силы, будут одни и те же, если одинаковы относительные скорости между телом и жидкостью. Важно здесь соблюдение законов подо­бия.

Рассмотрим свободное падение твердого тела в неограниченном объеме покоящейся жидкости (рис.4). Опущенное в жидкость тело начнет дви­гаться с ускорением  Уравнение движения:

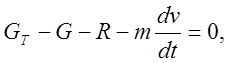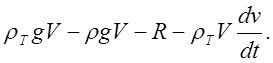 или (6)

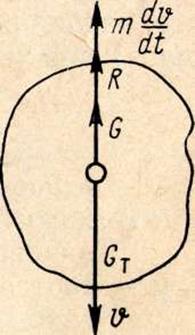
Рис.4 . Силы, ко­торые действуют на тело, пада­ющее в жидкости

Сила сопротивленияR определяется многими факторами. Но в основном зависит от скорости обтекания (v) в какой-то степени (m), т. е. R = кv^m, где к — коэффициент пропорциональности.

Тогда уравнение (6) можно представить:

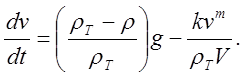                      (7)

Из (7) следует, что с увеличением скорости тела его ускорение уменьшается и при какой-то критической скорости v=vк dv/dt= 0. Эта скорость равномерного движения называется .скоростью свободного падения или гидравлической крупнос т ь ю, так как она наиболее полно характери­зует движение твердого тела в жидкости. _ч

Если поместить тело в вертикальный поток, дви­жущийся со скоростью v_к, то оно будет находиться в покое относительно не­подвижных границ потока (стенок труб и др.). По­этому эту скорость иногда называют скоростью в и т а н и я. При скоростях потока больших v_к тело будет уноситься вверх.

Режим обтекания жид­костью тела, а следова­тельно, и факторы, влия­ющие на силу могут быть различными. Основным определяющим критерием является число Рейнольдса:

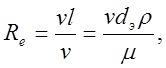
(8)

где v — относительная скорость обтекания,

l — характерный линейный размер, для частиц чаще всего эквивалентный (по объему шара) диаметр d_э = l; v,µ  — соответственно кинематический и динамический коэффици­енты вязкости жидкости.

Эксперименты показали, что для большинства частиц при Re << 1 режим обтекания ламинарный (рис.5, а). Например, этот режим будет в воде, еслиvd_э м²/сек. Следовательно, ламинарный режим возможен при обтекании тел с весьма малыми скоростями или при свободном падении мельчайших частиц (обычно d_э <1 мм). Этот режим представляет интерес при расчетах отстойников для осаждения ила, шлама и т. п.

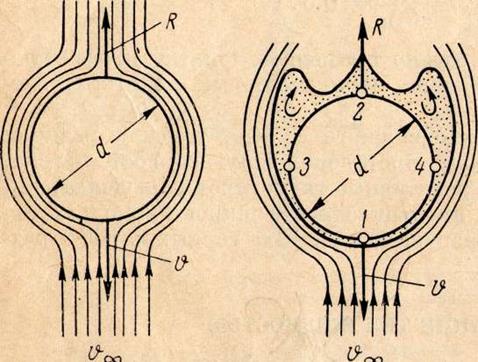  рис.5

Для этих условий Стоке получил формулу для силы сопротивле­ния:

R = (9)

Обтекание твердых тел при больших числах Рейнольдса проис­ходит с отрывом пограничного слоя, который, как и у труб, образуется вследствие вязкости жидкости. На (рис.4), б схе­матично представлена картина обтекания шарового профиля. Ско­рость частиц жидкости на линии тока, проходящей в бесконечности через центр шара, по мере приближения к нему уменьшается от v —  в бесконечности до нуля в точке 1. Закон распределения скоростей по поверхности профиля для невязкой жидкости — си­нусоидальный, т. е. в точках 3 и 4 скорость будет максимальной, а в точке 2, как и в точке 1, равной нулю. Вследствие этого по за­кону Бернулли соответствующим образом по профилю распреде­лится и давление: в точках 3 и 4 оно будет минимальным, а в точках 1 и 2 — максимальным.