Определение радиуса кривизны линзы R, входящей в устройство колец Ньютона, а также оценка доверительного интервала и относительной погрешности в определении величины R

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

« ИНСТИТУТ ЦВЕТНЫХ МЕТАЛЛОВ И ЗОЛОТА»СФУ

Кафедра физики

Лабораторная работа № 6

Определение радиуса кривизны  линзы

с помощью колец Ньютона

Выполнил:                                                                                  Проверил:

Красноярск 2010 г.

   Цель работы: Определение радиуса кривизны линзы  R,  входящей в устройство колец Ньютона, а также оценка доверительного интервала  и относительной погрешности в определении величины  R.

 Оборудование: Оптическая скамья, осветитель, диафрагма, прибор Ньютона,    линза-объектив, экран, светофильтр.

Теоретическое введение.

      Кольца Ньютона наблюдаются в случае соприкосновении выпуклой поверхности плоско-выпуклой линзы малой кривизны с плоско-параллельной поверхностью. Воздушная прослойка между плоскостью и линзой имеет переменную толщину, разность хода интерферирующих их лучей зависит от толщины этой прослойки.  Чем больше толщина воздушной прослойки, тем больше число наблюдаемых колец.

      Кольца Ньютона могут наблюдаться  в отраженном и проходящем свете.

     В отраженном  свете оптическая разность хода для колец Ньютона определяют, учитывая  λ/2,условием:

,

     В отраженном  свете по условию образовании максимума:

,

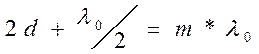     Для минимумов в отраженном свете:

.

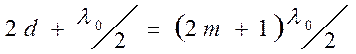      Так как на экране получаются увеличенные интерференционные кольца, то вначале надо рассчитать радиусы действительных колец:

,

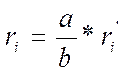Радиусы действительных колец рассчитывают для опыта с проходящим и отраженным светом. В первом случае берут радиусы колец определенного цвета, во втором – радиусы  темных  колец  при  условии,  что в опыте с отраженным  светом  использовали фильтр того же цвета.

      Радиус кривизны линзы, входящей в устройство колец Ньютона, определяется теоретически по формуле:

,

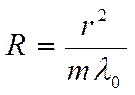     Так как практически трудно добиться идеального контакта сферической поверхности линзы и плоской пластинки в одной точке вследствие упругой деформации стекла и падения в место соприкосновения пылинки, то формулу использовать непосредственно нельзя: кольцу с номером m в действительности может соответствовать номер (m+p), где  p – неизвестное целое число, одинаковое для всех колец. Для исключения числа p  вычисление радиуса кривизны надо делать по разности квадратов радиуса двух колец:

.

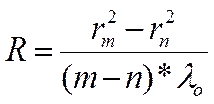Ход  работы:

     Измеряем  радиусы  полученных колец:

;  ; .

      Вычисляем радиусы действительных колец по формуле:

,

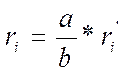где =155 мм=0,155 м; =445мм=0,445м.

;

;

;

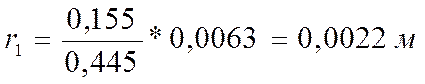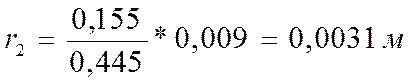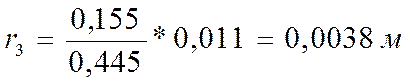    После того как мы вычислили действительные радиусы колец, вычисляем      радиус кривизны линзы по формуле:

,

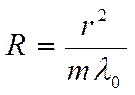Где =435 Нм=м,

;

;

.

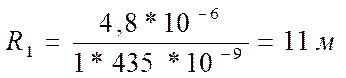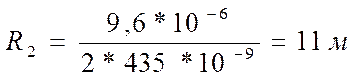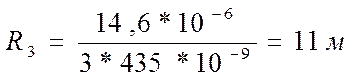Найдем среднее значение:

;

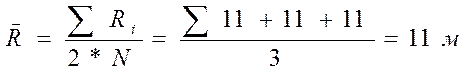Найдем средне квадратичную погрешность:

 ;

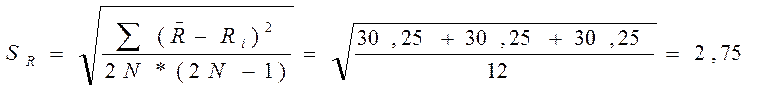Доверительный интервал найдем по формуле:

; ;

Найдем относительную погрешность:

.

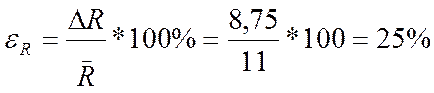Вывод:  Мы определили радиусы кривизны линзы  R,  входящей в устройство колец Ньютона, а также оценили доверительный интервал  и относительную погрешность в определении величины  R.