Трифазні електричні кола. Отримання трифазної системи ЕРС. Способи з’єднання фаз трифазного джерела. Поняття про лінійні і фазні напруги, страница 2

тому всі ці лінійні напруги можна подати так само, як і ЕРС в обмотці статора трифазного генератора: аналітично, графічно або за допомогою вектор­ної діаграми, зображеної на рис. 4.10.

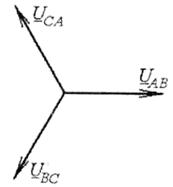
Рис. 4.10

3. Основні розрахункові співвідношення у трифазному навантаженні

Схема зірка (рис. 4.13)

Наведемо назви напруг і струмів, відображених на схемі:

U_А, U_в, U_с - фазні напруги в мережі – U_фм;

U_а, U_ь, U_с - фазні напруги на наванта­женні - U_фн;

І_А, І_в, І_с - лінійні струми – І_Ф;

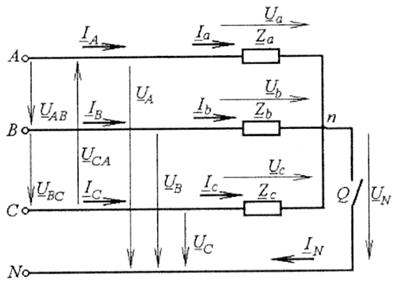
Рис. 4.13

І_а, І_b, І_с – фазні струми - І_ф;

І_N - струм нейтралі;

U_м - напруга змі­щення нейтралі.

При розрахунках трифазного наванта­ження звичайно вважається, що в мережі задана лінійна напруга U_л (U_АВ = U_ВС = U_СА = U_л), а також параметри кожної фази наван­таження, тобто повні опори Z_а, Z_ь, Z_с і фазові зсуви напруги і струму на них φ_а, φ_ь, φ_с.

У всіх варіантах для схеми «зірка» фазні напруги в мережі визначаються на основі отриманого раніше співвідношення (4.5):

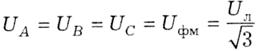
За наявності нейтрального проводу (вимикач Q на рис. 4.13 замкне­ний) на фазах приймача встановлюється така ж симетрична система фазних напруг, як і в мережі, тобто U_a = U_A; U_b = U_B; U_c = U_c (викорис­товуючи векторне зображення, маємо на увазі рівність відповідних напруг за величиною і фазою) або для діючих значень U_фн= U_фм.

За відсутності нейтрального проводу (вимикач Q на рис. 4.13 розімкнутий) ситуація рівності відповідних фазних напруг U_a = U_A; U_b ⁼ U_в; U_c = U_c або U_фн⁼ U_фм забезпечується тільки при симет­ричному навантаженні.

Для вказаних ситуацій при U_фп=U_фш розрахунок має такий порядок.

За законом Ома визначаються фазні струми:

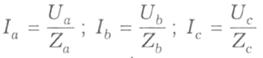
При симетричному навантаженні, з урахуванням рівності опорів фаз Z_a - Z_b = Z_c = Z_ф і фазних напруг U_a = U_b = U_c = U_фн, отри­муємо однакові фазні струми І_ф = І_а=І_ь = І_с, при несиметричному навантаженні – різні струми.

За схемою «зірка» (див. рис. 4.13) лінійні і фазні струми дорів­нюють один одному: І_А = І_а; І_в = І_ь; І_с = І_с або І_л = І_ф.

Якщо є нейтральний провід, то на основі першого закону Кірхгофа струм у ньому:

I_N=I+I_b+I_c.

Це підсумовування стосується векторної форми струмів, тому скористаємося векторною діаграмою.

На рис. 4.14 ілюстрація відповідає симетричному навантаженню: спочатку будуємо симетричну систему фазних напруг, а потім однакові за довжиною вектори фазних струмів, кожний із яких проводимо під кутом φ_ф по відношенню до своєї фазної напруги (фазовий зсув при симетричному навантаженні скрізь однаковий: φ_а = φ_ь = φ_с - φ_ф). Для прикладу припустимо активно-індуктивний характер навантаження, тобто φ_ф>0. Підсумовування за формулою (4.10) при симетрич­ному навантаженні дає струм нейтралі, який дорівнює нулю. Отже, при симетричному навантаженні нейтральний провід не потрібен.

На рис. 4.15 ілюстрація відповідає несиметричному навантаженню: знову спочатку будуємо симетричну систему фазних напруг, а потім різні за довжиною вектори фазних струмів, кожний із яких проводимо під своїм кутом φ_а, φ_ь, φ_с по відношенню до своєї фазної напруги. Для прикладу при­пустимо φ_а>0, φ_ь = 0, φ_с<0.

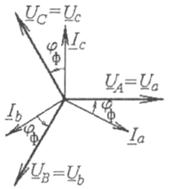
Рис. 4.14

Підсумовування за формулою (4.10) дає струм нейтралі, який при несиметричному навантаженні не дорівнює нулю.

Розрахунковим шляхом струм нейтралі можна визначити за тією ж формулою (4.10), але проводячи попередньо обчислювання фазних струмів символічним методом

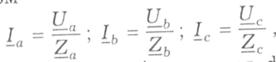
де використовуються комплексні значення фазних напруг на навантаженні U_а = U_фн; U_ь = U_фне^j120°; U_с = U_фне^j120° і опорів фаз Z_a, Z_b, Z_c.

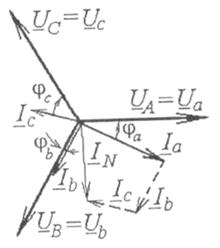
Рис. 4.15

Якщо при несиметричному навантаженні відбудеться обрив нейтрального проводу, то з'являється напруга «зміщення ней­тралі» U_N , яка може бути обчислена символічним методом:

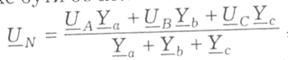
де комплексні значення фазних напруг у мережі U_A = U_ФМ; U_ь = U_фне^j120°; U_с = U_фне^j120° і провідностей фаз ; ; .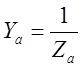

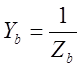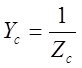Тоді фазні напруги на приймачах на підставі другого закону Кірхгофа за рис. 4.13:

Ці напруги будуть різними: виникає так званий «перекіс фаз», який ілюструється за допомогою векторної діаграми на рис. 4.16. Тобто фазні напруги на навантаженні відріз­няються одна від одної і від фазних напруг у мережі, що недопустимо.

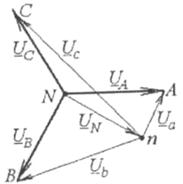
Рис. 4.16

Активну потужність у всіх випадках можна розраховувати для кожної з фаз приймача:

Р_а = U_aI_acosφ_a; Р_ь = U_bI_bcosφ_b; Р_с = U_cI_ccosφ_c,

а для всієї «зірки»:

Р_Y = Р_а+Р_b+Р_с.

При симетричному навантаженні активну потужність можна розрахувати для однієї фази:

P_ф = U_фI_фcosφ_ф,

тоді для всієї зірки P_Y = 3Р_ф.

При симетричному навантаженні з урахуванням того, що I_ф = І_л і U_фн = Uл/, отримаємо вираз потужності через лінійні величини:

Аналогічно для кола за схемою «зірка» розраховуються реак­тивні потужності

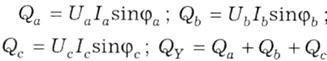
а при симетричному навантаженні:

Схема трикутник (рис. 4.17)

Наведемо назви напруг і струмів, відображених на схемі Δ: .U_АВ, U_BC, U_CA - лінійні напруги U_M, причому при з'єднанні три­кутником вони безпосередньо утворюють і фазні напруги U_ф на навантаженні U_ab, U_bc, U_ca;