Приклад комплексного методу розрахунку ланцюгів змінного струму

Файл 2

Приклад комплексного методу розрахунку ланцюгів змінного струму

    Комплексний метод дозволяє записати вектор кожної електричної величини комплексним числом і всі геометричні операції над векторами замінити алгебраїчними діями над комплексними числами.

1. Вектор і комплексне число

     Вектор і комплексне число – два взаємозалежних поняття.

     Комплексне число можна наочно представити на площині (Рис. 1). Йому відповідає точка, положення якої однозначно визначають матеріальна a і мінімальна b складові проекції вектора A на матеріальна і мнимі осі. Комплексне число в алгебраїчній формі*

             Ā= а + jb,                                                                                                                            (1)

де j = .

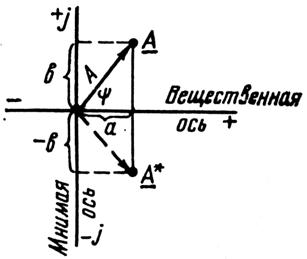
Рис. 1 Вектор на комплексній величині.

            Це ж комплексне число можна записати в тригонометричній формі. Тому що а = А cosψ, а b = А sinψ, де

А= - довжина вектора , то Ā= А cosψ +jАsinψ = А(cosψ +jsinψ ).

     Число А називається модулем, кут ψ- аргументом комплексного числа. Застосувавши відому з математики формулу Эйлера  

cosψ +jsinψ  = е^+jψ ,              (2)

те ж комплексне число запишемо в показовій формі:

                                                                       Ā= А е^+jψ .                    (3)

     Надалі нам знадобитися «сполучене комплексне число». Так називають комплексне число, якому геометрично відповідає дзеркальне відображення точки щодо речовинної осі. З Рис. 1 випливає, що Ā*= а – jb=А е^-jψ.

2. Основні операції над вектором

     Додавання і віднімання векторів. Воно зводиться до алгебраїчного додавання (віднімання) комплексних чисел, для чого алгебраїчно складають або віднімають окремо їх матеріальні або мнимі частини: Ā₁=  а₁ + jb₁; Ā₂=а₂ + jb₂; Ā=Ā₁+Ā₂=(а₁ а₂)+j(b₁ b₂).

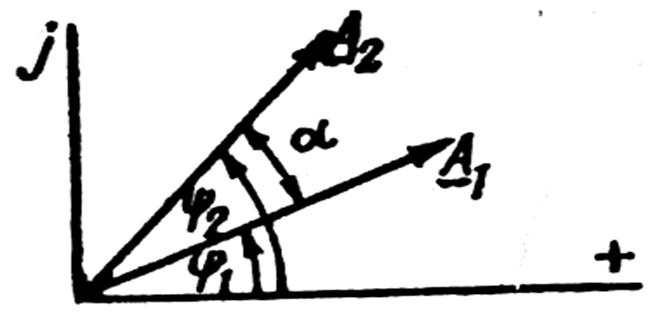
Рис. 2. Поворот вектора на кут

Множення і ділення векторів. Комплексні числа, що відповідають векторам, записуємо в показовій формі: Ā₁=  А₁ е^+jψ; Ā₂=A₂ е^+jψ. Потім модулі перемножуємо і модулі додаємо  Ā₁Ā₂=А₁A₂е^j(ψ+ψ ).

     Щоб записати частку, треба розділити модулі і відняти аргументи: Ā₁/Ā₂=А₁ е^+jψ/A₂ е^+jψ=(А₁/A₂)е^j(ψ-ψ ).

     Поворот вектора. На комплексній площині (2) побудовані два вектори однакової довжини, тобто з рівними модулями А. Аргументи векторів ψ₁, ψ₂ різні. Комплексні числа в показовій формі відповідають цим векторам: Ā₁=  А₁ е^+jψ; Ā₂=A₂ е^+jψ. З Рис.2  ψ=ψ+α; тоді Ā₂=A е^+j(ψ+α)=А е^+jψ е^+jα=А₁ е^jα.

     Щоб повернути вектор на кут α у напрямку від матеріальної до мініРисьної осі, тобто проти руху годинникової стрілки (цей напрямок будемо вважати позитивним), треба його комплексне число помножити на е^jα.

     Якщо α=π/2, то по формулі Ейлера (2) е^jπ/2= cosπ/2+jsinπ/2=0+j і Ā₂=  Ā₁е^jπ/2 = j₁, тобто множення комплексного числа на j відповідає повороту вектора на +90^°. Подібним чином множенню вектора на –j відповідає його поворот на -90°. Множення комплексного числа на( j)² =-1 повертає вектор на 180°. Множник е^jα= cosα+jsinα називають оператором повороту вектора.

     Обертання вектора. Вектор, що обертається в позитивному напрямку з постійною кутовою швидкістю ω, записують комплексним числом, аргумент якого лінійно зростає згодом: = Aе^j(ψ+ωt)=Aе^jψе^jωt, де ψ- початкове значення аргументу (при t = 0).

3. Формули для розрахунку ланцюга змінного струму в комплексній формі

     Струм, напруга і эдс у комплексній формі. Синусоїдальний змінний струм з діючим значенням I ми ще раніш умовилися зображувати обертовим радіусом-вектором.

     У показовій формі обертовий вектор можна записати комплексним числом

Iе^jψ е^jωt,

де ψ- початкова фаза струму (тобто положення вектора в момент початку відліку, t=0);

      ωt – аргумент або фазовий кут.

     Векторну діаграму ми завжди розглядаємо як нерухому, тому множник е^jωt можна опустити.

     Вираз =I^jψ називають комплексним струмом. Аналогічно записують комплексну напругу =U е^jψ і =е^jψ . Відношення до називають комплексним опором і позначають    :

= / =(U/I)е^jψ /е^jψ .                                                                                                                                                                                         (5)