Кола синусоїдного струму. Отримання синусоїдних електричних величин. Форми зображення синусоїдних величин. Співвідношення напруги і струму на ідеальних елементах схем заміщення

Лекція 3

Тема: Кола синусоїдного струму

План лекції

1. Отримання синусоїдних електричних величин.

2. Форми зображення синусоїдних величин.

3. Співвідношення напруги і струму на ідеальних елементах схем заміщення.

1. Отримання синусоїдних електричних величин

Колами синусоїдного струму називаються такі електричні кола, в яких часові функції електричних величин, тобто електрорушійні сили (ЕРС), напруги та струми, змінюються за гармоніч­ним - синусоїдним - законом. Знайомство з такими колами починається з однофазних кіл. В однофазному колі діє одне синусоїдне джерело ЕРС або воно живиться від двопровідного джерела синусоїдної напруги.

Основою кіл синусоїдного струму є генератори змінного струму, в яких виробляються синусоїдні ЕРС. Тому, перш ніж вивчати процеси в цих колах, розглянемо принцип отримання ЕРС, яка змінюється в часі за синусоїдним законом.

На рис. 3.1, а зображено простіший однофазний генератор, який виробляє синусоїдну ЕРС. Тут прямокутна провідникова рамка abed (виток) обертається з кутовою швидкістю Q між полюсами N і S постійного магніту, який збуджує магнітне поле. При цьому, згідно із законом електромагнітної індукції, у повздовжних частинах рамки ab і cd індукуються ЕРС е_аb і e_cd, напрямки яких установлюються за правилом «правої руки».

Визначимо вказані ЕРС, вико­ристовуючи поперечний переріз моделі генератора за рис. 3.1,6. Тут зазначені лінійні швидкості пере­міщення боків рамки V, а також показані напрямки силових ліній магнітного поля і, відповідно, напрямок вектора магнітної індукції В. ЕРС у провіднику рамки ab складає:

e_ab = BVlsinα,

де І - довжина боку рамки; α - кут між векторами V і В.

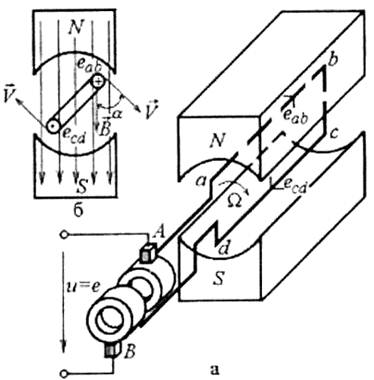
Рис. 3.1

Вважатимемо, що магнітне поле однорідне, тобто в зоні обер­тання рамки магнітна індукція скрізь однакова за величиною і напрямком. Тоді у формулі (3.1) змінюється тільки кут а (через безперервну зміну напрямку вектора швидкості), який визнача­ється так: α = Ωt.

У другому боці рамки ЕРС е_сй аналогічна, але має протилеж­ний напрямок. Однак, якщо робити обхід за контуром рамки, то ЕРС її двох боків додаються, і на всю рамку отримуємо ЕРС:

е = е_аb +е_cd = 2е_ab = 2ВVlsin = 2ВVIsinΩt

У цій формулі позначимо Е_т=2ВVІ, і це є не що інше, як амп­літуда ЕРС. Таким чином у контурі отримуємо синусоїдну ЕРС:

е = Е_тsinΩt.

Через контактні кільця, що обертаються разом із рамкою, і через нерухомі щітки А і В, що ковзають по поверхні контактних кілець, ЕРС передається на вихідні затискачі генератора, утворю­ючи на них відповідну синусоїдну напругу и, яка дорівнює е (див. рис. 3.1, а). Якщо до затискачів на щітках під'єднати будь-яке електричне навантаження, то в електричному колі, що утвориться, виникне синусоїдний струм.

Конструкція реальних генераторів значно складніша, і в них замість рамки використовують багатовиткову обмотку. Тоді амплі­туда ЕРС зростає пропорційно кількості витків. Однак принцип дії таких генераторів відповідає тому, який розглядається на рис. 3.1.

2. Форми зображення синусоїдних електричних величин

При аналізі процесів у колах синусоїдного струму можливе використання різних форм зображення синусоїдних електричних величин. Наведемо ці форми для напруги, струму і ЕРС.

1. Аналітична форма

де u, і, е - миттєві значення; U_т , І_т ,Е_т - амплітуди; ω – кутова частота [с^-1], яка замінила кутову швидкість Ω в, бо це не завжди одне й те ж:

причому 1/Т = f -  частота [Гц], Т - період повторення [с]; ψ_u, ψ_i, ψ_e - початкові фази.

Наприклад, при f=50 Гц маємо ω=314 с¹, Т=0,02 с.

При порівнянні напруги і струму за часом використовують різ­ницю часових фаз, вводячи поняття фазовий зсув

причому тут первісно напругу поставлено на перше місце, а струм - на друге, що зумовлює в подальшому знаки («+» або «-») у низці формул і в інших випадках.

Можливі такі комбінації і відповідна термінологія: ψ_u ≥ ψ_i напруга за фазою випереджає струм: φ>0; ψ_u=ψ_i - напруга і струм збігаються за фазою: φ=0; ψ_u<ψ_i - напруга відстає за фазою від струму: φ<0.

2. Графічна форма. Синусоїди напруги u і струму і подані на рис. 3.2, причому рису­нок відповідає значен­ням величин ψ_u>0; ψ_i<0; φ>0. Замість часу і по осі абсцис прийнято відкла­дати ωt: так переходять від секунд до радіанів. Це зручно, тому що так легко встановити масш­таб по цій осі (період синусоїд дорівнює 2π).

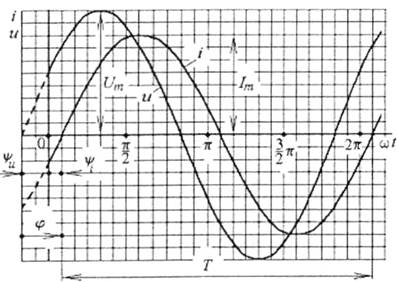
Рис. 3.2

3. Діюче значення. Вихідна формула (1.37) і зміст діючого значення струму вже були подані раніше, а далі для конкретного виразу синусоїдного струму і = I_тsinωt проводимо необхідні перетворення:

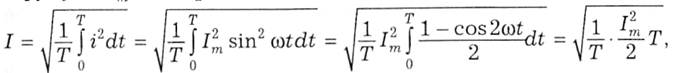
із цього  вже отримаємо діюче значення синусоїдного струму:

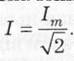
Аналогічно для синусоїдних напруги і ЕРС отримуємо діючі значення за формулами:

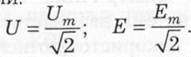
Зазначимо, що в колах синусоїдного струму при вимірюван­нях та розрахунках прийнято оперувати діючими значеннями електричних величин.

4. Середнє значення. За період Т маємо середнє значення

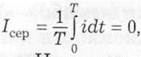
що характерно для будь-якої синусоїди.

На практиці прийнято брати середнє значення за півперіоду:

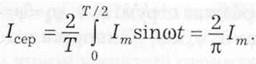
Аналогічно для напруги

5. Векторне зображення. Із курсу математики відомо, що синусоїди можна зобразити векторами, що обертаються з кутовою швидкістю ω проти руху годинникової стрілки, а їхні довжини дорівнюють амп­літудам U_т, І_т у відповідних масштабах. Так, синусоїдні напруга і струм у вигляді обертових векторів показані на рис. 3.3,а. Якщо визначити проекцію вектора на вісь ординат, як це показано для напруги, то отримуємо безпосередньо синусоїду цієї електрич­ної величини U = U_тsin(ωt + ψ_и), що повторює (3.4).

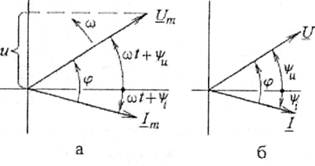
Рис. 3.3

На практиці прийнято зображати вектори для фіксованого моменту часу t=0, а довжини векторів брати в масштабі рівними діючому значенню (3.7), (3.8) відповідної електричної величини (рис. 3.3,6). Тоді вектори займають положення по відношенню до горизонтальної осі під кутами, що дорівнюють початковим фазам електричних величин. Кут зсуву фаз φ відкладають від вектора струму до вектора напруги, що належить далі завжди враховувати, визначаючи знак цього кута.

Прийнято, що позитивні кути відкладаються проти руху годин­никової стрілки.

Сукупність векторів електричних величин, зображених у спільній координатній системі, називається векторною діагра­мою. Векторні діаграми використовуються при виводі основних розрахункових співвідношень для кіл синусоїдного струму при розв'язанні задач, для перевірки результатів розв'язання тощо.