Кола синусоїдного струму. Отримання синусоїдних електричних величин. Форми зображення синусоїдних величин. Співвідношення напруги і струму на ідеальних елементах схем заміщення, страница 2

У відповідності з векторним зображенням синусоїд, закони Кірхгофа,) для кіл синусоїдного струму набувають модифікації:

перший закон Кірхгофа:

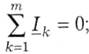
другий закон Кірхгофа:

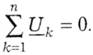
Тут додаються вектори діючих значень. Усі правила складання рівнянь і урахування знаків зберігаються, тільки тепер ідеться про геометричні суми векторів. Довжини векторів дорівнюють діючим значенням, тому їхні літерні позначення однакові. А щоб не плутати вектори та діючі значення, позначення перших під­креслюють.

6. Зображення за допомогою комплексних чисел. Вектори електричних величин розміщуються на площині комплексних чисел (рис. 3.4) з осями дійсних (-1;+1) і уявних (-j; +j) чисел, де j=1 - уявна одиниця (у математиці вона познача­лася літерою і, але у даному разі це струм).

Ці величини, наприклад, напругу і струм, можна зобразити:

а) в алгебраїчній формі:

де U',I’ - дійсні, U", І" - уявні складові комп­лексних величин у показовій формі:

де U, І - модулі, що дорівнюють діючим значенням відповідних величин; ψ_u, ψ_i - аргументи, що дорівнюють початковим фазам; е - основа натуральних лога­рифмів (не плутати з ЕРС).

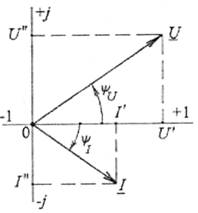
Рис. 3.4

Перехід із однієї форми в іншу виконується за відомими пра­вилами, наприклад, для напруги:

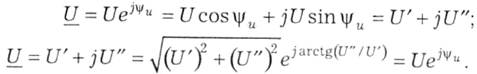
Закони Кірхгофа при використанні комплексної форми величин отримують модифікацію, яка зовні збігається з виразами (3.10) і (3.11) у разі використання векторного зображення синусо­їдних електричних величин, однак тепер в формули і рівняння повинні підставляться комплексні величини:

перший закон Кірхгофа:

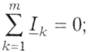
другий закон Кірхгофа:

3. Співвідношення напруги і струму на ідеальних елементах схем заміщення

Для розрахунку кіл синусоїдного струму основоположними є співвідношення напруги і струму на пасивних ідеальних елемен­тах R, L і С. Причому, на відміну від кіл постійного струму, важли­вим є співвідношення напруги та струму не тільки за значенням, але і за часом, тобто фазовий зсув між ними.

Виведемо та проілюструємо ці співвідношення. Розглядаючи конкретний ідеальний елемент, будемо вважати заданим синусоїд­ний струм і параметр цього елемента (R або L, або С). А задача буде полягати у визначенні часової функції напруги, а потім і вка­заних кількісних і часових співвідношень.

1. Ідеальний резистивний елемент R (рис. 3.8, а).

Задано, що по ділянці кола з цим елементом R проходить струм і=І_т sin(ωt+ψ_i); належить визначити функцію напруги u_R(t).

Використовуючи загальний вираз (1.4) для змінних струму і напруги, маємо:

Звідси амплітуда напруги U_т = RI_т, що є законом Ома для амплітуд. А якщо врахувати,  І_т=2І, U_т =2U, то отримуємо закон Ома для діючих значень напруги і струму на ідеальному резистивному елементі:

Кутова частота напруги со зберігається такою, як і у струму. Початкова фаза напруги у (3.18) збігається із початковою фазою струму: ψ_u = ψ_i; тоді за (3.6) фазовий зсув:

φ_R = 0

На рис. 3.8, б показані синусоїди струму і напруги, на рис. 3.8, в - їхнє векторне зображення. Очевидно, що якщо початкова фаза струму задана і побудована синусоїда струму або його вектор, то напруга збігається за фазою зі струмом.