Розв’язок
1. Визначаємо струми у вітках:
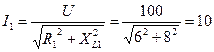
2. Кути здвигу фаз у вітках знаходимо по синусам кутів, щоб запобігти втрати знаку кута:
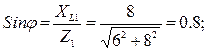 φ=53010
φ=53010
Через те, що φ> 0, то напруга випереджує струм, sinφ2= - ХС2/Z2 = = -10/10 == -1,0; φ2 = -90° - напруга відстає від струму, тому що φ2< 0. За таблицями Брадіса знаходимо соs φ2 = соs 53°10'=0,6; соs φ2= 0.
3. Визначаємо активні та реактивні складові струмів у гілках:
Ia1=I1cos φ1=10*0.6=6A; IP1=I1sin φ1=10*0.8=8A;
Ia2=0A; IP1=10*(-1)=-10A;
4. Визначаємо струм в нерозгалуженій частині ланцюга:
![]()
5. Визначаємо коефіцієнт потужності всього ланцюга:
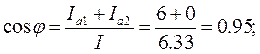
6. Визначаємо активні та реактивні потужності гілок та всього ланцюга:
P1=U I1 cosφ1 =100*10*0.6 =600 Вт;
P2=0; P=P1+P2=6ООВт;
Q1=U I1 sinφ1 =100*10*0.8 =800Вар;
Q2=U I2 sinφ2 =100*10*(-1) =- 1000 Вар;
Q=Q1+Q2= 800 — 1000 = — 200 Вар.
Увага! Реактивна потужність гілки з ємкістю зі знаком «мінус», тому що φ< 0.
7. Визначаємо повну потужність ланцюга:
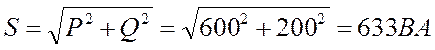
Струм у нерозгалуженій частиш кола можна визначити значно простіше,
без розкладів струмів на складові, знаючи повну потужність кола та напругу:
I=S/U=633/100 ==6,33 А,
8. Для побудови векторної діаграми задаємося масштабом по струму: в 1 см -2,5 А та масштабом по напрузі: в 1 см - 25В. Побудову починаємо з вектора напруги U (Рис. 4, б). Під кутом φ1 до нього (в бік відставання) відкладаємо в масштабі вектор току її, під кутом φ2 (в сторону випередження) – вектор струму І2. Геометрична сума цих струмів дорівнює струму в нерозгалуженій частині ланцюга. На діаграмі показані також проекція векторів струмів на вектор напруги (активна складова Іа1) та вектор, перпендикулярний до нього (реактивні складові Ір1 та Ір2). При відсутності конденсатора реактивна потужність першої вітки не компенсувалася б і струм в ланцюзі збільшувався б до І=І1=10А.
Методичні вказівки до розв’язку задач 5-6
Розв’язок задач цієї групи потребує знання учбового матеріалу теми, чіткого уявлення про особливості з'єднання джерела та споживачів в зірку та трикутник, співвідношення між лінійними та фазними величинами при таких з'єднаннях, а також уміння будувати векторні діаграми при симетричній та несиметричній навантаженнях. Зміст задач та схеми ланцюгів наведені в умовах завдань, а дані до них у відповідних таблицях. Для пояснення загальної методики розв'язання задач на трифазні ланцюги, включаючи побудову векторних діаграм, розглянуті типові приклади 5-10.
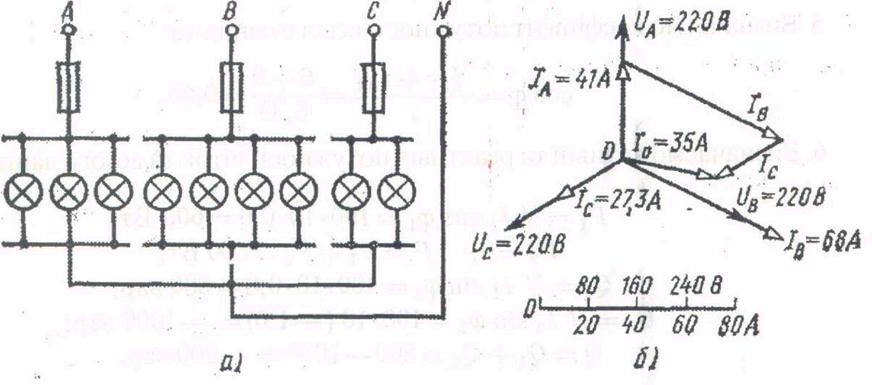
Рис.5
Приклад 5. У трифазну чотириповідну мережу ввімкнені зіркою лампи освітлення потужністю Р = 300 Вт кожна. У фазу А ввімкнули 30 ламп, у фазу В - 50 ламп та у фазу С- 20 ламп. Лінійна напруга мережі Uном = 380В (Рис. 5, а). Визначити струми в фазах та накреслити векторну діаграму ланцюга, з якої знайти числове значення струму в нульовому проводі.
Розв’язок.
Визначаємо фазні напруги установки:
UA=UB=UC=UHOM/√3=380/1.73= 220 В,
2. Знаходимо фазні струми:
IA=PФА/UA=300*30/220=41A; IC=PФC/UC=300*20/220=27.3A;
IB=PФB/UB=300*50/220=68A;
3. Для побудови векторної діаграми обираємо масштаби по струму:
1 см - 20 А та по напрузі: 1 см - 80 В. Побудову діаграми починаємо з векторів фазних напруг UA, Uв, Uс (Рис. 5, б), розташовуючи їх під кутом 120 друг відповідно друга. Чергування фаз звичайне: за фазою А - фаза В, за фазою В - фаза С. Лампи освітлення є активним навантаженням, через це струм у кожній фазі збігається з відповідною фазною напругою. У фазі А струм Iа = 41 А, через це на діаграмі він буде мати вигляд вектора, довжина якого дорівнює 41/20=2,05 см. Довжина вектора фазної напруги UA складе 220/80=2,75 см. По тому ж принципу будуємо вектори струмів та напруг в інших фазах. Струм Іо в нульовому проводі є геометричною сумою всіх фазних струмів. Вимірюючи довжину вектора струму Іо в нульовому проводі, отримуємо 1,75 см, через це I0= 1,75х20=35А. Вектори лінійних напруг на діаграмі не вказані, щоб не ускладнювати креслення.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.