




ПРИКЛАДИ РОЗВ’ЯЗАННЯ ТИПОВИХ ЗАВДАНЬ
ДЛЯ САМОСТІЙНОЇ РОБОТИ СТУДЕНТІВ
З дисципліни: «Математико-статистичні методи досліджень».
(9 семестр)
Задача 1.
Відома врожайність в центнерах з гектара озимої пшениці по 25 КСП: 29,4; 24,8; 44,1;22,6; 40,3; 26,6; 32,4; 33,1; 25,7; 37,2; 31,4; 34,4; 38,2; 44,5; 42,8; 39,3; 28,8; 20,5; 36,3; 27,5; 30,6;29,3; 24,1; 23,6; 39,8. Побудувати ранжувальний ряд, інтервальний варіаційний ряд, полігон, гістограму відносних частот, вибіркову функцію розподілу і її графік.
Розв’язання. Для побудови ранжувального ряду запишемо наведені результати врожайності в порядку зростання: 20,5; 22,6; 23,6; 24,1; 24,8; 25,7; 26,6; 27,5; 28,8; 29,3; 29,4; 30,6; 31,4; 32,4; 33,1; 34,4; 36,3; 37,2; 38,2; 39,3; 39,8; 40,3; 42,8; 44,1; 44,5.
Для побудови варіаційного інтервального ряду визначимо число інтервалів:
![]()
Величину (довжину) інтервалу визначимо за формулою
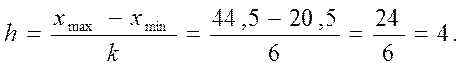
Визначимо межі інтервалів, представників інтервалів, як середнє
арифметичне меж інтервалів, частоти інтервалів ![]() ,
відносні частоти
,
відносні частоти 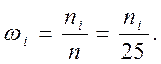 Одержані результати
занесемо до таблиці, яку називають варіаційним інтервальним рядом досліджуваної
випадкової величини.
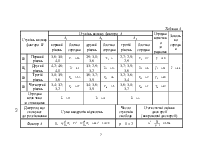
Одержані результати
занесемо до таблиці, яку називають варіаційним інтервальним рядом досліджуваної
випадкової величини.
|
Інтервали |
|
|
|
|
|
|
|
|
22,5 |
26,5 |
30,5 |
34,5 |
38,5 |
42,5 |
|
|
4 |
4 |
6 |
3 |
5 |
3 |
|
|
|
|
|
|
|
|
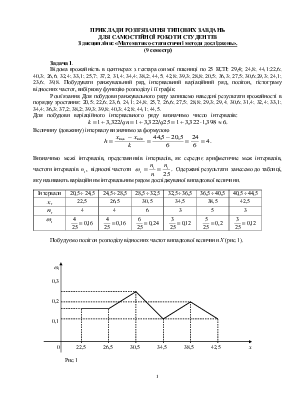
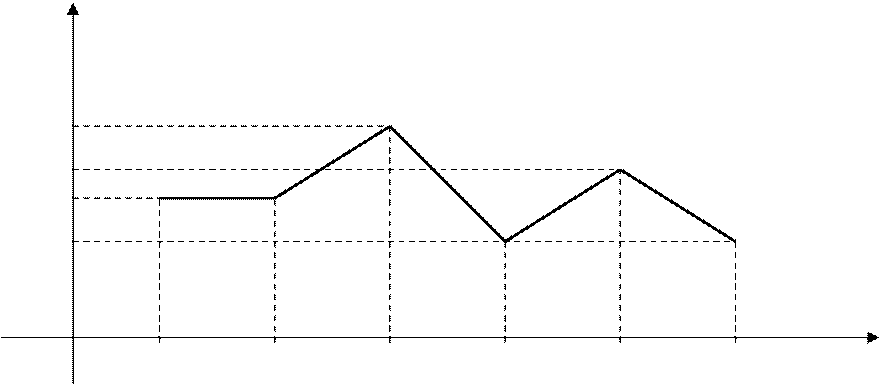
Побудуємо полігон розподілу відносних частот випадкової величини Х (рис.1).
 |
![]()
0,3
0,2
0,1
0 22,5 26,5 30,5 34,5 38,5 42,5 х
Рис.1
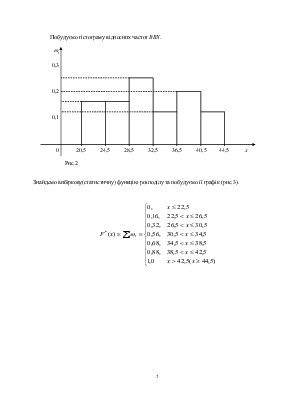
Побудуємо гістограму відносних частот ВВХ.
![]()
![]()
0,3
 |
![]()
![]()
![]()
![]() 0,2
0,2
 |
|||
 |
0,1
0 20,5 24,5 28,5 32,5 36,5 40,5 44,5 x
Рис.2
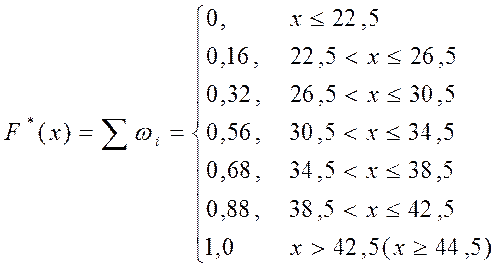
![]()
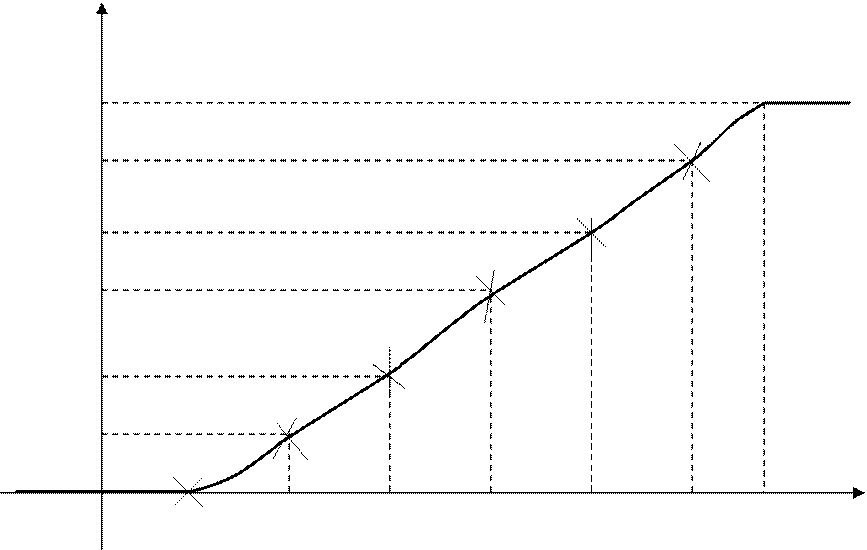
![]()
1,0
0,88
0,68
0,56
0,32
0,16
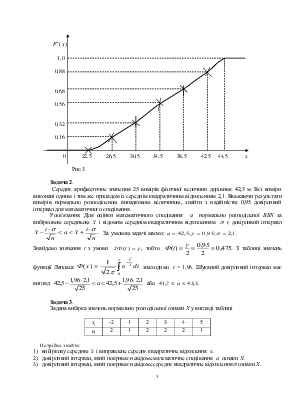
0 22,5 26,5 30,5 34,5 38,5 42,5 44,5 х
Рис.3
Задача 2.
Середнє арифметичне значення 25 вимірів фізичної величини дорівнює 42,5 м. Всі виміри виконані одним і тим же приладом із середнім квадратичним відхиленням 2,1. Вважаючи результати вимірів нормально розподіленою випадковою величиною, знайти з надійністю 0,95 довірливий інтервал для математичного сподівання.
Розв’язання. Для оцінки математичного сподівання а
нормально розподіленої ВВХ за вибірковою середньою ![]() і відомим середнім квадратичним
відхиленням
і відомим середнім квадратичним
відхиленням ![]() є довірливий інтервал
є довірливий інтервал 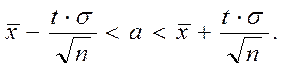 За умовою задачі маємо:
За умовою задачі маємо: ![]()
Знайдемо значення tз умови ![]() тобто
тобто 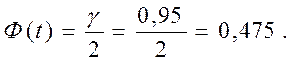 З таблиці значень функції Лапласа
З таблиці значень функції Лапласа 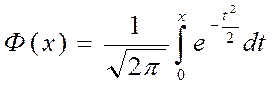 знаходимо t
= 1,96. Шуканий довірливий
інтервал має вигляд
знаходимо t
= 1,96. Шуканий довірливий
інтервал має вигляд 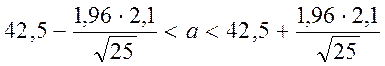 або
або ![]()
Задача 3.
Задана вибірка значень нормально розподіленої ознаки Х у вигляді таблиці
|
|
-2 |
1 |
2 |
3 |
4 |
5 |
||
|
|
2 |
1 |
2 |
2 |
2 |
1 |
Потрібно знайти:
1)
вибіркову середню ![]() і виправлене середнє квадратичне
відхилення s;
і виправлене середнє квадратичне
відхилення s;
2) довірливий інтервал, який покриває невідоме математичне сподівання а ознаки Х;
3)
довірливий інтервал, який
покриває невідоме середнє квадратичне відхилення![]() ознаки
Х.
ознаки
Х.
Надійність оцінки ![]()
Розв’язання
1.
Знайдемо об’єм вибірки 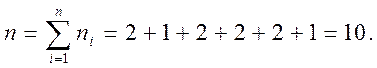 Знайдемо
вибіркову
Знайдемо
вибіркову
середню ![]() за формулою
за формулою 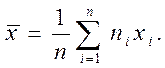 Підставляючи числові
значення, знайдемо
Підставляючи числові
значення, знайдемо
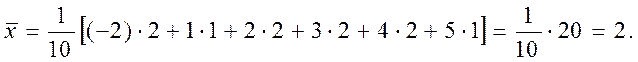
Обчислимо спочатку виправлену вибіркову дисперсію
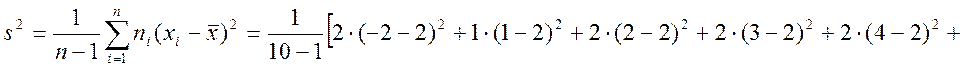
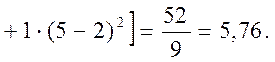 Отже, виправлене середнє квадратичне відхилення
Отже, виправлене середнє квадратичне відхилення
![]()
2. Довірливий інтервал для невідомого математичного сподівання має вигляд
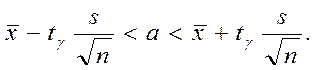
За таблицею значень ![]() (додаток №3) при n
= 10,
(додаток №3) при n
= 10, ![]() знаходимо
знаходимо ![]() Послідовно обчислюємо:
Послідовно обчислюємо: 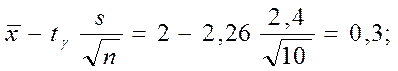
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.