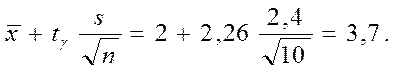
Отже, шуканий інтервал має вигляд 0,3 < a < 3,7.
3. Довірливий інтервал для генерального середнього квадратичного
відхилення ![]() знайдемо за однією з формул:
знайдемо за однією з формул: ![]() , якщо q< 1;
, якщо q< 1; ![]() , якщо
, якщо ![]() Відповідне
значення q знайдемо за таблицею значень
Відповідне
значення q знайдемо за таблицею значень ![]() При
При ![]() ,
n=
10 маємо q
= 0,65. Таким чином, довірливий інтервал має вигляд
,
n=
10 маємо q
= 0,65. Таким чином, довірливий інтервал має вигляд
![]() або
або ![]()
Задача 4.
Реалізувавши вибірку з генеральної сукупності, ознака якої Х має нормальний закон розподілу, дістали статистичний розподіл:
|
xi |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
ni |
1 |
3 |
6 |
8 |
6 |
6 |
5 |
3 |
2 |
При рівні значущості a = 0,01 перевірити правильність нульової гіпотези
![]() , якщо
альтернативна гіпотеза
, якщо
альтернативна гіпотеза ![]() .
.
Розв’язання. Обчислимо значення ![]() :
:
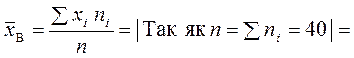
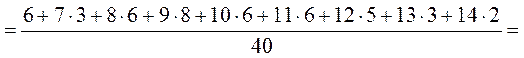
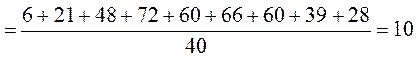 .
.
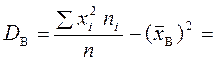
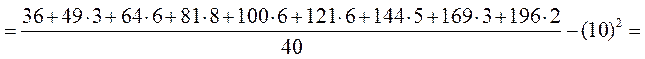
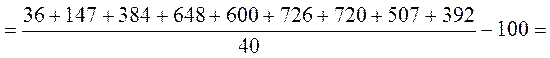
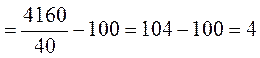 .
.
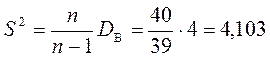 .
.
![]() .
.
При альтернативній гіпотезі ![]() будуємо двобічну критичну область.
Враховуючи, що sГ є невідомою величиною, для побудови цієї області беремо статистичний
критерій.
будуємо двобічну критичну область.
Враховуючи, що sГ є невідомою величиною, для побудови цієї області беремо статистичний
критерій.
Оскільки критичні точки ![]() і
і ![]() симетричні
відносно нуля і при цьому
симетричні
відносно нуля і при цьому ![]() = –
= – ![]() , знаходимо за таблицею
(додаток 6)
, знаходимо за таблицею
(додаток 6) ![]() :
:
![]() .
.
Тоді ![]() =
– 2,7.
=
– 2,7.
Двобічна критична область зображена на рис. 1.
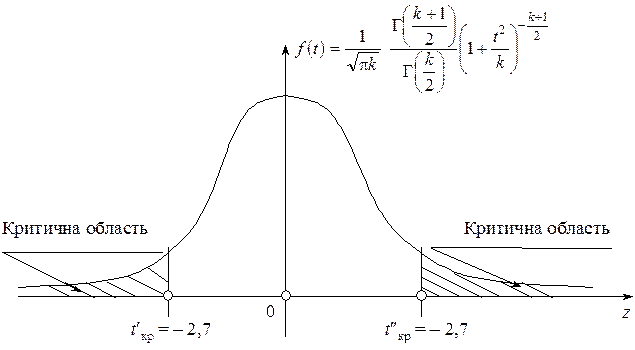
Рис. 1
Обчислимо спостережуване значення критерію:
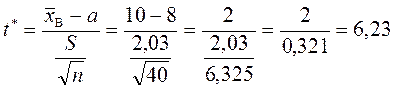 .
.
Висновок. Оскільки ![]() , то немає
підстав приймати
, то немає
підстав приймати ![]() .
.
Задача 5. Елементи дисперсійного аналізу
У чотирьох різних лабораторіях здійснювався експеримент з опріснення морської води за допомогою трьох опріснювачів. Кожний експеримент для кожного опріснювача в кожній лабораторії проводився тричі. Наслідки опріснювання, виражені у відсотках, наведені в таблиці:
|
Ступінь впливу В |
Ступінь впливу А |
||
|
А1 |
А2 |
А3 |
|
|
В1 |
3,6; 3,9; 4,1 |
2,9; 3,1; 3,0 |
2,7; 2,5; 2,9 |
|
В2 |
4,2; 4,0; 4,1 |
3,3; 2,9; 3,2 |
3,7; 3,5; 3,6 |
|
В3 |
3,8; 3,5; 3,6 |
3,6; 3,7; 3,5 |
3,2; 3,0; 3,4 |
|
В4 |
3,4; 3,2; 3,2 |
3,4; 3,6; 3,5 |
3,6; 3,8; 3,7 |
При рівні значущості a = 0,05 перевірити, чи існує вплив факторів А і В, а також спільної дії А і В на кінцевий результат експерименту.
Розв’язання. Використовуючи формули з табл. 3 лекції №9, дістанемо табл.:
|
Ступінь впливу |
Ступінь впливу фактора А |
Середня |
Загальна |
||||||||
|
А1 |
А2 |
А3 |
|||||||||
|
перший рівень |
блочна середня |
другий рівень |
блочна середня |
третій рівень |
блочна середня |
||||||
|
В1 |
Перший рівень |
3,6; 3,8; 4,1 |
|
2,9; 3,1; 3,0 |
|
2,7; 2,5; 2,9 |
|
|
|||
|
В2 |
Другий рівень |
4,2; 4,0; 4,1 |
|
3,3; 2,9; 3,2 |
|
3,7; 3,5; 3,6 |
|
|
|
||
|
В3 |
Третій рівень |
3,8; 3,5; 3,6 |
|
3,6; 3,7; 3,5 |
|
3,2; 3,0; 3,4 |
|
|
|||
|
В4 |
Четвертий рівень |
3,4; 3,2; 3,2 |
|
3,4; 3,6; 3,5 |
|
3,6; 3,8; 3,7 |
|
|
|||
|
Середня величина |
|
|
|
||||||||
|
|
Сума квадратів відхилень |
Число ступенів свободи |
Статистичні оцінки
дисперсії |
||||||||
|
Фактор А |
|
p – 1 = 2 |
|
||||||||
|
Фактор B |
|
q – 1 = 3 |
|
||||||||
|
Одночасний вплив |
|
(p – 1)´ |
|
||||||||
|
Вплив випадкових |
|
N – pq = 24 |
|
||||||||
|
Загальна дисперсія |
|
N – 1 = 35 |
|
||||||||
![]()
Визначимо спостережувані значення статистичних критеріїв за кожним фактором А, В та їх сумісної дії:
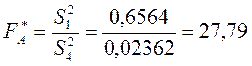 ;
;
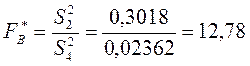 ;
;
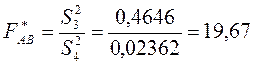 ;
;
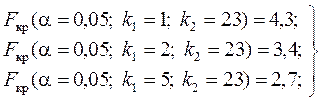 за таблицею
(додаток 7).
за таблицею
(додаток 7).
Висновок. Оскільки ![]() , то нульова гіпотеза про
відсутність впливу фактора А відхиляється, аналогічно
, то нульова гіпотеза про
відсутність впливу фактора А відхиляється, аналогічно ![]() ,
, ![]() ,
а це інформує про те, що нульова гіпотеза про відсутність впливу фактора В,
а також сумісної дії факторів А і В також відхиляється.
,
а це інформує про те, що нульова гіпотеза про відсутність впливу фактора В,
а також сумісної дії факторів А і В також відхиляється.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.