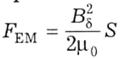
діє на феромагнітні осердя, в проміжку між торцями яких є магнітне поле (рис. 8.19), де В5 – магнітна індукція в проміжку; S - площа поверхні, зверненої до проміжку (сили ГЕМ спрямовані так, що стягують осердя).
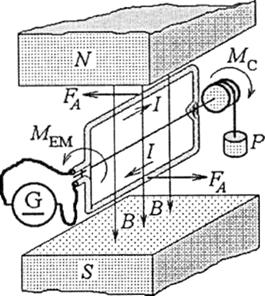
Рис. 8.18
в) механічні сили діють у магнітному полі на постійні магніти, як, наприклад, намагнічена стрілка (рис. 8.20): вона розташовується уздовж силових ліній (за напрямком векторів індукції В магнітного поля, що створюється іншим постійним магнітом), причому різнойменні полюси магнітів притягуються, однойменні - відштовхуються.
На закінчення зауважимо, що принцип дії електротехнічних пристроїв майже завжди оснований на використанні індукуючої або силової дії магнітного поля або обох водночас.
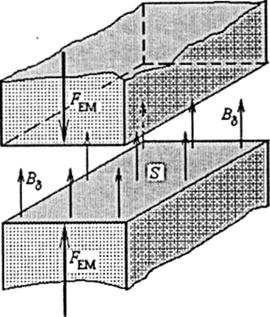
Рис. 8.18
11. Закони магнітних кіл
Досить точний розрахунок магнітних полів, зображених на рис. 8.11-8.14 і у разі більш складних електромагнітних систем, потребує застосування спеціальних польових методів розрахунку.
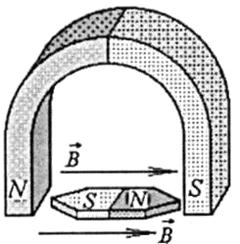
Рис. 8.20
Вони засновані на розв'язанні першого рівняння із системи рівнянь електромагнітного поля, сформульованої Максвеллом, а саме, рівняння:
![]()
де Н, J - вектори напруженості магнітного поля і густини струму.
Для магнітних кіл, в яких просторова структура магнітного поля досить очевидна, використовуються простіші методи розрахунку, засновані на законах Ома і Кірхгофа. Такі закони для магнітних кіл ці вчені не формулювали. А назви законів запозичені з електричних кіл у зв'язку з формально близькою аналогією між названими законами для цих і магнітних кіл.
Закон Ома для магнітного кола.
Розглянемо однорідну ділянку якого-небудь магнітного кола (рис. 8.21). Це може бути частина феромагнітного осердя або навіть повітряний проміжок. Ознаки однорідної ділянки такі ж, як і однорідного магнітного кола.
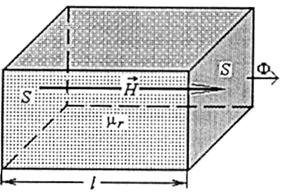
Рис. 8.21
А саме, щоб у магнітному колі виділити однорідну ділянку, на всій її довжині І напруженість магнітного поля Н повинна бути постійною. З урахуванням відомих співвідношень (8.1) і (8.3) маємо:
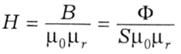
Звідси випливає, що для забезпечення Н = const однорідна ділянка магнітного кола повинна мати такі зовнішні ознаки:
1) відсутність в її межах відгалужень магнітного потоку (Ф = const);
2) постійність площі поперечного перерізу (S = const);
3) однорідність матеріалу з магнітних властивостей (μr = const).
Розглянемо спад магнітної напруги (8.7), (8.9) на довжині однорідної ділянки з урахуванням (8.15):
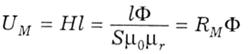
Тут окрема частина RM називається магнітним опором:
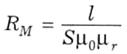
З урахуванням цього формулюється закон Ома для однорідної ділянки магнітного кола: спад магнітної напруги дорівнює добутку магнітного опору і магнітного потоку:
UM=RMФ
Це формально схоже з законом Ома U = RI для електричного кола, де також фігурують напруга U і опір R, але електричні, а магнітний потік формально можна уподібнити електричному струму І.
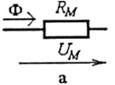
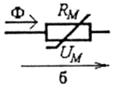
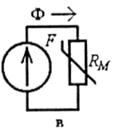
Рис. 8.22
Тепер однорідну ділянку магнітного кола (рис. 8.21) можна замістити лінійним магнітним опором (рис. 8.22, а), що відповідає неферомагнітним ділянкам, де μг ≈ 1, або нелінійним магнітним опором (рис. 8.22, б), що відповідає феромагнітним ділянкам, де μг = var (змінна величина, бо залежить від В і Н).
Для однорідного магнітного кола (рис. 8.7) магні-топровід, природно, являє собою єдину однорідну ділянку. Тому, з урахуванням (8.7), можна замість (8.18) записати модифікацію закону Ома:
F=RMФ
і використати схему заміщення такого кола у відповідності з рис. 8.22, в, де F - MPC котушки за (8.4).
Перший закон Кірхгофа для магнітного кола: алгебраїчна сума магнітних потоків, які сходяться в його розгалуженні, дорівнює нулю:
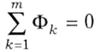
де m - кількість віток у розгалуженні магнітопроводу.
Так, на рис. 8.23, а зображено розгалуження магнітного кола, наприклад, як фрагмент рис. 8.15, б, а на рис. 8.23, б - його схематичне подання. З урахуванням позначень напрямків магнітних потоків:
Ф1-Ф2+Ф3=0
Цей закон Кірхгофа заснований на безперервності силових ліній, так що сумарний магнітний потік для замкненої поверхні завжди дорівнює нулю.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.