Взаимодействие рентгеновского излучения с веществом, страница 3

между векторами и называется углом рассеяния. Введем прямоугольную систему координат таким образом, чтобы вектора и лежали в плоскости xz. Так как вектор напряженности электрического поля  первичного излучения перпендикулярен , то очевидно, что  лежит в плоскости yz.

Под влиянием напряженности электрон получает ускорение

В соответствии с законам классической электродинамики, амплитуда напряженности Е_е электрического поля, создаваемого колеблющимсяся зарядом на расстояния R, определится уравнением

                                          (2.2)

где φ – угол между направлением движения колеблющегося заряда и направлением , с – скорость света. Анализ проведем в гауссовской системе единиц CГC традиционной при решении задач рассеяния излучения.

Подставляя в (2.2) значение ускорения, получим

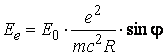                                  (2.3)

Формула (2.3) устанавливает связь между амплитудами Е_е и  электрического поля рассеянного и первичного излучений.

Так как интенсивность рентгеновского излучения (как и любого другого излучения электромагнитной природы), согласно закону Умова-Пойнтинга, пропорциональна квадрату амплитуды напряженности электрического поля, то отношение интенсивности I_e рассеянного излучения в точке А(R, 2υ) к интенсивности I₀ первичного излучения в точке 0 равно

,

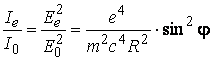откуда 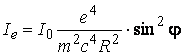                                                      (2.4)

Учитывая, что первичный луч не поляризован, то вектор занимаетлюбое равновероятное положение в плоскости yz. Всякое неполяризованное излучение (вектор ) можно разложить на две перпендикулярные друг другу поляризованные компоненты ( и ) (см. рис.2.4). Отсюда, . Усредняя по всем возможным направлениям , ввиду равновероятности этих направлений, получим для среднеквадратичного значения составляющей

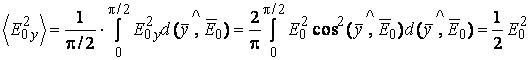
Аналогично, для среднеквадратичного значения  найдем . Тогда , и следовательно, интенсивность первичного излучения в точке 0 равна. Интенсивность I_e рассеянного излучения в точке А(R, 2υ) можно представить суммой интенсивностей I_ey и I_ez, обусловленных соответственно компонентами I_0y и I_0z первичного луча: . Согласно (2.4) получим