23
3.ОПРЕДЕЛЕНИЕ КООРДИНАТ СУДНА И ПОПРАВКИ
ШКАЛЫ ВРЕМЕНИ ПОТРЕБИТЕЛЯ .
3.1. Линеаризация результатов первичных измерений в ССЗ.
3.1.1. Зададимся горизонтной системой координат, начало которой совпадает с ближайшей к судну счислимой точкой. Полагаем, что при этом –как отмечалось в п.2.3.1 - действует программа перевода банка измеренных данных об ИСЗ из инерциальной геоцентрической системы в выбранную, где итоги первичной обработки сигналов - формулы (1,9) вида rрkизм.ог=rрk-d, где rрk=[(xk-X)2+(yk–Y)2+(zk–Z)2]1/2 и d=сгрDtап - позволяют (для определения 3-х координат X,Y,Z приемной антенны и величины d, пропорциональной искомой поправке к шкале времени потребителя) записать систему не менее 4-х нелинейных уравнений
rрkизм.ог=[(xk-X)2+(yk–Y)2+(zk–Z)2]1/2-d, k=1,2…n. (3.1)
В современной аппаратуре эта система линеаризуется поскольку каждое истинное расстояние rрk от АП до ИСЗ незначительно отличаются от расстояния Rk=(xk2+yk2+zk2)0,5 между счислимой точкой и ИСЗ из-за чрезвычайной малости X, Y, Z. Поэтому в разложении rрk по формуле Маклорена можно оставить лишь линейные члены и полагать
rпk=Rk+(drпk/dX)X +(drпk/dY)Y +(drпk/dZ)Z (3.2)
причем частные производные находятся в счислимой точке, где X=0,Y=0,Z=0. После соответствующих выкладок выражение коэффициента перед Х получается в виде
drпk/dX={-( xk-X) [(xk-X)2+(yk–Y)2+(zk–Z)2]-1/2}X=Y=Z=0=-xk(xk2+yk2+zk2)--0,5
что с обратным знаком в точности равно направляющему косинусу схk угла между радиусом-вектором Rk=Rk(x0cxk+y0cyk+z0czk)Rk=Rk(x0cxk+y0cyk+z0czk),и осью абсцисс. Аналогично выражаются и коэффициенты перед Y и Z. Поэтому (3.2) заменяется равенством rgk=Rk-Xcxk - Ycyk-Zczk. Обозначая разность между счислимым и измеренным расстояниями до ИСЗ через rk=Rk-rпkизм, получим вместо (3.1) линейную систему уравнений
Xcxk+Ycyk+Zczk+d =rk , k=1,2,…n, (3.3)
которая является совместной лишь при n=4.
3.2. Обработка квазидальностей до 4-х ИСЗ.
В этом случае совместную систему (3.3) при k=1,2,3,4 удобно записать в обычном и матричном виде:
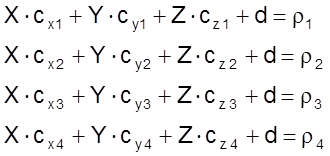 или
или 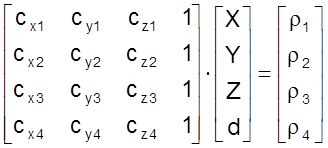 . (3.4)
. (3.4)
24
Решение этих уравнений через главный ![]() и частные
и частные ![]() ,
,
![]() ,
, ![]() определители
представим в виде линейной комбинации результатов измерений на коэффициенты
определители
представим в виде линейной комбинации результатов измерений на коэффициенты ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
равные отношению соответствующих алгебраических дополнений к
,
равные отношению соответствующих алгебраических дополнений к ![]() :
:
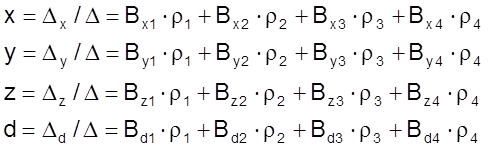 (3.5)
(3.5)
где, например,
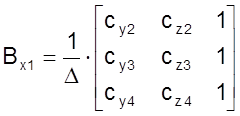 ;
; 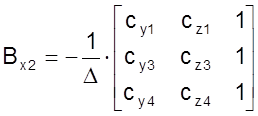 ; ... и т. д..
; ... и т. д..
Оценка погрешностей определения искомых параметров X,Y,Z,d упрощается
в предположении одинаковости дисперсий sr=sr=srk (из-за
одинаковости условий приема сигналов различных ИСЗ) и некоррелированности
результатов (1.9) первичных измерений, когда применимо известное из теории
вероятностей правило (см. с.326-327 [1]): дисперсия линейной комбинации
случайных величин равна произведению дисперсии ![]() на
сумму квадратов коэффициентов. Корень из этой суммы – как зависящей в нашей
задаче лишь от взаимного геометрического расположения ИСЗ и судна – называют
геометрическим фактором, обозначая Г с нижним индексом искомого параметра.
Применительно к решениям (3.5) системы (3.6) указанные обстоятельства
позволяют записать совокупность используемых и далее равенств:
на
сумму квадратов коэффициентов. Корень из этой суммы – как зависящей в нашей
задаче лишь от взаимного геометрического расположения ИСЗ и судна – называют
геометрическим фактором, обозначая Г с нижним индексом искомого параметра.
Применительно к решениям (3.5) системы (3.6) указанные обстоятельства
позволяют записать совокупность используемых и далее равенств:
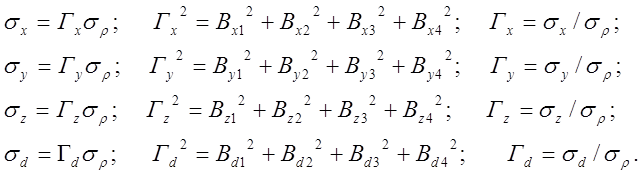 (3.6)
(3.6)
Используют
и понятия геометрического фактора погрешностей местоопределения на поверхности
Земли ![]() и в пространстве
и в пространстве ![]() , причем:
, причем:
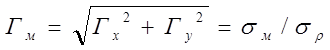
![]() ,.
(3.7)
,.
(3.7)
3.3. МНК - обработка квазидальностей до n> 4-х ИСЗ
В этом случае используется метод наименьших квадратов (МНК). Несовместнаую систему (3.3) перепишем в матричном виде
25
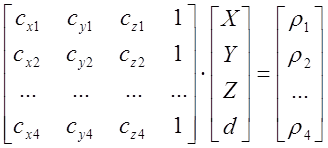 или QП=Р, (3.8)
или QП=Р, (3.8)
где П – матрица-столбец из четырех искомых параметров, Р – матрица-столбец из n измеренных величин rI , I=1,2,..n, Q – матрица (известных параметров) из четырех столбцов и n строк. В МНК уравнение (3.3) заменяется системой уравнений начальных погрешностей – разностей ek между аналитическими функциями (выражающими ожидаемые результаты измерений через искомые параметры) и реальными результатами измерений
Xcxk+Ycyk+Zczk+d-rk=ek , k=1,2,…n или QП-Р=e, (3.9)
где e,- матрица столбец из n элементов eI .
По МНК искомые параметры X,Y,Z,d находятся (подбираются или –как в нашем случае - аналитически выражаются) так, чтобы минимизировалась сумма L квадратов погрешностей
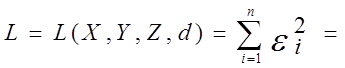 eТ.e = (P-QП)T(P-QП), (3.10)
eТ.e = (P-QП)T(P-QП), (3.10)
где, как обычно, верхний индекс «т» обозначает операцию транспонирования матрицы. Приравняв нулю частные производную от L по искомым четырем параметрам получим систему четырех линейных уравнений. Решение этой системы после громоздких аналитических выкладок (легко реализуемых в ЭВМ) выражается в компактном виде
П=(QтQ)-1QтР, (3.11)
где верхний индекс «-1» обозначает операцию определения обратной матрицы.
3.4. Возможности определений по n<4 ИСЗ
Необходимость в таких определениях может возникнуть при плавании в фиордах, прохождении под мостами и других подобных ситуациях, когда количество «видимых» ИСЗ может существенно уменьшиться.
При радиовидимости трех ИСЗ целесообразно использовать апрлрную инфориацию о высоте Z расположения приемной антенны над поверхностью эквивалентного Земле референц эллипсоида, решая систему (3.4) с соответственно меньшим числом строк и априорным Z. Необходимо учитывать влияние приливов и отливов и наличие на поверхности Океана районов (например - Бермудский треугольник), расположенных на » 50 м ниже референц-эллипсоида.
Если измерены квазидальности только по 2-м ИСЗ, то определение поверхностных координат возможно при использовании значения d, полученного в процессе предшествующих расчетов.
26
3.5. Определение координат судна по фазе cигнала одного ИСЗ
Такой режим определения места судна по результатам измерения фазы несущей был единственным в низкоорбитальных СРНС (/1/гл.12) первого поколения с Н»1000 км.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.