Исследование типовых динамических звеньев систем автоматического управления

                                           КАФЕДРА ТСС

Лабораторная работа по курсу

«Автоматизация судовождения»

ИССЛЕДОВАНИЕ ТИПОВЫХ ДИНАМИЧЕСКИХ ЗВЕНЬЕВ

Цель работы: Изучение переходных процессов в типовых динамических звеньях систем автоматического управления. Исследование влияния параметров звеньев на характер переходных процессов.

Краткое описание работы:

Для описания динамических звеньев любого  типа можно использовать дифференциальное уравнение 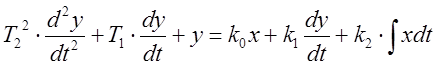(1):

                                  (1)

Из этого общего уравнения можно получить частные уравнения динамики для каждого из типовых динамических звеньев, задавая постоянные времени  и коэффициенты передачи   равными, или неравными нулю. Например, при

 получаем дифференциальное уравнение инерционного звена первого порядка, а при  получаем уравнение идеального интегрирующего звена.

Дифференциальное уравнение (1) решается простейшим методом численного интегрирования – методом Эйлера. Суть метода – на каждом малом шаге интегрирования  сначала находятся производные переменные, а затем - значения переменных, путем умножения производных на интервал интегрирования  и суммированием с предыдущим значением переменных.

В теории автоматического управления принято изучать переходные процессы при единичном ступенчатом воздействии на входе. Т.е.  при ;  при .

Соответственно, производная   теоретически должна достигнуть бесконечности  при   и равна нулю при . Однако, при реализации методов численного интегрирования в ЭВМ, значение производной ограничивается величиной . Интеграл от единичного ступенчатого воздействия равен нулю при  и линейно нарастает  при .

Порядок выполнения работы

            На экране отображаются графики переходных процессов в типовых динамических звеньях. Меняя параметры времени и коэффициентов передачи, осуществляется переход от одного типа звена к другому, или изменение переходных процессов, в зависимости от моделируемого процесса.

Параметры   изменяются линейкой прокрутки (перемещением мышью движка линейки прокрутки). Значения переменных указаны в нижней части экрана в текстовых окнах.

После установки новых значений нажимается кнопка «График» на экране  и на экране появляются графики моделируемого переходного процесса, при этом сохраняются предыдущие графики, для удобства сравнения графиков и анализа. Очищение экрана производится нажатием клавиши «CLS»,  и тогда на экране воспроизведется только один график, соответствующий заданным параметрам. Аналогичная процедура осуществляется, когда параметр  обращается в ноль.

При исследовании звеньев первого порядка на дисплее изображается только график ,  а при исследовании звеньев второго порядка изображаются графики Y и ее первой производной  .

По окончанию моделирования программа возвращается к вводу новых параметров.

1.  Безинерционное звено

Задать  .

Получить и зарисовать с экрана переходный процесс. Изменяя  от 1 до 20, наблюдать за изменениями процесса. Зарисовать с экрана 2-3 характерных процесса. Сделать соответствующие выводы.

2.  Инерционное звено 1-го порядка

Задать .

Изменяя  от 0 до 20 наблюдать за изменениями переходных процессов. Зарисовать с экрана 2-3 характерных процесса. Сделать соответствующие выводы.

3.  Дифференцирующее звено

Задать      .

Получить и зарисовать переходный процесс в идеальном дифференцирующем звене.

Увеличивая  от 0 до20 наблюдать за переходными процессами в реальном дифференцирующем звене. Зарисовать с экрана 2-3 процесса, сделать выводы.

4.  Интегрирующее звено

Задать .

Получить и зарисовать переходный процесс в идеальном интегрирующим звене.

Изменяя   от 1 до 20 наблюдать за изменениями переходных процессов. Зарисовать с экрана 2-3 процесса, сделать выводы.

Задать . Увеличивая  от 0 до 20 наблюдать за переходными процессами   в реальном интегрирующем звене. Зарисовать с экрана 2-3 процесса, сделать выводы.

5.  Инерционное звено 2-го порядка и колебательное звено

Задать .  

Получить переходный процесс в инерционном звене 1 порядка.

Увеличивая от 0 до 20, а затем уменьшая  от 10 до 2, наблюдать за изменением переходных процессов. Обратить внимание на моменты перехода от звена 1-го порядка к звену 2-го порядка, а затем к колебательному звену.

Зарисовать несколько характерных процессов, сделать соответствующие выводы.

                              Отчет по работе

Отчет по лабораторной работе должен содержать:

титульный лист;

- краткую характеристику исследуемых звеньев с приложением графиков полученных переходных процессов;

-  выводы по результатам экспериментов.

Графики необходимо оформить так, чтобы они наилучшим образом отражали полученные результаты и соответствовали сделанным выводам.

              Для получения зачета необходимо повторить по учебнику или конспекту лекций теоретический материал, иметь полное представление о каждом проделанном эксперименте и его результатах, уметь ответить на контрольные вопросы, подобные приведенным ниже.

                 Контрольные вопросы

1.  Что такое «типовое динамическое звено»?

2.  Перечислить известные вам типовые динамические звенья.

3.  Что такое передаточная функция?

4.  Что такое переходная характеристика?

5.  Для каждого из типовых динамических звеньев приведите уравнение динамики, передаточную функцию и переходную характеристику.

6.  Пояснить каждый проделанный вами эксперимент и его результаты.

7.  Чем отличается реальное интегрирующее звено от идеального?

8.  Чем отличается реальное дифференцирующее звено от идеального?

9.  Чем отличается инерционное звено 2 порядка от инерционного звена 1-го порядка.

10.  Чем отличается инерционное звено 2-го порядка от колебательного.