Исследование работы САУКС в режимах маневрирования и стабилизации курса

                                               Кафедра ТСС

                                    Лабораторная работа  по курсу

                              «Автоматизация судовождения»

                                 Исследование САУКС

Цель работы:

1.  Изучить работу САУКС в режиме маневрирования, ознакомиться с оценками качества переходных процессов, произвести выбор оптимальных настроечных параметров САУКС.

2. Изучить   работу САУКС в режиме стабилизации курса при воздействии возмущений, исследовать влияние основных параметров  САУКС на качество управления.

Краткие теоретические сведения

Одним из методов исследования систем автоматического управления (САУ) является моделирование их работы на ЭВМ. На первом этапе моделирования необходимо построить математическую модель исследуемой САУ, т.е. получить систему уравнений, описывающих ее поведение. Для построения математической модели САУ используется ее структурная схема, каждый элемент которой описывается известным уравнением динамики.

          Структурная схема системы автоматического управления курсом судна (САУКС) с использованием типового авторулевого приведена на рис.1.

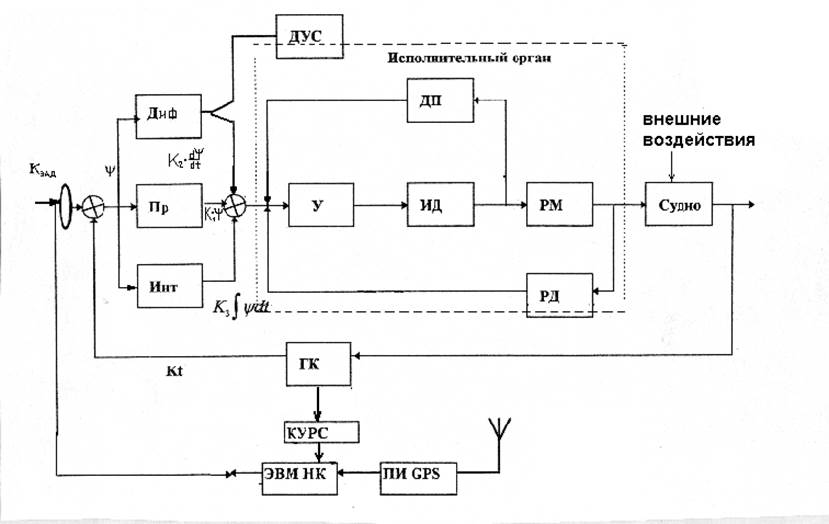
Основными элементами системы являются:

·  объект управления судно;

·  датчик регулируемого параметра (гирокомпас);

·  регулятор (основной прибор авторулевого);

·  исполнительные органы (исполнительный механизм авторулевого и рулевая машина).

Судно, как объект управления курсом, можно упрощенно представить инерционным звеном 1 порядка, имеющим уравнение динамики:

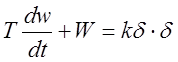                                      ,                                      (1)

   где w - угловая скорость;

  d - угол перекладки руля;

 T -постоянная времени, характеризующая инерционность судна;

 k_d - коэффициент  управляемости, равный отношению угловой скорости на установившейся циркуляции к соответствующему углу перекладки руля.

Для связи угловой скорости с мгновенным (текущим) значением курса используется простейшее уравнение:

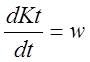.                                                      (2)

При исследовании САУКС можно считать гирокомпас безинерционным звеном с коэффициентом передачи, равным 1, поскольку его инерционность на порядок меньше, чем у других элементов системы.

          В типовых авторулевых применяются пропорционально-интегрально-дифференциальные регуляторы, выходной сигнал которых описывается следующим выражением:

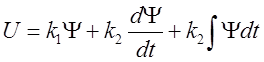                                 ,                                            (3)

где     - угол рыскания;

 – заданное значение курса;

 – фактическое значение курса;

 – коэффициенты закона управления.

Уравнение динамики регулятора преобразуем к виду, более удобному для реализации в ЭВМ, с учетом следующих замечаний:

а) так как исполнительные органы обеспечивают преобразование сигнала регулятора в пропорциональный угол кладки руля, то можно считать  заданным углом кладки руля .

б) сигнал производной угла рыскания заменим угловой скоростью:

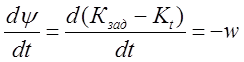                             .                                (4)

Поскольку  заданный курс есть величина постоянная, за исключением малого времени поворота задающего штурвала.

в) взамен интеграла от угла рыскания введем новую переменную .

С учетом этих трех замечаний уравнение регулятора (3) заменим на два уравнения:

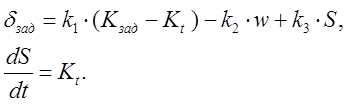                                                              (5)

На современных морских судах, в основном, применяют электрогидравлические рулевые машины, у которых скорость перекладки пера руля пропорциональна величине смещения управляющего органа от нейтрального положения. То есть, можно представить рулевую машину идеальным интегрирующим звеном с единичным коэффициентом передачи. Тогда уравнение динамики исполнительных органов (исполнительный механизм авторулевого плюс рулевая машина) будет иметь вид:

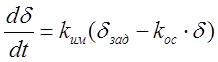                                ,                                               (6)

где   – коэффициент передачи исполнительного механизма;

 – коэффициент обратной связи (коэффициент передачи рулевого датчика), равный 0.2 – 2.0.

Коэффициент передачи исполнительного механизма (результирующий коэффициент передачи усилителя и двигателя,  охваченных обратной связью через датчик скорости перекладки ДСП) определяется по формуле:

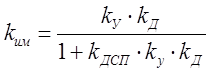                                         ,                                       (7)

где  – коэффициенты передачи усилителя, двигателя и датчика скорости перекладки соответственно.

Численное значение  обычно равно 0.3 – 0.5. Это означает, что сигнал на выходе регулятора, соответствующий 3 градусам заданной перекладки руля, вызовет перекладку руля со скоростью 0.09 - 1.5 град/сек.

          Таким образом, для моделирования работы САУКС на ЭВМ используется следующая система дифференциальных уравнений:

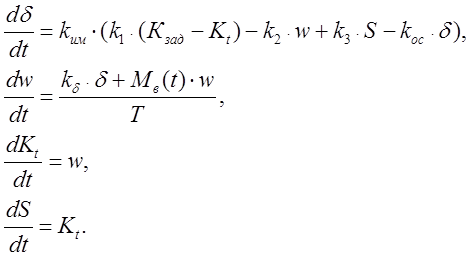                                    (8)

Для решения данной системы уравнений используется метод численного интегрирования – метод Эйлера. Согласно этого метода, в правые части уравнений подставляют значения переменных в начальный момент времени и находят значения производных в начальный момент времени. Затем для заданного шага интегрирования (малого интервала времени ) находят приращения переменных за шаг интегрирования, умножая значение производных в начальный момент времени на . Далее находят значения переменных в начале второго шага интегрирования, суммируя полученные приращения с начальными значениями переменных. На втором шаге интегрирования в правые части уравнений системы подставляют значения переменных в начале второго шага и находят значения производных в начале второго шага. Затем рассчитывают приращения переменных за второй шаг, умножая найденные значения производных на . Далее получают значения переменных в начале третьего шага интегрирования суммируя приращения со значениями переменных в начале второго шага и т.д. до конца процесса.

При исследовании САУКС в режиме маневрирования считают отсутствующими возмущающие моменты   и полагают отключенным интегрирующее звено в регуляторе . Изменяя коэффициент обратной связи   и коэффициент при производной  (коэффициент тахогенератора ), получают различные переходные процессы при выводе судна на заданный курс - .

Качество переходных процессов в режиме маневрирования оценивается с помощью следующих показателей:

-  перерегулирование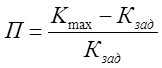 

-  время регулирования  – время, в течении которого величина динамической ошибки входит в зону заданной статической ошибки ( в настоящей работе статическая ошибка принята равной 1% от  или 0.3 град);

-  интегральная оценка качества переходного процесса:

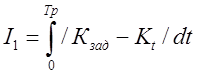                                      ,                                    (9)

минимум которой соответствует наилучшему переходному процессу и оптимальным настроечным параметрам.

          При исследовании САУКС в режиме стабилизации на курсе задаются возмущающие моменты , имитирующие действие волна корпус судна. Изменяя коэффициент обратной связи , коэффициент при производной   (коэффициент тахогенератора -) и коэффициент при интеграле () получают различные варианты процесса стабилизации.

          Для оценки качества управления в режиме стабилизации используется интегральный квадратичный критерий, величина которого пропорциональна потерям эксплуатационной скорости судна от рыскания и от перекладки руля: