Численное дифференцирование. Нахождение значений первой и второй производных в заданной точке

Численное дифференцирование

(рекомендуется для самостоятельного выполнения)

Цель работы: для функции, заданной таблично, найти значение первой и второй производных в точке .

ПРИМЕР. Функция задана таблицей 3.1.

Таблица 3.1

x	0,8	1,0	1,2	1,4	1,6	1,8	2,0	2,2
f(x)	1,17609	1,00000	0,833333	0,714285	0,625000	0,55555	0,32222	0,22222

Для приближенного вычисления значения производных функции в точке =1.8, рассмотрим методы численного дифференцирования, полученные на основе разложения функции по формуле Тейлора.

Теоретическая часть.

А. Пусть на отрезке  на неравномерной сетке задана сеточная функция , . Предположим, что . Разложим функцию  по формуле Тейлора, причем количество точек , определяющих расчеты относительно точки , равнялось 1.

,

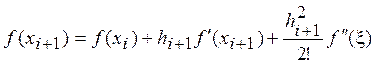где , .

Получаем:

.

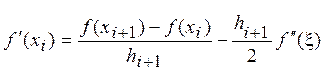Справедлива оценка:

,

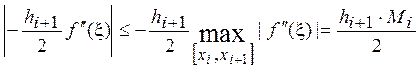где .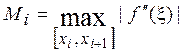

Отсюда следует функциональная формула для первой производной:

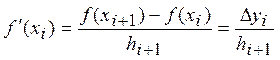,                                          (1)

причем оценка погрешности составит .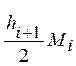

Формула (1) является левосторонней. Если функцию  разложить по формуле Тейлора относительно точки , то получим правостороннюю формулу:

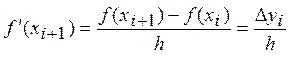,                                        (2)

оценка погрешности составит .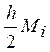

Б. Пусть на отрезке  на неравномерной сетке задана сеточная функция , . Предположим, что . Разложим функцию  при  и  по формуле Тейлора относительно точки , причем , , . В результате разложения находим соотношения:

,

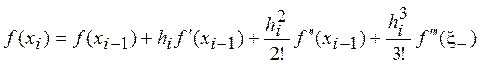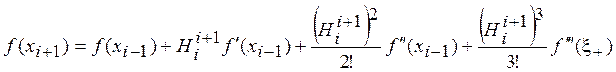где , , .

Исключаем в приведенных выше равенствах вторую производную, и выражаем из полученных соотношений , получаем следующую аппроксимацию первой производной в крайней левой точке:

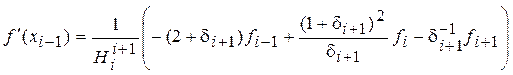,    (3)

 где 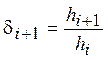, оценка погрешности , .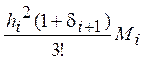

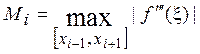На равномерной сетке (, ) формула (3) приводится к виду:

,

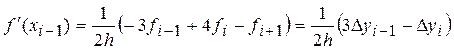оценка погрешности составляет , .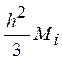

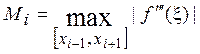Аналогично, разложив функцию  относительно точки  и получив соотношения для , , найдем , аппроксимирующую первую производную в правой крайней точке:

,

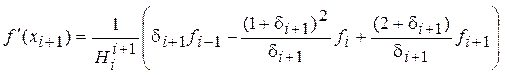с оценкой погрешности 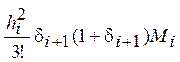.                             (4)

Для равномерной сетки (, ):

.

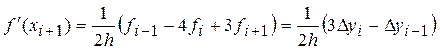С. Пусть на отрезке  на неравномерной сетке задана сеточная функция , . Предположим, что . Разложим функцию  при  и  по формуле Тейлора относительно центральной точки , причем . Полученные выражения для ,  и исключение из них слагаемых со второй производной приводят к следующим расчетным формулам, аппроксимирующим первую производную в центральной точке :

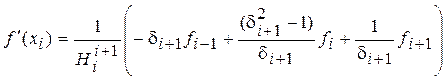.                 (5)

Для равномерной сетки (, ):

,

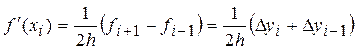оценка погрешности составляет , .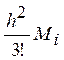

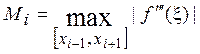D. Пусть на отрезке  на неравномерной сетке задана сеточная функция , . Предположим, что . Разложим функцию  в точках  и  по формуле Тейлора до слагаемого четвертого порядка относительно шага.

Аппроксимация второй производной  на нерегулярном шаблоне имеет вид:

.

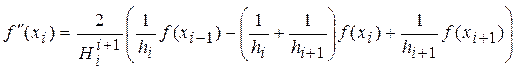Если сетка равномерная, то

,

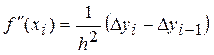оценка погрешности составляет , .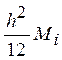

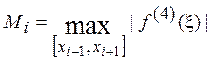Пример для расчета.

Требуется вычислить значение первой производной  и второй производной .

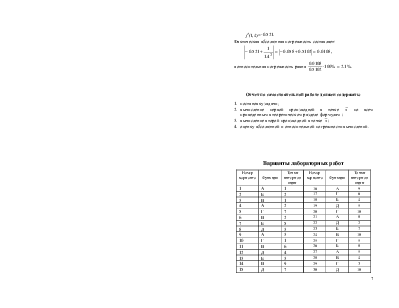
1. Так как шаг заданной сеточной функции постоянный ,  точка  находится внутри сетки, то для вычисления производной в этой точке воспользуемся формулой (5). При этом центральная точка расчетного шаблона совпадает с точкой

Посчитаем искомое значение производной:

=.

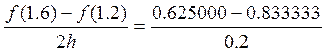Прежде чем выполнить вычисление, определим количество знаков, которое сохраняется при этом.

Остаточное слагаемое выбранной формулы

Так как остаточное слагаемое , то в вычислениях ожидается три верных цифры после запятой. Оставим ещё одну сомнительную, итого для наших расчетов четыре цифры после запятой.

=-0.521.

Фактическая абсолютная погрешность составляет:

,

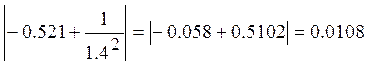а относительная погрешность равна .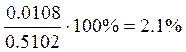

Отчет по самостоятельной работе должен содержать:

1.  постановку задачи;

2.  вычисление первой производной в точке  по всем приведенным в теоретическом разделе формулам ;

3.  вычисление второй производной в точке ;

4.  оценку абсолютной и относительной погрешности вычислений.

Варианты лабораторных работ

Номер варианта	Функция	Точки интерполяции	Номер варианта	Функция	Точки интерполяции
1	А	1	16	А	9
2	Б	2	17	Г	6
3	В	1	18	Б	4
4	А	2	19	Д	5
5	Г	7	20	Г	10
6	В	2	21	А	8
7	Б	5	22	Д	2
8	Д	3	23	Б	7
9	А	3	24	В	10
10	Г	1	25	Г	5
11	В	6	26	Б	8
12	Д	4	27	А	5
13	Б	3	28	В	4
14	В	9	29	Г	3
15	Д	7	30	Д	10

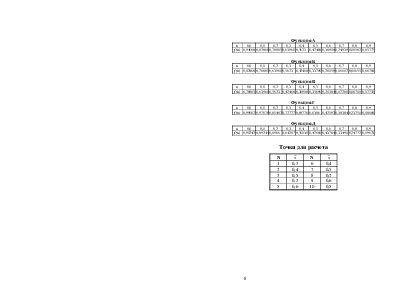
Функция А

x	0,0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
f(x)	0,94608	0,82868	0,70805	0,63961	0,5623	0,42468	0,38918	0,24959	0,10582	0,05777

Функция Б

x	0,0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
f(x)	0,82868	0,70805	0,63961	0,5623	0,42468	0,33790	0,20159	0,16117	0,01655	0,00768

Функция В

x	0,0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
f(x)	0,70805	0,63961	0,5623	0,42468	0,38918	0,35096	0,21384	0,17260	0,10711	0,57735

Функция Г

x	0,0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
f(x)	0,99602	0,97670	0,85402	0,72777	0,69776	0,6386	0,42592	0,38384	0,23751	0,18688

Функция Д

x	0,0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
f(x)	0,91242	0,89244	0,6906	0,64207	0,51130	0,47660	0,43784	0,33491	0,24772	0,19623

Точки для расчета

N		N
1	0,3	6	0,4
2	0,4	7	0,3
3	0,5	8	0,2
4	0,2	9	0,6
5	0,6	10	0,5