Задача на определение перемещений или деформаций

Основная задача

Независимо от того, велики или малы перемещения ( или деформации), внутренние и внешние силы должны удовлетворять условиям равновесия. Если перемещения определяются конечным числом (узловых) параметров , то должно выполняться равенство

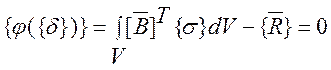, (1)

где  - сумма внешних и внутренних обобщенных сил, а матрица  определяется из соотношения

. (2)

При больших перемещениях деформации нелинейно зависят от перемещений и матрица  зависит от .

,  (3)

где ­матрица, определяющая бесконечно малые деформации, а матрица  зависит от перемещений.  в общем случае является линейной функцией перемещений.

Если деформации не очень велики, то можно использовать обычное соотношение теории упругости

, (4)

где  - обычная матрица упругих постоянных.

Обнако в равной степени можно было бы использовать и любое нелинейное соотношение между напряжениями и деформациями, поскольку задача сводиться к решению нелинейной системы уравнений (1).

 При использовании метода Ньютона необходимо найти зависимость между  и . Варьируя (1) по , получаем

2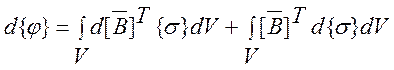. (5)

Используя формулы (4) и (2)  находим

,

а на основании (3) имеем

.

Поэтому

,

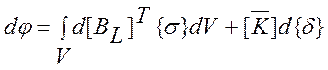где

,

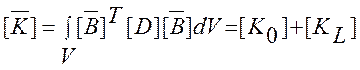а  является обычной матрицей жесткости при малых деформациях, т.е.  имеет вид

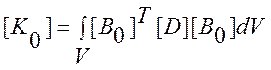.  (7)

Матрица  появляется благодаря тому, что перемещения велики. Она определяется выражением

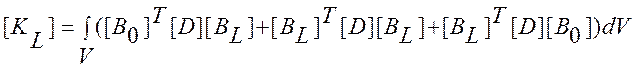. (8)

Матрица  известна как матрица начальных перемещений, матрица больших перемещений и т.п. Эту матрицу можно построить, считая деформации малыми, но учитывая изменения координат элемента при вычислении жескостей.