Численное дифференцирование и интерполяция

Численное дифференцирование и интерполяция

Цель работы:

по заданной таблице найти значения первой и второй производной в узлах сетки:

а) используя разделенные разности;

б) с помощью интерполяционных формул 1-го и 2-го порядка.

Сравнить полученные результаты и оценить погрешность.

Варианты работ

Таблица значений функции y=y(x)

x	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0	1,1	1,2	1,3
y	1	1,1	1,2	1,3	1,5	1,8	2,3	3,1	4,4	6,5	7,9	8,5	9,1	9,8

Найти значение y, y¢ и y¢¢ при заданном x в соответствии с вариантом:

Вариант	х		Вариант	х
1.	0,16		11.	1,18
2.	0,27		12.	1,29
3.	0,38		13.	1,21
4.	0,49		14.	1,13
5.	0,51		15.	0,93
6.	0,62		16.	0,82
7.	0,73		17.	0,77
8.	0,84		18.	0,66
9.	0,96		19.	0,54
10.	1,07		20.	0,14

 Рекомендации к выполнению задания

а) Для вычисления производных во внутренних узлах сетки будем использовать центральные разделенные разности:

                                                                                                       , ,

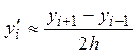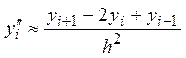где h – шаг сетки.

Эти формулы неприменимы к вычислению производных в крайних узлах. Поэтому в первом и в последнем узле сетки используем нецентральные разделенные разности:

                                                                                                          , ,

                                                                                                           , .

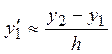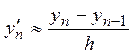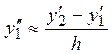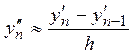б) Интерполяционные формулы первого порядка позволяют вычислить значение только первой производной между узлами сетки. Запишем «правую» и «левую» интерполяционные формулы первого порядка и найдем их первые производные для узла с номером i<n:

                                                                        ,

                                                                            ,

                                                                                                  ,

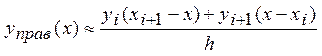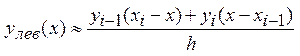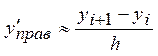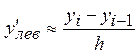
Как видно из последних формул, полученные таким образом производные совпадают с нецентральными разделенными разностями первого порядка.

Интерполяционная формула второго порядка может быть использована для отыскания и первой, и второй производной. Для ее построения используются значения функции в трех соседних узлах сетки:

         

Дифференцирование по переменной x дает формулы для вычисления производных:

          ,

          .

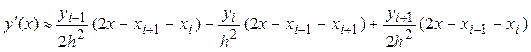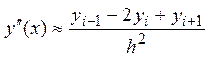Последняя формула совпадает с центральной разделенной разностью второго порядка для i-го узла. Формула для первой производной тоже совпадает с центральной разделенной разностью, если вместо переменной x подставить абсциссу i-го узла.

Для оценки погрешности интерполяции примем во внимание неточность задания исходных данных, считая, что абсолютная погрешность не превышает половины единицы последнего удержанного разряда. В нашем случае значения функции в таблице заданы с точностью до десятых, следовательно, их погрешность не превышает 0,05. Суммарная погрешность интерполяции, таким образом, складывается из погрешности вычисления по неточно заданным данным и погрешности интерполяционной формулы.

Аналогично, погрешность численного дифференцирования должна учитывать как неточность интерполяционной формулы, так и неточность задания данных.

Найденную погрешность следует проверить на правдоподобность (различие между результатами, полученными разными способами, должно укладываться в погрешность).