Исследование буровых долот с дисковыми и зубчато-дисковыми шарошками, страница 8

Рис. 2.15. Траектория движения зуба дисковой шарошки в скважине

С каждым оборотом шарошки вокруг оси скважины О- О зуб возвращается на дугу а-н (рис. 2.15), а с каждым полуоборотом – на дугу б-м. При перемещении по отрезку дуги а-ж и дуги б-ж зуб с породой не имеет контакта, т. е. разрушение породы он не производит. При перемещении по дугам ж-н и ж-м зуб с породой контактирует, осуществляя ее разрушение и образуя рабочий сектор ж-м-н. Все зубья шарошек, имея сложную траекторию движения, образуют сетку разрушения породы в скважине, величина “ячеек” которой зависит от диаметра зубчато-дисковых шарошек, количества зубьев, установленных на них, и скорости бурения (рис. 2. 16).

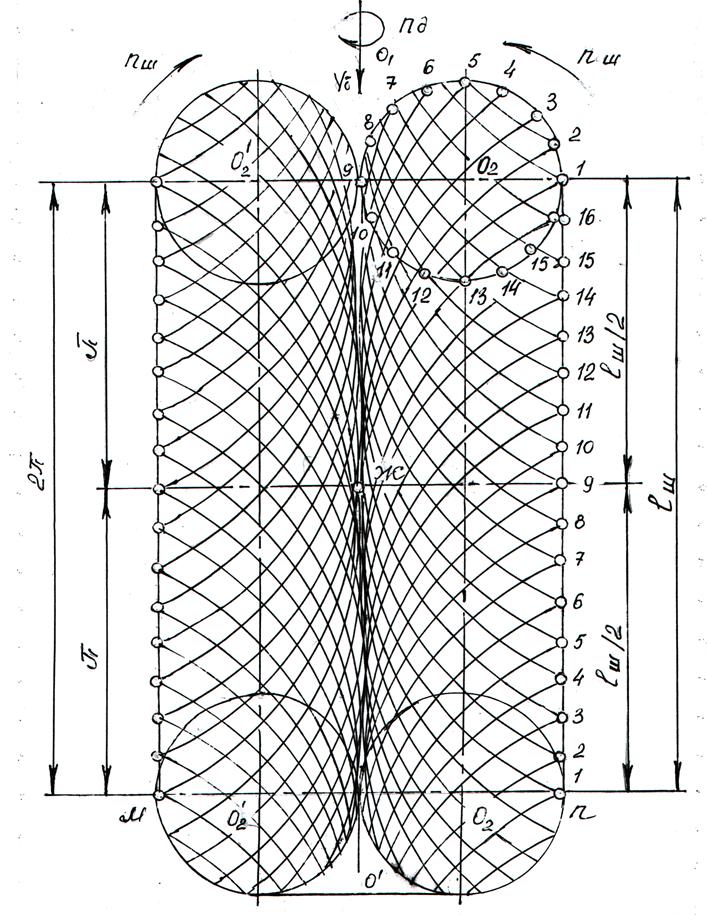
Рис. 2.16. Сетка разрушения породы в скважине зубьями шарошек

          На стойкость зубьев шарошки, а следовательно, и на стойкость долота в целом, оказывает влияние не только характер взаимодействия с породой, но и путь трения при их контакте в зоне разрушения. Для определения пути трения зуба при разрушении породы составим схему кинематической работы долота с зубчато-дисковыми шарошками (ДЗДШ-244,5) (рис. 2.17).

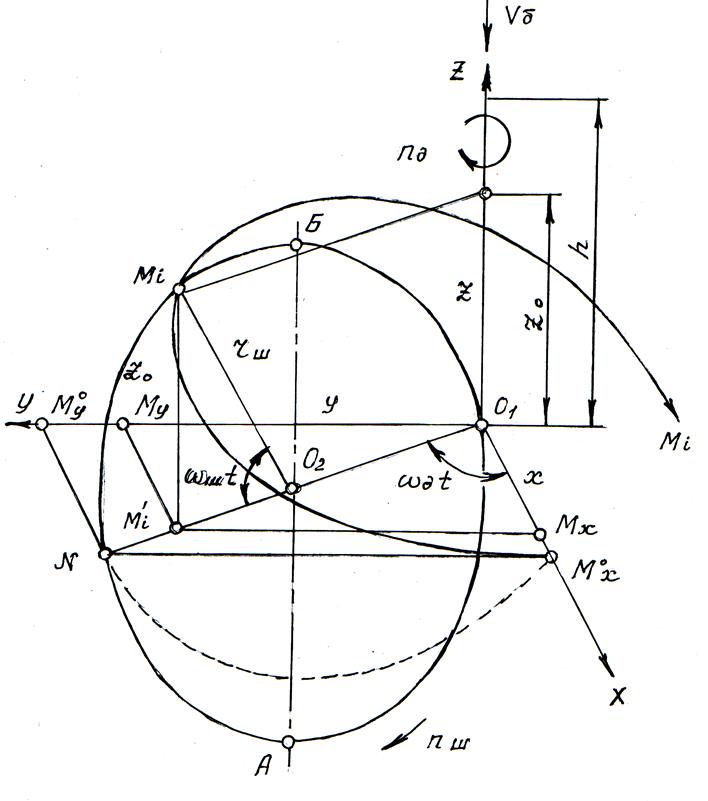
Рис. 2.17. Схема кинематической работы долота с зубчато-дисковыми шарошками

          Каждая шарошка, вращаясь вокруг вертикальной оси долота с частотой n, за один оборот проходит в скважине путь, равный внедрению долота в породу h. При этом каждый зуб шарошки опускается в скважину, перемещаясь по дуге АБ на расстояние:

                                                                               (2. 19)

а при перемещении по дуге БА на расстояние:

                                                                                (2. 20)

где - проекция т. М (зуба) на ось Z. При перемещении по образующей шарошки т. М будет иметь проекцию:

                                               ,                                (2. 21)

где - угловая скорость вращения шарошки, t –время перемещения т. М по образующей шарошки, - радиус шарошки.

Пусть т. М в начальный момент времени t находилась в т. М (рис. 2.17). При вращении вокруг вертикальной оси долота О- О с частотой вращения n т. М переместится в т. М, а при вращении с частотой n вокруг оси шарошки О - из т. N в т. М. Таким образом, за время t точка (зуб) пройдет путь по траектории из т. М в т. М. Ее проекцией на плоскости ОYХ будет т. М с координатами: х = ОМ; y = ОМ; z =ОМ.

          В общем виде координаты движения т. М, с учетом перемещения ее в указанных выше плоскостях по определенной траектории М - М - Ммогут быть представлены следующими уравнениями.

1. Из треугольника ОММ получим: Х = ОМ, где ОМ = r ОМ. Из треугольника ОММ: ОМ= r.

Таким образом, ОМ = r(1 ). Тогда

                                   .                         (2. 22)    

2. Из треугольника ОММ получим: Y = ОМ или

                                     .                        (2. 23)

3. Из треугольника ОММ получим: = r. С учетом выражений (2. 19) и (2. 20):

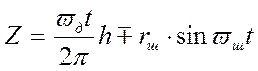                                                .                        (2. 24)

          В уравнениях (2. 22) и (2. 23) (+) следует учитывать при движении точки М от А к Б (работа зуба на периферийных участках забоя), а (-) – при движении точки М от Б к А (работа зуба на среднем участке забоя). В уравнении (2. 24) (+) следует учитывать при движении точки М от Б к А (работа зуба на среднем участке забоя), а (-) – при движении точки М от А к Б (работа зуба на периферийном участке забоя).

          Таким образом, получено параметрическое уравнение траектории точки М, то есть уравнение движения зуба, установленного на зубчато-дисковой шарошке бурового долота, при разрушении породы в скважине, которое выглядит следующим образом:

,

                                   ,                       (2. 25)

.

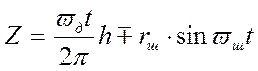В процессе бурения долото совершает двоякое движение: поступательное сверху вниз под действием осевой нагрузки от механизма подачи  и вращательное, осуществляемое  двигателем вращателя через буровые штанги. Первое движение обеспечивает внедрение долота в породу, а второе производит срезание или скалывание породы за счет крутящего момента.   

При одновременном вращении зубьев вокруг оси шарошки и относительно оси скважины изменяется радиус их вращения вокруг оси долота, практически от 0 до , однако средний радиус вращения каждого зуба за один оборот шарошки оказывается равным . Приняв допущение, что, участвуя одновременно в двух движениях, точки (зубья), находящиеся на поверхности породоразрушающих элементов, например, точки М, описывают винтовые линии со средним радиусом вращения  (рис . 2.18), определим длину пути, проходимого любой точкой, находящейся на поверхности зубчато-дисковой шарошки., в сравнении с длиной пути резцов, установленных на режущих долотах со стационарными породоразрушающими элементами.

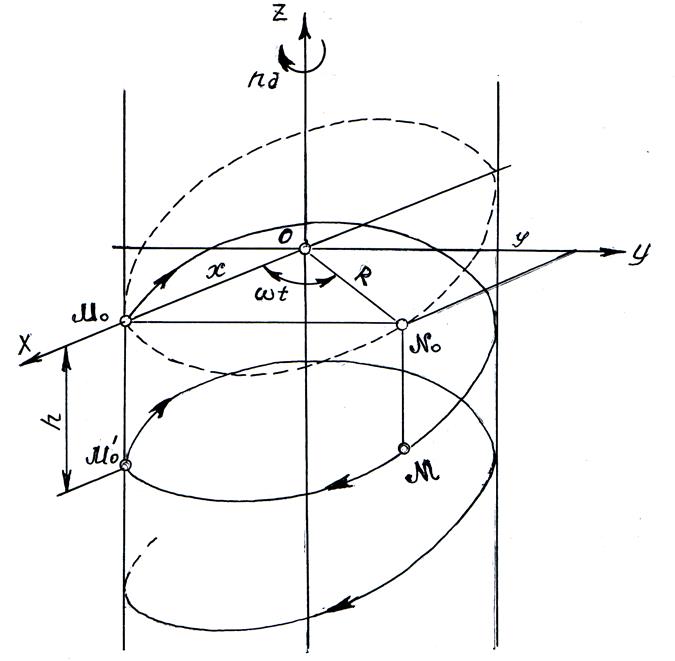
Рис. 2.18. Траектория движения зуба шарошки по среднему радиусу вращения вокруг оси долота

Координаты движения  точки М могут быть  представлены следующими уравнениями [31, 32].

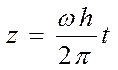;    ;    ,                (2.26)

где R – среднее расстояние (средний радиус)  точки М от  оси вращения; h – внедрение долота в забой скважины за один оборот.

Проекция N точки М на плоскость ОХY имеет координаты: х = R cost; у = R sint и Z = 0. Поскольку для точки N угол поворота α(t) = t, то она совершает один оборот вокруг точки О, находящейся на оси вращения долота, по окружности радиусом R за время T = 2π/, так как α(Т)=T=2π. В начальный момент времени t = 0 точки М и N находились в положении Мо (рис. 2.18).

             Аппликата Z точки М  пропорциональна времени t  и в момент времени t = Т:

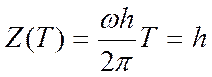                  .                                         (2. 27)

Таким образом, точка М за время Т перемещается по вертикали на расстояние h, хотя представляет  собой внедрение долота в породу за один оборот и одновременно является шагом винта.

Теперь важно отметить длину пути (витка) L, проходимого любой точкой, находящейся на поверхности лезвия или заторможенной (не вращающейся) зубчато-дисковой шарошки за один оборот долота.