Построение базисных функций: Учебное пособие

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

РЯЗАНСКАЯ ГОСУДАРСТВЕННАЯ  РАДИОТЕХНИЧЕСКАЯ АКАДЕМИЯ

И.В. ФИЛИППОВ

Е.В. ЧЕРНОВА

ПОСТРОЕНИЕ БАЗИСНЫХ ФУНКЦИЙ

Учебное  пособие

Рязань 2005

УДК  517.9

            Построение базисных функций: Учеб. пособие /И.В. Филиппов, Е.В. Чернова; Рязан. гос. радиотехн. акад. Рязань, 2005. 24 с.

          Рассматриваются методы конечно-элементной аппроксимации интегральных соотношений из уравнения типа уравнения Лапласа, способы построения одномерных, двумерных и трехмерных базисных функций разного порядка.

          Предназначено для студентов специальности 210101, изучающих курсы «Математическое моделирование электронных устройств», «ЭВМ в технике и научных исследованиях».

Ил. 16. Библиогр.: 7 назв.

Численные методы, метод конечных элементов, базисные функции

          Печатается по решению редакционно-издательского совета Рязанской государственной радиотехнической академии.

          Рецензент:  кафедра общей и экспериментальной физики РГРТА

                              (зав. кафедрой проф. Э.П. Шеретов)

Построение базисных функций

Одномерное поле

Рассмотрим задачу нахождения математического выражения функции u(x), описывающей в одномерном случае распределение потенциала вдоль оси  x, как показано на рис. 1,а.

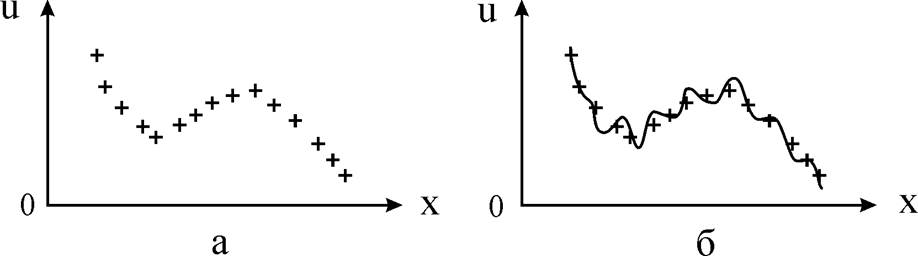
Рис.1. Распределение потенциала вдоль оси X

В приближении можно использовать полином:

 ,                                                                    (1)

в котором коэффициенты a, b, c, и d определяются по методу наименьших квадратов. По мере увеличения  степени полинома выражение (1) будет более точно соответствовать истинному значению потенциала. Однако при этом может возникнуть проблема: при малой степени полинома выражение (1) достаточно точно соответствует данным, но при увеличении степени могут возникнуть осцилляции в распределении потенциала, как показано на рис. 1,б.

Чтобы устранить этот недостаток, оставляя при этом малую степень полинома, участок 1-2, в соответствии с методом конечных элементов, разбиваем на подобласти, называемые элементами, которые описываются полиномами малой степени.

Введем параметр S, характеризующий расстояние вдоль оси x. На рис. 2,a потенциал представляется в виде функции этого расстояния.

На рис. 2,б рассматриваемая функция разбита для примера на три подобласти (элемента), в пределах которых она аппроксимируется линейными полиномами вида (1).

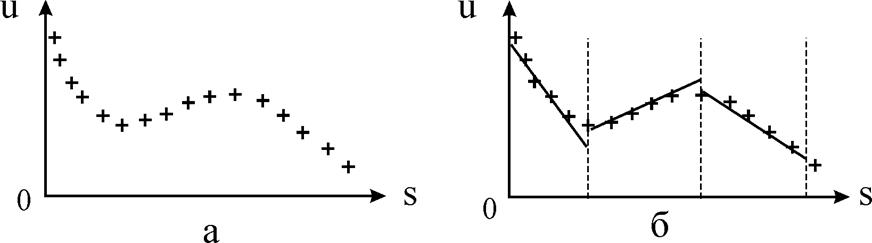
Рис. 2. Потенциал как функция нормированного расстояния S

Линейные  базисные функции

Из рис. 2,б можно видеть, как возникает новая проблема: на распределении потенциала u вдоль s появляются разрывы на границах элементов. Для того чтобы состыковать значения функции на границах, или «сшить» их поступим следующим образом. Заменим в первом элементе константы a и b параметрами u₁ и u₂, которые определяются значением потенциала u на концах элемента, и определим линейную зависимость между этими двумя значениями как

,                                                                                                      (2)

где x  - нормированное расстояние вдоль оси (0 £ x £ 1).

Введем величины

     и                                                                                                            (3)

таким образом, что

.                                                                        (4)

Функции, задаваемые выражением (3), называются базисными функциями, ассоциированными с узловыми параметрами u₁ и u₂.

Базисные функции j₁(x) и j₂(x) – линейные функции, которые на графике будут иметь вид прямых линий (рис. 3), значения которых  изменяются в пределах от 0 до 1.

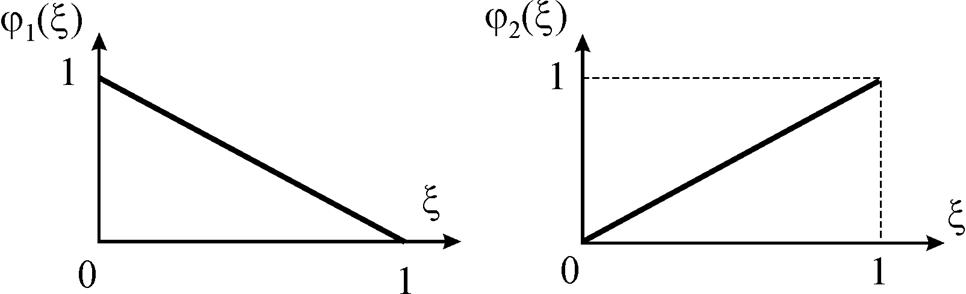
Рис. 3. Линейные базисные функции

Обычно потенциал в узлах u_nассоциируют с узлом элемента n и вводят потенциал U_D, определяемый в глобальном узле относительно локального узла n элемента e. Для этого используют матрицу связи D(n,e):

,                                                    (5)

где D(n,e) определяется как номер глобального узла, соответствующего локальному узлу n элемента e, как показано на рис. 4.

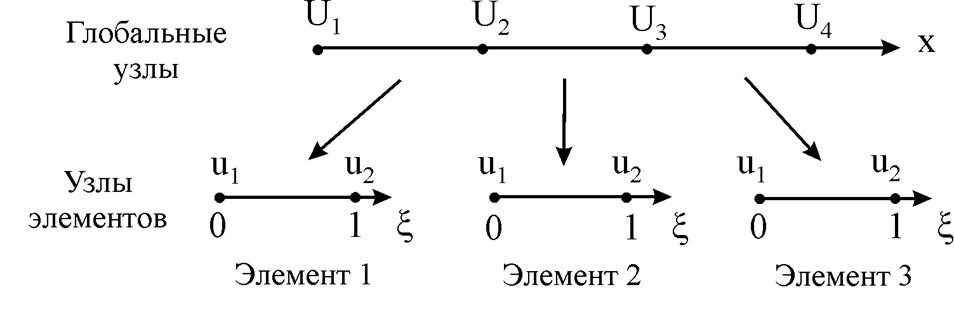
Рис. 4. Взаимосвязь между глобальными узлами и узлами элементов

Так, для первого элемента  u₁ = U₁, u₂ = U₂ и

.                                                                        (6)

На втором элементе u₁ = U₂, u₂ = U₃  и имеет место следующая интерполяция:

,                                                                        (7)

а поскольку U₂ относится как к первому, так и ко второму элементам, то распределение потенциала u(x) перестает быть дискретным и становится в этом месте непрерывным.

Аналогично потенциал на третьем элементе интерполируется выражением:

,                                                              (8)

где u₁ = U₃ и u₂ = U₄ (теперь U₃ относится и ко второму и третьему элементам).

На рис. 5. показано распределение потенциала, определенного интерполяциями (6)–(8). Видим, что теперь значения потенциала на границах элементов «сшиты».

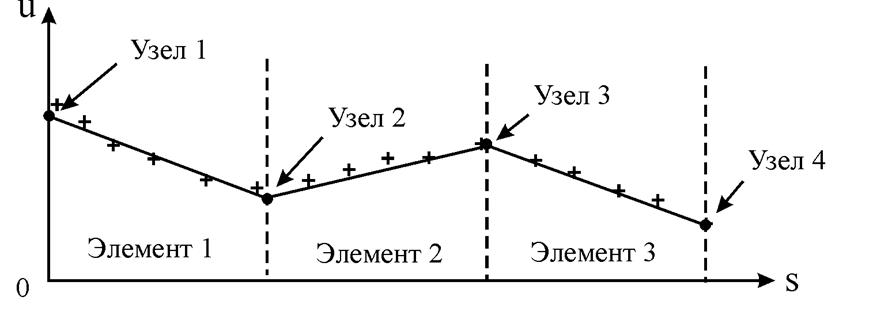
Рис. 5. «Сшивание» значений потенциала на границах элементов

Базисные функции как весовые функции

Базисные функции можно представить в виде весовых  функций узловых параметров. Так, на первом элементе при :

.

Заметим, что значение функции u на левом конце элемента не зависит от u₂.

При =1/2:   .

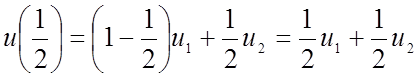Теперь значение u одинаково зависит от u₁, u₂.

При =3/4:    .

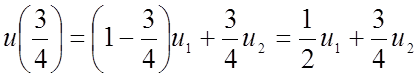Коэффициенты при u₁ и u₂ называются весовыми коэффициентами. В данном случае можно говорить, что значение u зависит от u₂ больше, т.к. больше весовой коэффициент при u₂.

При =1:     .

Здесь значение u на правом конце элемента не зависит от u₁.

Данные весовые функции могут быть рассмотрены как глобальные функции, (см. рис. 6), в которых весовая функция w_n, ассоциируемая с глобальным узлом n, конструируется из базисных функций  элементов, примыкающих к данному узлу.

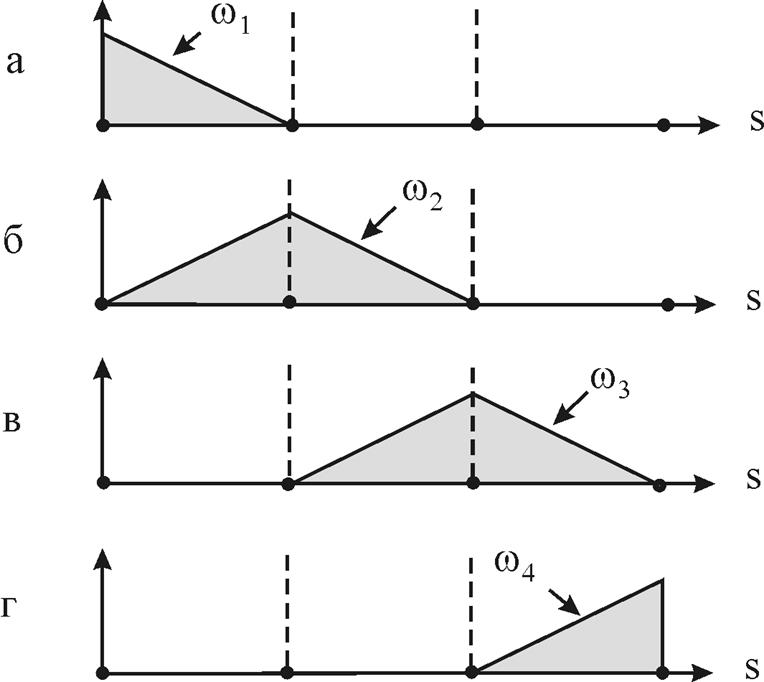
Рис. 6. Весовые функции w_n, ассоциированные